1.最大匹配里的边,每一条边都需要使用顶点覆盖,也就是说最小点覆盖大于等于最大匹配数
2.我们任取一个最大匹配,将在最大匹配内的点染成蓝色,不在最大匹配内的点染成黑色
显然,不可能有边的两个端点都是黑色,也就是说每条边都至少有一个蓝色点.
我们只需选择蓝色点即可,考虑在每条匹配边中只选一个蓝点。
选择蓝点的方法如下:
如果存在一个端点与黑色点直接相连,那么我们选择这个蓝色点,否则随便选择一个点即可,这样我们就构造了一种大小为最大匹配的最小点覆盖。
注意如果存在下面的情况,则我们需要在1--2这条边中同时选择两个蓝色点来盖住黑色点。但下面这种情况是不存在的。
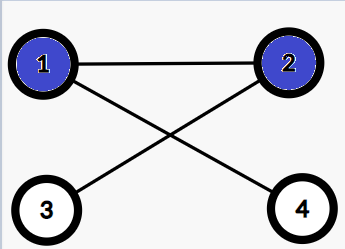
1--2是匹配边,1,2点均是蓝色
3,4都是未匹配点,1-4,2-3是未匹配边
因为如果是这样的话,就会存在增广路。
综上:最小点覆盖=最大匹配
以上构造方式是错误的,某老师的课件上出了错。如下例中,选出1,2,C三个点来进行覆盖,发现2--B这条边盖不住。

首先,因为最大匹配是原二分图边集的一个子集,并且所有边都不相交。
所以至少要从每条匹配边中选出一个端点,于是最小点覆盖包含的点数不可能小于最大匹配包含的边数。于是如果对任意二分图构造一组点覆盖,其包含的点数等于最大匹配,即可证明
构造方法如下:
1:求出最大匹配
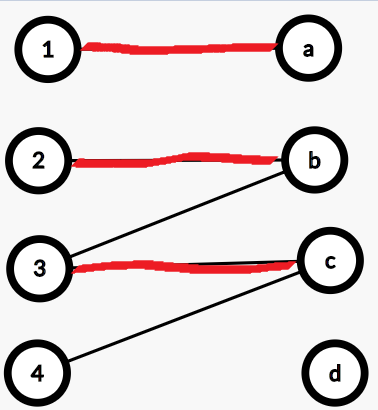
2:从左部每个非匹配点出发,再执行一次DFS找增广路的过程(一定会失败,也就是说走出一条长度为偶数,且非匹配边与匹配边交错的路径),标记所有访问过的节点。下例中红色为匹配边,从未匹配点4出发,走出如下路径(4---C---3---B---2)
3:取左部没有打上标记的点,右边打上标记的点,得到最小点覆盖。下例中取出左部的1号点,右部的C,B两个点。
证明其正确性,经过上述构造方法
1:左边的非匹配点一定都被标记,因为它们是出发点。
2:右边非匹配点一定没有被标记,否则找到增广路
3:一对匹配点要么都被标记,要么没有被标记,因为在在找增广路的过程中,左部匹配点只能通过右部到达(例如上例中c--3这条匹配边,两个点都被标记,A--1这条匹配边,两个点都没有被标记)
在构造中,我们取左部没有被标记的点,右边被标记的点,根据上面讨论可知,正好是每条匹配边取了一个点,于是选出来的点数等于最大匹配的边数。(例如上例中4--C--3--B--2,我们选择了C,B这两个点,当然还有个1号点要取)
再来讨论这种取法是否覆盖了所有的边
1:匹配边一定被覆盖,因为正好有一个端点被取走
2:不存在连接两个非匹配点的边,否则就有长度为1的增广路
3:连接左部非匹配点i,右边匹配点J的边,因为i是出发点,所以j一定被访问,而我们取了右部所有被标记的点,所以这样的边被覆盖
4:连接左部匹配点i,右边非匹配点J的边,,这样的i一定没有被访问,否则再走到J就找到增广路。而我们取了左边所有未被标记的点,于是这样的边也被覆盖。
https://blog.csdn.net/qq_38956769/article/details/80238896