一、满二叉树
定义
满二叉树:一棵高度为h,且含有2^h-1个结点的二叉树称为满二叉树。
简单来说就是树中的每层都含有最多的结点。
特点
满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为2。
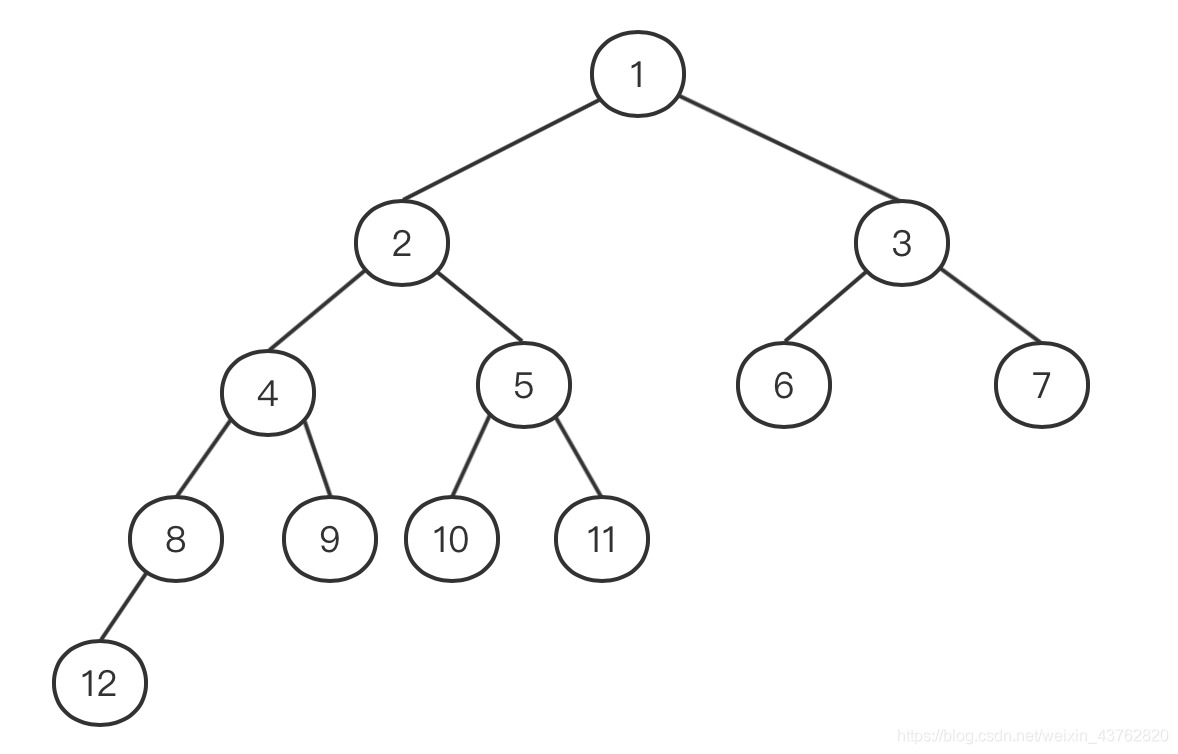
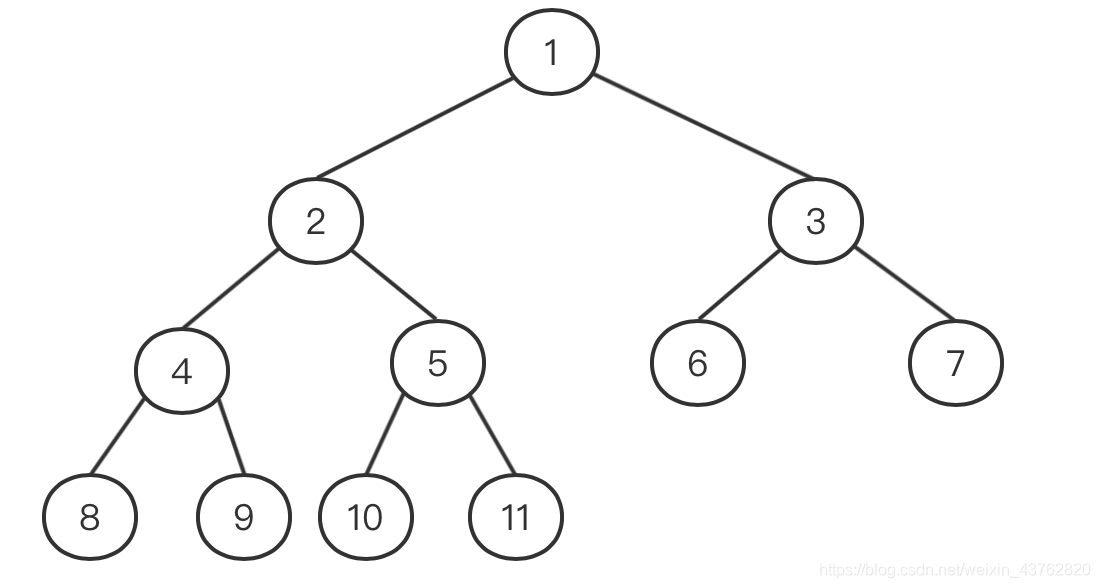
(对满二叉树从上到下,从左到右依次编号,如图)
对于编号为i的结点:
- 若有双亲,双亲节点编号 = ⌊i/2⌋
- 若有左孩子,左孩子编号 = 2*i
- 若有右孩子,右孩子编号 = 2*i + 1
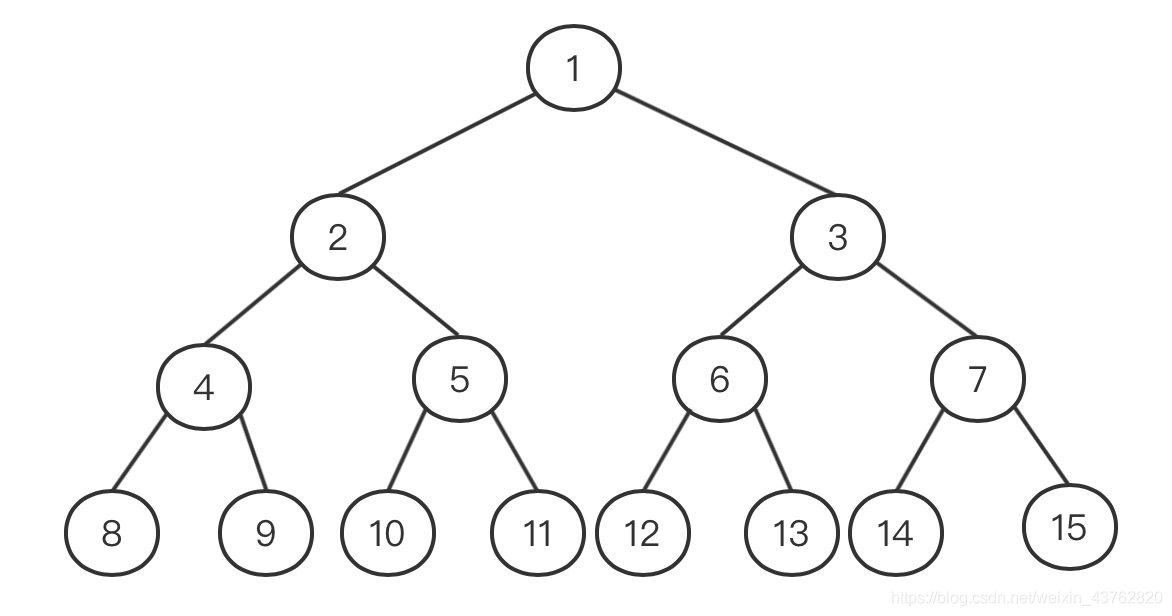
二、完全二叉树
定义
高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
简单来说,就是除了最后一层可以不满(但是必须从左到右),其他层都是满的
特点
- 若i≤⌊n/2⌋ ,则结点i为分支结点,否则为叶子结点。
- 叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层最左边的位置上。
- 若有度为1的结点,则只可能有一个,且该结点只有左孩子而无右孩子(重要特征)。
- 按层序编号后,一旦出现某结点(编号为i)为叶子结点或只有左孩子,则编号大于i的结点均为叶子结点。
- 若n为奇数,则每个分支结点都有左孩子和右孩子;若n为偶数,则编号最大的分支结点(编号为n/2)只有左孩子,没有右孩子,其余分支结点左、右孩子都有。
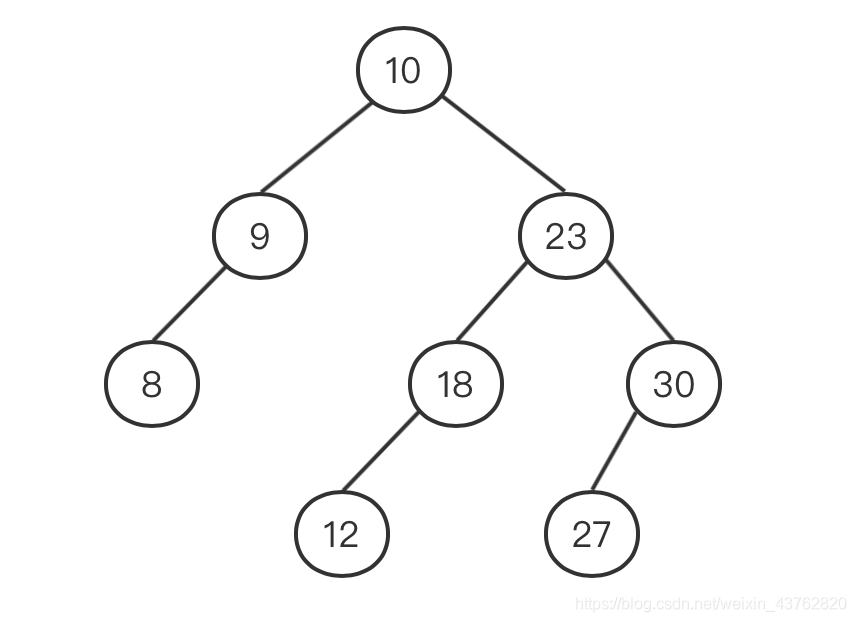
三、二叉排序树
定义
左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字;左子树和右子树又各是一棵二叉排序树
例如,根据序列 10 9 23 18 30 8 12 27 构建一棵二叉排序树:
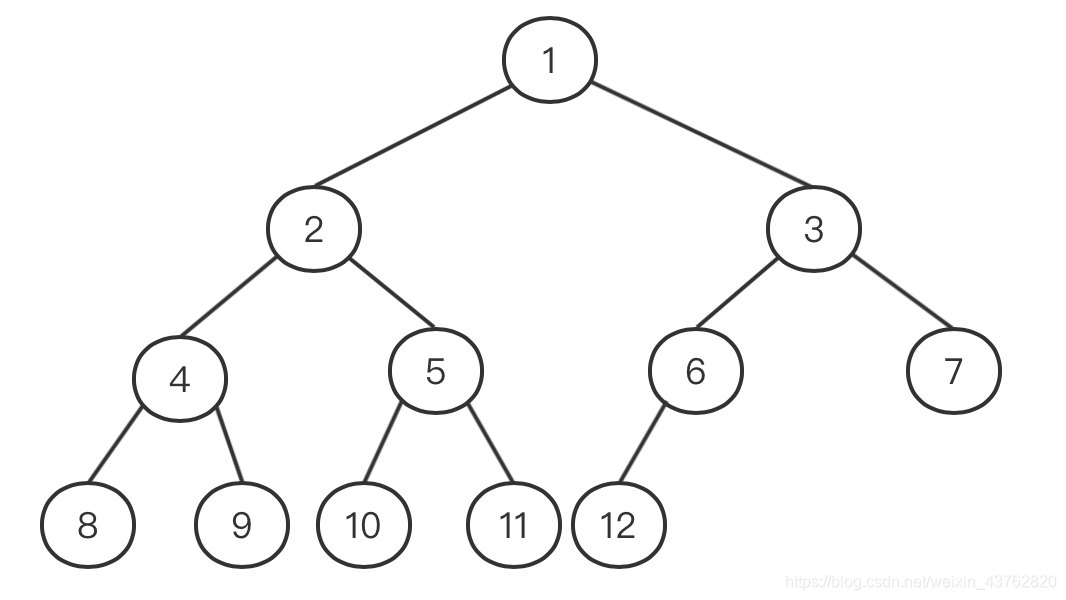
四、平衡二叉树
定义
树上任一结点的左子树和右子树的深度之差不超过1
例如下图,是一棵平衡二叉树:
如果新增一个结点12,就会使得节点1不平衡