CoderForces999E-Reachability from the Capital

E. Reachability from the Capital

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are $n$ cities and $m$ roads in Berland. Each road connects a pair of cities. The roads in Berland are one-way.

What is the minimum number of new roads that need to be built to make all the cities reachable from the capital?

New roads will also be one-way.

Input

The first line of input consists of three integers $n$, $m$ and $s$ ($1\le n\le 5000,0\le m\le 5000,1\le s\le n$) — the number of cities, the number of roads and the index of the capital. Cities are indexed from $1$ to $n$.

The following $m$ lines contain roads: road $i$ is given as a pair of cities $u_i$, $v_i$ ($1\le u_i,v_i\le n$, $u_i\ne v_i$). For each pair of cities $(u,v)$, there can be at most one road from $u$ to $v$. Roads in opposite directions between a pair of cities are allowed (i.e. from $u$ to $v$ and from $v$ to $u$).

Output

Print one integer — the minimum number of extra roads needed to make all the cities reachable from city $s$. If all the cities are already reachable from $s$, print 0.

Examples

input

Copy

9 9 1
1 2
1 3
2 3
1 5
5 6
6 1
1 8
9 8
7 1

output

Copy

3

input

Copy

5 4 5
1 2
2 3
3 4
4 1

output

Copy

1

Note

The first example is illustrated by the following:

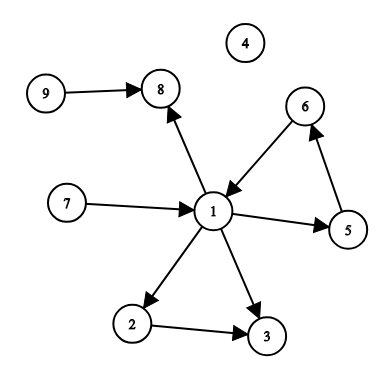
For example, you can add roads ($6,4$), ($7,9$), ($1,7$) to make all the cities reachable from $s=1$.

The second example is illustrated by the following:

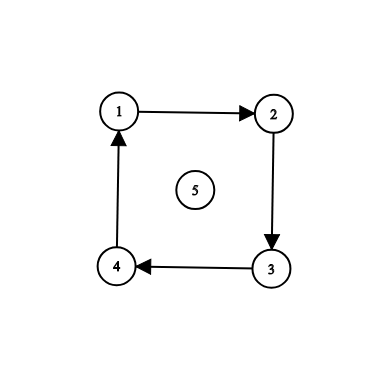
In this example, you can add any one of the roads ($5,1$), ($5,2$), ($5,3$), ($5,4$) to make all the cities reachable from $s=5$.

题意：就是给你很多条路，这些路，城市之间的是无向的，而城市与首都之间的只能由首都到达城市不能由城市到首都。

题解：用到了拓扑图，我们可以把不能通到首都的城市加一条需边使其能到达城市，然后遍历每一条虚边，如果新加的虚边能够使前面加的虚边联通的城市联通，则取消原来的标记。最后标记的数量即为答案；

AC代码为：

#include<bits/stdc++.h>
using namespace std;
const int maxn=5010;
int n,m,k,u,v,tot,cnt;
int first[maxn],vis[maxn],judge[maxn],connect[maxn];


struct Node{
    int to,net;
} node[maxn<<1];


void Init()
{
    tot=1,cnt=0;
    memset(first,-1,sizeof first);
}


void add(int u,int v)
{
    node[tot].to=v;
    node[tot].net=first[u];
    first[u]=tot++; 
}


void dfs(int st)
{
    vis[st]=connect[st]=1;
    for(int e=first[st];e!=-1;e=node[e].net)
    {
        int v=node[e].to;
        if(!vis[v])
        {
            judge[v]=0;
            dfs(v);
        }
    }
}


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>m>>k;
    Init();
    for(int i=0;i<m;i++) 
    {
        cin>>u>>v;
        add(u,v);
    }
    dfs(k);
    memset(vis,0,sizeof vis);
    for(int i=1;i<=n;i++)
    {
        if(!connect[i])
        {
            judge[i]=1;
            dfs(i);
            memset(vis,0,sizeof vis);
        }
    }
    for(int i=1;i<=n;i++) if(judge[i]) cnt++;
    cout<<cnt<<endl;
    return 0;
}