Tinkoff Challenge

C. Mice problem

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Igor the analyst fell asleep on the work and had a strange dream. In the dream his desk was crowded with computer mice, so he bought a mousetrap to catch them.

The desk can be considered as an infinite plane, then the mousetrap is a rectangle which sides are parallel to the axes, and which opposite sides are located in points (x1, y1) and (x2, y2).

Igor wants to catch all mice. Igor has analysed their behavior and discovered that each mouse is moving along a straight line with constant speed, the speed of the i-th mouse is equal to (vix, viy), that means that the x coordinate of the mouse increases by vix units per second, while the y coordinates increases by viy units. The mousetrap is open initially so that the mice are able to move freely on the desk. Igor can close the mousetrap at any moment catching all the mice that are strictly inside the mousetrap.

Igor works a lot, so he is busy in the dream as well, and he asks you to write a program that by given mousetrap's coordinates, the initial coordinates of the mice and their speeds determines the earliest time moment in which he is able to catch all the mice. Please note that Igor can close the mousetrap only once.

Input

The first line contains single integer n (1 ≤ n ≤ 100 000) — the number of computer mice on the desk.

The second line contains four integers x1, y1, x2 and y2 (0 ≤ x1 ≤ x2 ≤ 100 000), (0 ≤ y1 ≤ y2 ≤ 100 000) — the coordinates of the opposite corners of the mousetrap.

The next n lines contain the information about mice.

The i-th of these lines contains four integers rix, riy, vix and viy, (0 ≤ rix, riy ≤ 100 000,  - 100 000 ≤ vix, viy ≤ 100 000), where (rix, riy)is the initial position of the mouse, and (vix, viy) is its speed.

Output

In the only line print minimum possible non-negative number t such that if Igor closes the mousetrap at t seconds from the beginning, then all the mice are strictly inside the mousetrap. If there is no such t, print -1.

Your answer is considered correct if its absolute or relative error doesn't exceed 10 - 6.

Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if .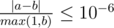

Examples

input

4
7 7 9 8
3 5 7 5
7 5 2 4
3 3 7 8
6 6 3 2

output

0.57142857142857139685

input

4
7 7 9 8
0 3 -5 4
5 0 5 4
9 9 -1 -6
10 5 -7 -10

output

-1

Note

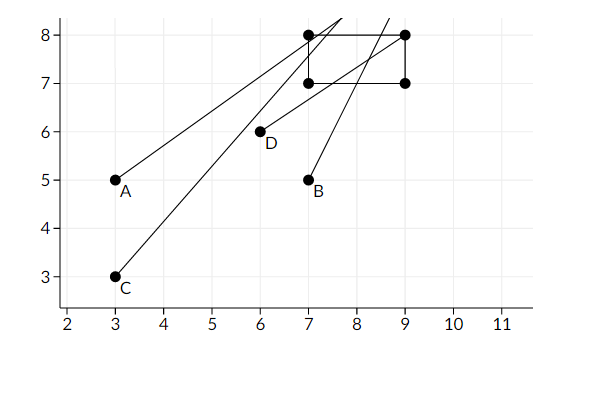
Here is a picture of the first sample

Points A, B, C, D - start mice positions, segments are their paths.

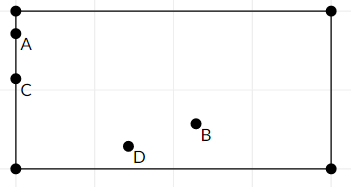
Then, at first time when all mice will be in rectangle it will be looks like this:

Here is a picture of the second sample

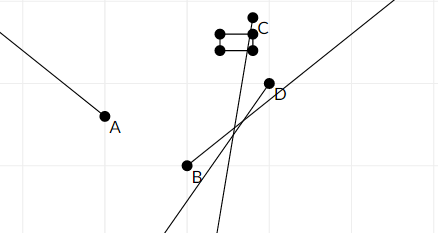
Points A, D, B will never enter rectangle.

题目大意：给你一个捉鼠的矩形区域，有一些老鼠沿着直线运动，问你有没有时间t，这些老鼠同时在这个矩形区域内，输出最小的时间。

题目继续：对于单个直线而言，与矩形的关系，简略而言有下图这么几种。

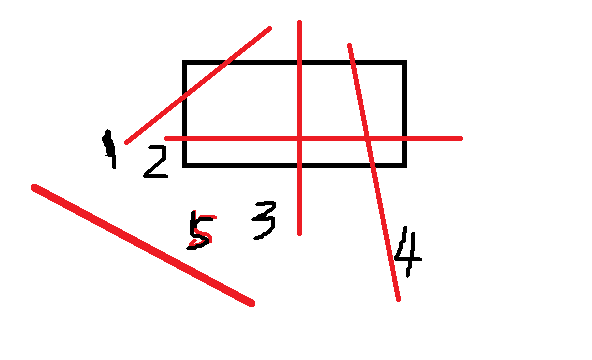
简单举个例子，以直线1而言， 其斜率为正，与矩形的左边和上边相交，其时间区间为[t1, t2]。

t1 = (x1 - x0)/vx, t2 = (y2 - y0)/vy

因此我们找出[l,r]的时间区间，找个最大的l和最小的r，使所有老鼠同时在该矩形区域即可，然后输出l_max。

#include <bits/stdc++.h>

using namespace std;
double x1, x2, y1, y2, x, y, vx, vy;

int main() {
    int n;
    scanf("%d%lf%lf%lf%lf", &n, &x1, &y1, &x2, &y2);
    double Min = 0, Max = 1e18;
    for(int i = 0; i < n; i++) {
        scanf("%lf%lf%lf%lf", &x, &y, &vx, &vy);
        if(vx > 0){
            Min = max(Min, 1.0*(x1 - x)/vx);
            Max = min(Max, 1.0*(x2 - x)/vx);
        }else if(vx < 0){
            Min = max(Min, -1.0*(x - x2)/vx);
            Max = min(Max, -1.0*(x - x1)/vx);
        } else {
            if(x >= x2 || x <= x1) return 0* printf("-1
");
        }
        if(vy > 0){
            Min = max(Min, 1.0*(y1 - y)/vy);
            Max = min(Max, 1.0*(y2 - y)/vy);
        }else if(vy < 0){
            Min = max(Min, -1.0*(y - y2)/vy);
            Max = min(Max, -1.0*(y - y1)/vy);
        } else {
            if(y >= y2 || y <= y1) return 0* printf("-1
");
        }
        if(Max <= Min) return 0*printf("-1
");
    }
    printf("%.9f
", Min);
    return 0;
}