例29 拉丁方阵
问题描述
构造 NXN 阶的拉丁方阵,使方阵中的每一行和每一列中数字1到N只出现一次。如N=4时:
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
输入格式
一个正整数n(2<=n<=9)。
输出格式
生成的n*n阶方阵。
输入样例
4
输出样例
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
(1)编程思路。
观察给出的例子,可以发现:若将每一行中第一列的数字和最后一列的数字连起来构成一个环,则该环正好是由1到N顺序构成;对于第i行,这个环的开始数字为i。按照此规律可以很容易的写出程序。
(2)源程序。
#include <stdio.h>
int main()
{
int n;
scanf("%d",&n);
int i,k,t;
for(i=0; i<n; i++)
{
t=i%n; // 确定该拉丁方阵第i行的第一个元素的值
for(k=0; k<n; k++) // 按照环的形式输出该行中的各个元素
printf("%d ",(k+t)%n+1);
printf(" ");
}
return 0;
}
习题29
29-1 奇数阶魔方
本题选自杭州电子科技大学OJ题库 (http://acm.hdu.edu.cn/showproblem.php?pid=1998)
Problem Description
一个 n 阶方阵的元素是1,2,...,n^2,它的每行,每列和2条对角线上元素的和相等,这样的方阵叫魔方。n为奇数时我们有1种构造方法,叫做“右上方” ,例如下面给出n=3,5,7时的魔方。
3
8 1 6
3 5 7
4 9 2
5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
7
30 39 48 1 10 19 28
38 47 7 9 18 27 29
46 6 8 17 26 35 37
5 14 16 25 34 36 45
13 15 24 33 42 44 4
21 23 32 41 43 3 12
22 31 40 49 2 11 20
第1行中间的数总是1,最后1行中间的数是n^2,他的右边是2,从这三个魔方,你可看出“右上方”是何意。
Input
包含多组数据,首先输入T,表示有T组数据.每组数据1行给出n(3<=n<=19)是奇数。
Output
对于每组数据,输出n阶魔方,每个数占4格,右对齐
Sample Input
2
3
5
Sample Output
8 1 6
3 5 7
4 9 2
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
(1)编程思路。
奇数阶魔方阵采用“右上方”的构造方法为:
首先把1放到顶行的正中间,然后把后继数按顺序放置在右上斜的对角线上,并作如下修改:
1)当到达顶行时,下一个数放到底行,好像它在顶行的上面;
2)当到达最右端列时,下一个数放在最左端列,好像它紧靠在右端列的右方;
3)当到达的位置已经填好数时,或到达右上角的位置时,下一个数就放在刚填写数的位置的正下方。
下面以构造一个3阶魔方阵为例,说明这种方法的构造过程,具体如图1所示。
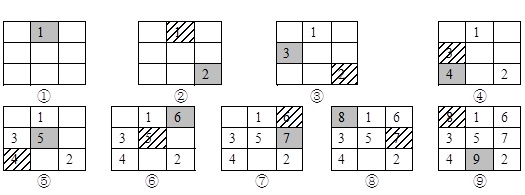
图1 “右上方”连续填数法构造3阶魔方阵
程序中定义一个二维数组a[N][N]来保存方阵,初始时,数组中所有元素均置0。
用变量row和col来存储待填数字num在方阵中的位置,由于第1个数字放在顶行的正中间,因此初始时,行row=0,列col=n/2,待填写数字num=1。
采用“右上方”连续填数法构造方阵的过程是一个循环程序,描述为:
while (待填写数字num<=n*n)
{
确定待填写数字num应该填写的位置row和col;
填写num,即a[row][col]=num;
num++; // 下一个待填写的数字
}
程序中,确定待填写位置的方法是:
1)后继数按顺序放置在右上斜的对角线上,即row--; col++;
2)有三种情形需要调整。
- 当到达顶行时(即row<0), row=n-1;
- 当到达最右端列时(即col==n), col=0;
- 当到达的位置已经填好数时(即(a[row][col]!=0), row+=2; col--;
3)有一种情况,当到达右上角的位置时(row==0 && col==n-1),直接进行特殊处理,row++ 。
(2)源程序。
#include <stdio.h>
int main()
{
int t;
scanf("%d",&t);
while (t--)
{
int a[19][19],row,col,num,n;
scanf("%d",&n);
for (row=0;row<n;row++) // 初始化,数组中所有元素均置0
for (col=0;col<n;col++)
a[row][col]=0;
row=0; col=n/2; num=1;
a[row][col]=num;
while (num<n*n)
{
num++;
if (row==0 && col==n-1) // 到达右上角的位置
row++;
else
{
row--; col++;
if (row<0) row=n-1;
if (col==n) col=0;
if (a[row][col]!=0)
{ row+=2; col--; }
}
a[row][col]=num;
}
for(row=0;row<n;row++)
{
for(col=0;col<n;col++)
printf("%4d",a[row][col]);
printf(" ");
}
}
return 0;
}
29-2 双偶数阶魔方阵
问题描述
当n为双偶数,即n=4*k时,采用双向翻转法构造魔方阵的步骤如下:
(1)将数字1到n*n按由左至右、由上到下的顺序填入方阵中。
(2)将方阵中央部分半数的行中的所有数字左右翻转。
(3)将方阵中央部分半数的列中的所有数字上下翻转。
由于在构造的过程中需要进行两次翻转,因此称为双向翻转法。下面以构造一个4阶魔方阵为例,说明这种方法的构造过程,具体如图2所示。
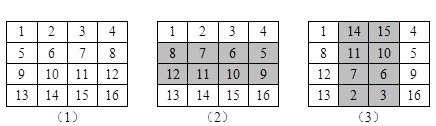
图2 双向翻转法构造4阶魔方阵
输入格式
包含多组数据,首先输入T,表示有T组数据.每组数据1行给出n(4<=n<=20)是4的倍数。
输出格式
对于每组数据,输出n阶魔方,每个数占4格,右对齐
输入样例
2
4
8
输出样例
1 14 15 4
8 11 10 5
12 7 6 9
13 2 3 16
1 2 59 60 61 62 7 8
9 10 51 52 53 54 15 16
24 23 46 45 44 43 18 17
32 31 38 37 36 35 26 25
40 39 30 29 28 27 34 33
48 47 22 21 20 19 42 41
49 50 11 12 13 14 55 56
57 58 3 4 5 6 63 64
(1)编程思路。
程序中定义一个二维数组a[N][N]来保存方阵,构造时,依次进行三个二重循环。
1)将数字1到n*n按由左至右、由上到下的顺序填入方阵中
num=1;
for (row=0; row<n; row++)
for (col=0; col<n; col++)
a[row][col] = num++;
2)将方阵中央部分半数的行中的所有数字左右翻转
对于一个n=4*k阶的双偶数方阵,若按行分成四组的话,每组行号的范围为0~k-1、k~2k-1、2k~3k-1、3k~4k-1,中间有2k行,中间行的行号从k~3k-1,由于k=n/4,所以中间行的行号从n/4~n*3/4-1。
对于每一行,将其中的所有数字左右翻转,实际上就是将一个一维数组逆序排列。因此,第2步的操作可以写成如下的循环:
for (row=n/4; row<=n*3/4-1; row++)
for (col=0; col<n/2; col++)
{
temp = a[row][col];
a[row][col] = a[row][n-1-col];
a[row][n-1-col] = temp;
}
3)将方阵中央部分半数的列中的所有数字上下翻转。
第3步的操作类同于第2步的操作,只是将行列的关系颠倒了,可以写成如下的循环:
for (col=n/4; col<=n*3/4-1; col++)
for (row=0; row<n/2; row++)
{
temp = a[row][col];
a[row][col] = a[n-1-row][col];
a[n-1-row][col] = temp;
}
(2)源程序。
#include <stdio.h>
int main()
{
int t;
scanf("%d",&t);
while (t--)
{
int a[20][20],row,col,num,n,temp;
scanf("%d",&n);
num=1;
for (row=0; row<n; row++)
for (col=0; col<n; col++)
a[row][col] = num++;
for (row=n/4; row<=n*3/4-1; row++)
for (col=0; col<n/2; col++)
{
temp = a[row][col];
a[row][col] = a[row][n-1-col];
a[row][n-1-col] = temp;
}
for (col=n/4; col<=n*3/4-1; col++)
for (row=0; row<n/2; row++)
{
temp = a[row][col];
a[row][col] = a[n-1-row][col];
a[n-1-row][col] = temp;
}
for(row=0;row<n;row++)
{
for(col=0;col<n;col++)
printf("%4d",a[row][col]);
printf(" ");
}
}
return 0;
}
29-3 分数矩阵
问题描述
我们定义如下矩阵:
1/1 1/2 1/3
1/2 1/1 1/2
1/3 1/2 1/1
矩阵对角线上的元素始终是1/1,对角线两边分数的分母逐个递增。
请求出这个矩阵的总和。
输入格式
每行给定整数N (N<50000),表示矩阵为 N*N.当N为0时,输入结束。
输出格式
输出答案,保留2位小数。
输入样例
1
2
3
4
0
输出样例
1.00
3.00
5.67
8.83
(1)编程思路。
题目中的分数矩阵是一个对称矩阵,因此我们可以先计算下三角矩阵的和sum。对角线上有n个1/1,因此对角线的和为n,这样这个分数矩阵的总和为2*sum-n。
下三角矩阵中有n行,第i行有i个数,依次为1/i、1/(i-1)、…、1/2、1/1,因此计算下三角矩阵的和采用简单循环即可完成。
(2)源程序。
#include <stdio.h>
int main()
{
int n,i;
double presum,sum;
while (scanf("%d",&n) && n!=0)
{
presum=1.0;
sum=presum;
for (i=2;i<=n;i++)
{
presum+=1.0/i; // 每行的和 1/i+1/(i-1)+…+1/2+1/1
sum+=presum; // 下三角矩阵中各行和的总和
}
printf("%.2lf ",sum*2-n); // 上下三角阵的和减对角线的和
}
return 0;
}