哈希函数一般都要取模,取模一般都要取质数,那么为什么一定要取质数呢?
做如下分析:
概念与公式
设我们通过哈希函数得到的未取模的值为X,一质数模数为a,非质数模数为b,X对a取模后的结果为Ya,对b取模后的结果为Yb
则有
\[Y_a\equiv X \pmod a \\ Y_b\equiv X\pmod b \\ c(x \; mod \; y)=(cx)\; mod \; (cy)\\ (a+b)\; mod \; p=(a\; mod\; p+b\; mod\; p)\;mod \;p \]以上公式与概念均已被证明,是推论的基石
假设所有X随机出现,则有
- 模质数时:
\[ Y_a \in [0,a-1],均匀分布
\]
- 模合数时:
\[ Y_b \in [0,b-1],均匀分布
\]
假设X成公差为m的等差数列出现,且m与b存在公因数c,则有
- 模质数时:
\[记首项为X_1,第i项为X_i,第i项取模后得到Y_i,则\\ \\
\begin{equation}
\begin{aligned}
Y_i&=(X_1+(i-1)m)\;\textbf{mod}\;a\\
&=(X_1\; \textbf{mod} \; a+((i-1)m)\;\textbf{mod}\;a)\;\textbf{mod}\;a\\
&=(Y_1+k_i)\;\textbf{mod}\;a\qquad\qquad,k_i\in[0,a)
\end{aligned}
\end{equation}
\]
可见仍有
\[ Y_i\in[0,a-1]
\]
- 模合数时:
\[\begin{equation}
\begin{aligned}
Y_i&=(X_1+(i-1)m)\;\textbf{mod}\;b\\
&=(X_i\; \textbf{mod} \; b+((i-1)m)\;\textbf{mod}\;b)\;\textbf{mod}\;b\\\
&=(Y_1+(i-1)(\frac{m}{c})\;\textbf{mod}\;(\frac{b}{c}))\; \textbf{mod} \;b\\
&=(Y_1+k_i)\;\textbf{mod} \;b\qquad\qquad,k_i\in[0,\frac{b}{c})
\end{aligned}
\end{equation}
\]
可见Yi取值范围缩小到了原来的1/c,即成等差数列的X每b/c个数据就会出现一次冲突
以上就是公式推导,下面可以用实验证明一下
数据实验
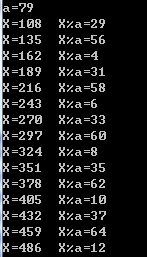
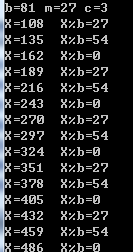
以一组以108为首项,27为公差的等差数列观察,有如下结果:
可以看到,模合数的情况下每3项就会发生一次碰撞,而模质数的情况下没有发生碰撞,这样的例子还有很多,读者可以自行举例实验
总结
之所以要模质数,是因为对于特殊数据,模合数的话会发生大量碰撞,而模质数可以避免这种情况
以上。