1.项目的Github地址
https://github.com/crvz6182/sudoku
2.开发预估耗时:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | |
| · Estimate | · 估计这个任务需要多少时间 | 10 | |
| Development | 开发 | 890 | |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | |
| · Design Spec | · 生成设计文档 | 5 | |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 5 | |
| · Design | · 具体设计 | 20 | |
| · Coding | · 具体编码 | 500 | |
| · Code Review | · 代码复审 | 30 | |
| · Test | · 测试(自我测试,修改代码,提交修改) | 300 | |
| Reporting | 报告 | 95 | |
| · Test Report | · 测试报告 | 60 | |
| · Size Measurement | · 计算工作量 | 5 | |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | |
| 合计 | 995 |
3.解题思路
这次的项目要求既能生成不重复的数独又能解数独。
生成数独算法的灵感来源于《编程之美》中有关数独的一部分论述,书中提到可以通过生成好的3x3矩阵扩展成合法的9x9数独。由于不能重复,随机生成再查重要消耗相当多的时间,而且当时也不知道其他顺序生成的方法,就觉得这个主意不错。
书中的算法虽然不能满足1000000个的需求,但是给出了如何增加变化的提示。可以通过部分行列的对换生成更多种类的数独。在这次题目限制的左上角数字不变的情况下,只要确定了一个3x3矩阵,就可以生成2*6*6*2*6*6=5184个数独。3x3矩阵可以视为生成数独的一个“种子”。接下来就要确保不同的种子生成的数独中没有重复了。
种子和最后生成的数独中的每个3x3区域都是一一对应的。将最后生成的数独中左上角的3x3区域中的格子编号:(左上角固定为6)
| 6 | X | Y |
| x | a | b |
| y | c | d |
由于6不能变换位置,因此行列变换只会涉及第2,3行和2,3列。剩下的数字只能从1,2,3,4,5,7,8,9里选。
以如下顺序填充这个区域:先取一组数X,Y,再取一组数x,y,然后把剩下的数字由大到小填入abcd。只要两个数独中X,Y,x,y这四个位置的数字不完全相同就不会重复。假如数字相同但位置不同,进行行列变换后虽然可以使位置相同,但会影响abcd四个数的位置,因此还是不同情况。在这个规则下生成的种子可以有8*7*6*5=1680个。总共可以生成1680*5184=8709120个,满足1000000个的需求。
解数独采用了比较简单的回溯法,依次往未填入数字的格子中填数,如果无法继续进行则回溯到上一次填数的位置。直到全部填完,或是回溯到开头后发现无解。
4.设计思路
没有使用类,在main函数中判断要解还是生成,以及生成种子。
关于生成的函数:
void transform(int sudoku[][9], int x, int y, int X, int Y, int* others, int num, char *result, int &r_tag)
用于将种子扩展为数独并进行变换,变换后结果输出到result
关于求解的函数:
bool in_area(int sudoku[][9], int x, int y, int i)
判断某个数是否已经在一个3x3区域内
void solve(int sudoku_s[][9], char* result, int &r_tag)
求解一个数独并将结果输出到result
调用关系:
main调用solve,transform
solve调用in_area
关于单元测试:
单元测试针对上述三个函数,给定不同输入情况并判断是否正常输出
(教程中给的单元测试操作方法没有生成.exe,但是覆盖率分析插件只能针对.exe,我尝试了很久也没能一起使用)

5.程序改进
这次的项目可以说有一半的时间都花在了改进上。改进过程中没有改动算法,主要是针对细节问题进行优化。
在第一版完成后,生成的运行速度特别慢。后来通过性能分析发现字符串的“+=”拼接操作占用了大量时间,于是改用字符数组存储最后结果,性能得到了显著提升。在自己的电脑上测试时生成1000000个的所需时间从一分多钟降到了6s左右。
在求解算法中我一开始使用多位数保存所有可能选择,性能分析后发现由于需要多次除法和取余数运算导致效率很低,后来改用了数组进行保存,用时减少了近6/7。
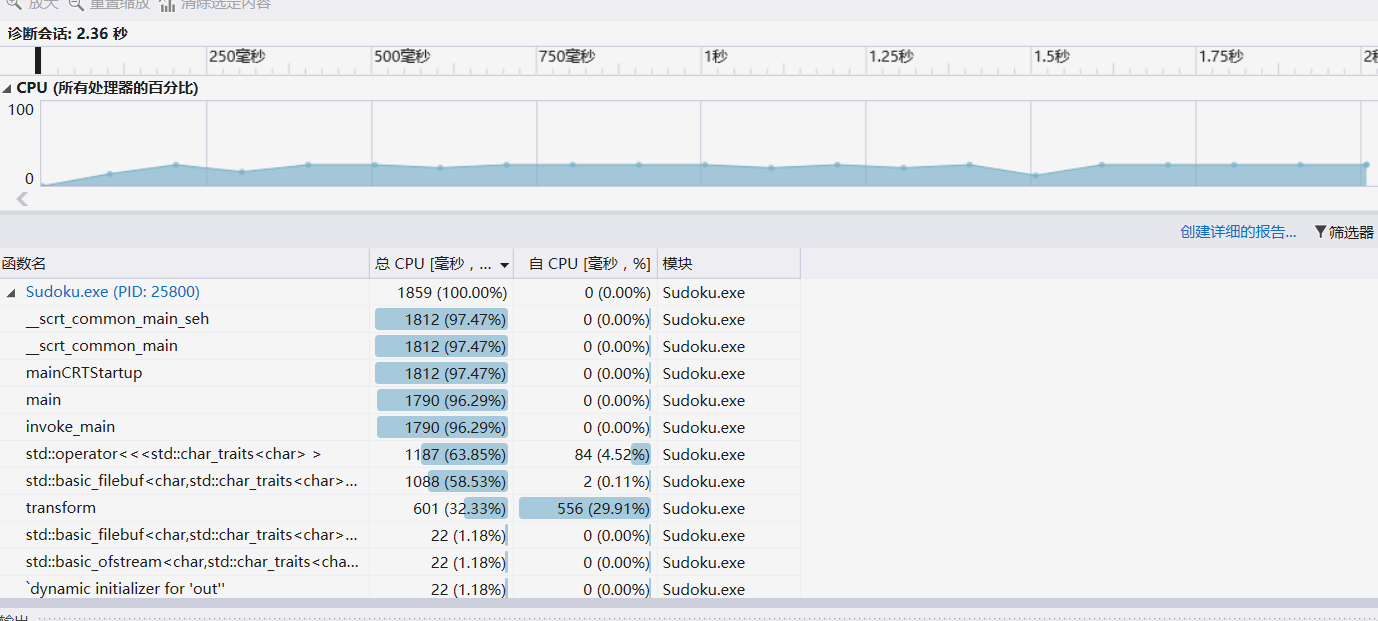
时间还是主要花在对字符的操作上
6.代码展示
for (x = 1; x <= 7; x++) for (y = x + 1; y <= 8; y++) for (X = 1; X <= 7; X++) for (Y = X + 1; Y <= 8; Y++) if (X != x&&X != y&&Y != x&&Y != y) { for (int i = 1; i < 9; i++) { if (X != i&&x != i&&Y != i&&y != i) { if (i == 6) others[j++] = 9; else others[j++] = i; } if (j == 4) { j = 0; break; } } if (X == 6)X = 9; if (Y == 6)Y = 9; if (x == 6)x = 9; if (y == 6)y = 9;
遍历所有种子,用x,y,X,Y保存关键区分元素,others数组保存其他元素
for (x1 = 0; x1 < 2; x1++) { for (x2 = 0; x2 < 6; x2++) { for (x3 = 0; x3 < 6; x3++) { for (y1 = 0; y1 < 2; y1++) { for (y2 = 0; y2 < 6; y2++) { for (y3 = 0; y3 < 6; y3++) { ...... }
遍历所有行列变换的情况,循环内部为根据相应情况进行变换
int x = 0, y = 0, i = 0, j = 0, m = 0, n = 0; for (int p = 0; p < 9; p++) for (int q = 0; q < 9; q++) { if (sudoku[p][q] == 0) list_tag[p][q] = -1; else list_tag[p][q] = -2; for (int r = 0; r < 9; r++) { list[p][q][r] = 0; } } while (x != 9 && y != -1) {//遍历 if (0 <= x&&x <= 8 && 0 <= y&&y <= 8 && sudoku[x][y] == 0) { for (i = 1; i <= 9; i++) { if (in_area(sudoku, x, y, i))continue; for (j = 0; j < 9; j++) { if (sudoku[x][j] == i) break; if (sudoku[j][y] == i) break; } if (j != 9)continue; list[x][y][++list_tag[x][y]] = i; } if (list_tag[x][y] == -1) { st = 1; y--; if (y == -1) { x--; y = 8; } } else { sudoku[x][y] = list[x][y][list_tag[x][y]]; st = 0; y++; if (y == 9) { x++; y = 0; } } } else { if (list_tag[x][y] == -2) { switch (st) { case 0: y++; if (y == 9) { x++; y = 0; }break; case 1: y--; if (y == -1) { x--; y = 8; } break; } } else { if (list_tag[x][y] == 0) { sudoku[x][y] = 0; list[x][y][0] = 0; list_tag[x][y] = -1; st = 1; y--; if (y == -1) { x--; y = 8; } } else { list[x][y][list_tag[x][y]] = 0; sudoku[x][y] = list[x][y][--list_tag[x][y]]; st = 0; y++; if (y == 9) { x++; y = 0; } } } } if (y == -1) { cout << "无解 "; exit(1); } } for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { result[r_tag++] = char(sudoku[i][j] + '0'); if (j == 8) result[r_tag++] = ' '; else result[r_tag++] = ' '; } } result[r_tag++] = ' ';
求解数独时的回溯过程,用数组保存每个位置可以填的所有数字
7.完成后的PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 20 |
| Development | 开发 | 890 | 1400 |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 80 |
| · Design Spec | · 生成设计文档 | 5 | 5 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 5 | 5 |
| · Design | · 具体设计 | 20 | 20 |
| · Coding | · 具体编码 | 500 | 500 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 300 | 600 |
| Reporting | 报告 | 95 | 120 |
| · Test Report | · 测试报告 | 60 | 100 |
| · Size Measurement | · 计算工作量 | 5 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 10 |
| 合计 | 995 | 1470 |
对我来说,这次作业的压力不亚于当初让我忙了好几天的OO出租车作业。要想在时限内尽量完美的完成任务对我来说很难,光是在Debug上我就花了好几个小时,这几天几乎一直都在做相关的事情。所以我最后没有写附加题,没有用DLX算法,编码质量也很差……就个人能力上来说我还很弱,可能选择这门课的目的就是为了锻炼一下自己吧……