[AGC035E] Develop

题目

点这里看题目。

分析

AGC 的难题都很巧妙

对于这种 " 操作 + 计数 " 题目，我们常用方法是分析任意局面可以被操作出来的充要条件。

当然，这也不是一敲脑门就能想出来的

对于这道题，我们不妨考虑删除的先后顺序。比如，如果 (x-2) 最终被删除，那么必然有 (x) 在 (x-2) 之前被删除；同理， (x+k) 在同样条件下有 (x) 在 (x+k) 之前被删除。

因此我们可以对于任意局面，找出其中被删除的集合 (D) 。对于 (xin D) ，由于我们要求 (x-2) 和 (x+k) 在 (x) 之后删除，所以可以连接有向边 (x ightarrow x-2) 和 (x ightarrow x+k) 。此时如果图中出现了圈，那么显然就是不合法的，自己不可能在自己之前删除；反过来，如果不存在圈，那么按照拓扑序进行删除必然是可行的。

因此得到：局面可以被操作当且仅当其对应的图中不存在圈。

由于图本身是静态的，只是 (D) 在变，所以我们可以在图上面决策 (D) 。注意到图的大致形态与 (K) 的奇偶性相关，分类讨论：

• (K) 是偶数，此时图是两个连通块，并且连通块内部为 链 + 反向边 。这种情况就是要求不存在连续的 (K+1) 个点被选，怎么操作都可以。

• (K) 是奇数，此时图为两条链，中间有一些跨链的边。为了图的简洁，我们不妨让一些边平行于边框，这里选择的是奇点指向偶点的边。当 (K=3) 时，下图是一个不错的参考：

  

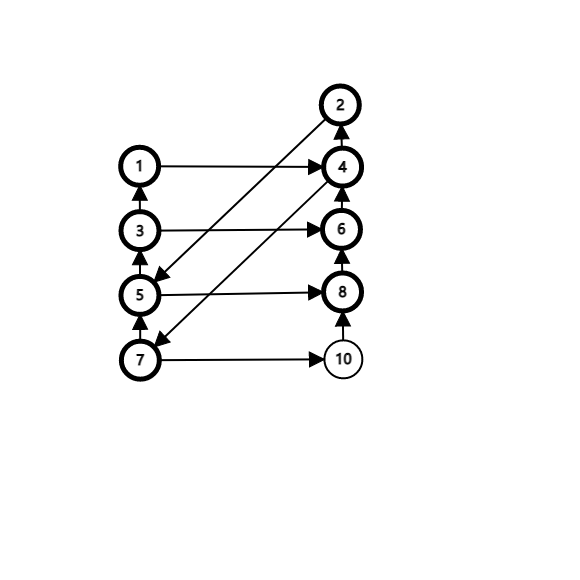
  显然图上最短的环上有 (K+2) 个点，可以表示为： (a ightarrow a-2 ightarrow dots ightarrow b-k ightarrow b ightarrow b-2 ightarrow dots ightarrow a-k) （ (a) 是奇数而 (b) 是偶数 ）。可以发现环的序列按照 向上 + 向右 + 向上 排列；又由于我们的序列必须接到右边的向上部分，因此需要再记录当前右边连续向上的长度。

  于是可以定义 DP 状态如下：

  (f(i,j,k)) ：第 (i) 层，从该层左边出发的序列最长为 (j) ，从该层右边起的连续被选节点有 (k) 个的方案数。

  转移有些细节，建议参考代码。其实转移很简洁，如果你写的很长可以考虑重构

小结：

1. 此类问题的常用转化方法非常重要！
2. 对于环，将其简化拆分成序列的思想也很重要。

代码

#include <cstdio>

#define rep( i, a, b ) for( int (i) = (a) ; (i) <= (b) ; ++ (i) )
#define per( i, a, b ) for( int (i) = (a) ; (i) >= (b) ; -- (i) )

typedef long long LL;

const int MAXN = 155;

template<typename _T>
void read( _T &x )
{
	x = 0; char s = getchar(); int f = 1;
	while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
	while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ); s = getchar(); }
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ) putchar( '-' ), x = -x;
	if( 9 < x ) write( x / 10 );
	putchar( x % 10 + '0' );
}

template<typename _T>
_T MAX( const _T a, const _T b )
{
	return a > b ? a : b;
}

int N, K, mod;

LL Mul( LL x, int v ) { return x * v % mod; }
int Sub( int x, int v ) { return ( x -= v ) < 0 ? x + mod : x; }
int Add( int x, int v ) { return ( x += v ) >= mod ? x - mod : x; }

namespace EvenK
{
	int f[MAXN];
	
	void Solve()
	{
		f[0] = 1, K >>= 1;
		rep( i, 1, N )
		{
			rep( j, MAX( 1, i - K ), i )
				f[i] = Add( f[i], f[j - 1] );
			if( i <= K ) f[i] = Add( f[i], 1 );
		}
		write( Mul( f[N >> 1], f[N + 1 >> 1] ) ), putchar( '
' );
	}
}

namespace OddK
{
	int f[MAXN << 1][MAXN][MAXN];
	
	void Solve()
	{
		f[0][0][0] = 1; int lst = 0;
		for( int i = 2 ; i - K <= N ; i += 2 )
		{
			rep( j, 0, K + 1 ) rep( k, 0, N )
				f[i][0][0] = Add( f[i][0][0], f[i - 2][j][k] );
			//Both Ignored
			if( i <= N )
				rep( j, 0, K + 1 ) rep( k, 0, N )
					f[i][0][k + 1] = Add( f[i][0][k + 1], f[i - 2][j][k] );
			//Left Ignored, Right Chosen
			if( i - K >= 1 )
				rep( k, 0, N )
				{
					rep( j, 1, K ) //Must be connected to the Right, so we don't assume that the transfer is available if j = 0
						f[i][j + 1][0] = Add( f[i][j + 1][0], f[i - 2][j][k] );
					f[i][0][0] = Add( f[i][0][0], f[i - 2][0][k] );
				}
			//Left Chosen, Right Ignored
			if( i <= N && i - K >= 1 )
				rep( k, 0, N )
					for( int j = 0 ; MAX( k + 1, j ) <= K ; j ++ )
						f[i][MAX( k + 2, j + 1 )][k + 1] = Add( f[i][MAX( k + 2, j + 1 )][k + 1], f[i - 2][j][k] );
			//Both Chosen
			lst = i;
		}
		int ans = 0;
		rep( j, 0, K + 1 ) rep( k, 0, N )
			ans = Add( ans, f[lst][j][k] );
		write( ans ), putchar( '
' );
	}
}

int main()
{
	read( N ), read( K ), read( mod );
	if( K % 2 == 0 ) EvenK :: Solve();
	else OddK :: Solve();
	return 0;
}