初步理解一下:对于一组输入,根据这个输入,输出有多种可能性,需要计算每一种输出的可能性,以可能性最大的那个输出作为这个输入对应的输出。
那么,如何来解决这个问题呢?
贝叶斯给出了另一个思路。根据历史记录来进行判断。
思路是这样的:
1、根据贝叶斯公式:P(输出|输入)=P(输入|输出)*P(输出)/P(输入)
2、P(输入)=历史数据中,某个输入占所有样本的比例;
3、P(输出)=历史数据中,某个输出占所有样本的比例;
4、P(输入|输出)=历史数据中,某个输入,在某个输出的数量占所有样本的比例,例如:30岁,男性,中午吃面条,其中【30岁,男性就是输入】,【中午吃面条】就是输出。
一、条件概率的定义与贝叶斯公式

二、朴素贝叶斯分类算法
朴素贝叶斯是一种有监督的分类算法,可以进行二分类,或者多分类。一个数据集实例如下图所示:
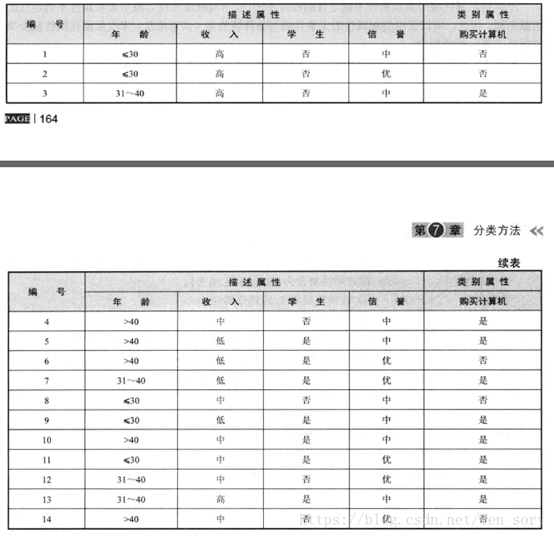
现在有一个新的样本, X = (年龄:<=30, 收入:中, 是否学生:是, 信誉:中),目标是利用朴素贝叶斯分类来进行分类。假设类别为C(c1=是 或 c2=否),那么我们的目标是求出P(c1|X)和P(c2|X),比较谁更大,那么就将X分为某个类。
下面,公式化朴素贝叶斯的分类过程。

三、实例
下面,将下面这个数据集作为训练集,对新的样本X = (年龄:<=30, 收入:中, 是否学生:是, 信誉:中) 作为测试样本,进行分类。
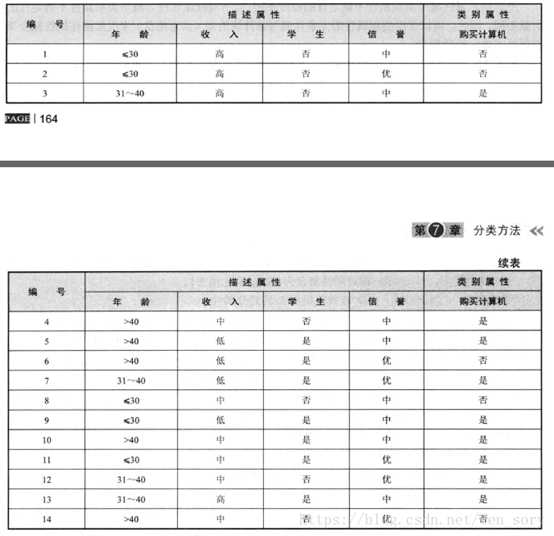
我们可以将这个实例中的描述属性和类别属性,与公式对应起来,然后计算。

参考python实现代码
#coding:utf-8 # 极大似然估计 朴素贝叶斯算法 import pandas as pd import numpy as np class NaiveBayes(object): def getTrainSet(self): dataSet = pd.read_csv('F://aaa.csv') dataSetNP = np.array(dataSet) #将数据由dataframe类型转换为数组类型 trainData = dataSetNP[:,0:dataSetNP.shape[1]-1] #训练数据x1,x2 labels = dataSetNP[:,dataSetNP.shape[1]-1] #训练数据所对应的所属类型Y return trainData, labels def classify(self, trainData, labels, features): #求labels中每个label的先验概率 labels = list(labels) #转换为list类型 labelset = set(labels) P_y = {} #存入label的概率 for label in labelset: P_y[label] = labels.count(label)/float(len(labels)) # p = count(y) / count(Y) print(label,P_y[label]) #求label与feature同时发生的概率 P_xy = {} for y in P_y.keys(): y_index = [i for i, label in enumerate(labels) if label == y] # labels中出现y值的所有数值的下标索引 for j in range(len(features)): # features[0] 在trainData[:,0]中出现的值的所有下标索引 x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]] xy_count = len(set(x_index) & set(y_index)) # set(x_index)&set(y_index)列出两个表相同的元素 pkey = str(features[j]) + '*' + str(y) P_xy[pkey] = xy_count / float(len(labels)) print(pkey,P_xy[pkey]) #求条件概率 P = {} for y in P_y.keys(): for x in features: pkey = str(x) + '|' + str(y) P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y]) #P[X1/Y] = P[X1Y]/P[Y] print(pkey,P[pkey]) #求[2,'S']所属类别 F = {} #[2,'S']属于各个类别的概率 for y in P_y: F[y] = P_y[y] for x in features: F[y] = F[y]*P[str(x)+'|'+str(y)] #P[y/X] = P[X/y]*P[y]/P[X],分母相等,比较分子即可,所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[y] print(str(x),str(y),F[y]) features_label = max(F, key=F.get) #概率最大值对应的类别 return features_label if __name__ == '__main__': nb = NaiveBayes() # 训练数据 trainData, labels = nb.getTrainSet() # x1,x2 features = [8] # 该特征应属于哪一类 result = nb.classify(trainData, labels, features) print(features,'属于',result)
#coding:utf-8 #朴素贝叶斯算法 贝叶斯估计, λ=1 K=2, S=3; λ=1 拉普拉斯平滑 import pandas as pd import numpy as np class NavieBayesB(object): def __init__(self): self.A = 1 # 即λ=1 self.K = 2 self.S = 3 def getTrainSet(self): trainSet = pd.read_csv('F://aaa.csv') trainSetNP = np.array(trainSet) #由dataframe类型转换为数组类型 trainData = trainSetNP[:,0:trainSetNP.shape[1]-1] #训练数据x1,x2 labels = trainSetNP[:,trainSetNP.shape[1]-1] #训练数据所对应的所属类型Y return trainData, labels def classify(self, trainData, labels, features): labels = list(labels) #转换为list类型 #求先验概率 P_y = {} for label in labels: P_y[label] = (labels.count(label) + self.A) / float(len(labels) + self.K*self.A) #求条件概率 P = {} for y in P_y.keys(): y_index = [i for i, label in enumerate(labels) if label == y] # y在labels中的所有下标 y_count = labels.count(y) # y在labels中出现的次数 for j in range(len(features)): pkey = str(features[j]) + '|' + str(y) x_index = [i for i, x in enumerate(trainData[:,j]) if x == features[j]] # x在trainData[:,j]中的所有下标 xy_count = len(set(x_index) & set(y_index)) #x y同时出现的次数 P[pkey] = (xy_count + self.A) / float(y_count + self.S*self.A) #条件概率 #features所属类 F = {} for y in P_y.keys(): F[y] = P_y[y] for x in features: F[y] = F[y] * P[str(x)+'|'+str(y)] features_y = max(F, key=F.get) #概率最大值对应的类别 return features_y if __name__ == '__main__': nb = NavieBayesB() # 训练数据 trainData, labels = nb.getTrainSet() # x1,x2 features = [10] # 该特征应属于哪一类 result = nb.classify(trainData, labels, features) print(features,'属于',result)
参考链接:
https://blog.csdn.net/ten_sory/article/details/81237169