简介
在LeetCode写题目的时候评论区看到一个方法,一开始没看懂,后来查了一些资料整理了一下。原题见文中例3
什么是滑动窗口算法?
The Sliding Problem contains a sliding window which is a sub – list that runs over a Large Array which is an underlying collection of elements.
滑动窗口算法可以用以解决数组/字符串的子元素问题,它可以将嵌套的循环问题,转换为单循环问题,降低时间复杂度。
假设有数组[a b c d e f g h] 一个大小为3的滑动窗口在其上滑动,则有: [a b c] [b c d] [c d e] [d e f] [e f g] [f g h]
算法题例子
例1
给定一个整数数组,计算长度为 'k' 的连续子数组的最大总和。
输入:arr [] = {100,200,300,400} k = 2 输出:700 解释:300 + 400 = 700
思路1:暴力法
没啥好说的,直接遍历,但是时间复杂度很差
C++代码:
int maxSum(int *arr, int length, int k) {
int max = INT32_MIN;
for (int i = 0; i < length - k + 1; i++) {
int tempSum = 0;
for (int j = 0; j < k; j++) {
tempSum += arr[i + j];
}
max = tempSum > max ? tempSum : max;
}
return max;
}
思路2:滑动窗口
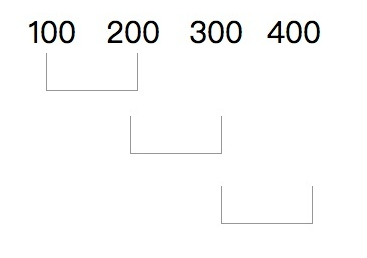
C++代码如下:
int maxSum(int *arr,int length,int k){
int max=0;
for (int i = 0; i < k; ++i) {
max+=arr[i];
} // 初始化max
for (int j = 0; j < length-k; ++j) {
int temp = max-arr[j]+arr[j+k];
max = temp>max?temp:max;
}
return max;
}
例2
给定一个字符串 S 和一个字符串 T,请在 S 中找出包含 T 所有字母的最小子串。(minimum-window-substring)
输入: S = "ADOBECODEBANC", T = "ABC" 输出: "BANC"
思路:左右指针滑动窗口
这个问题让我们无法按照示例 1 中的方法进行查找,因为它不是给定了窗口大小让你找对应的值,而是给定了对应的值,让你找最小的窗口。
我们仍然可以使用滑动窗口算法,只不过需要换一个思路。
既然是找最小的窗口,我们先定义一个最小的窗口,也就是长度为 0 的窗口。

我们比较一下当前窗口在的位置的字母,是否是 T 中的一个字母。
很明显, A 是 ABC 中的一个字母,也就是 T 所有字母的最小子串 可能包含当前位置的 S 的值。
如果包含,我们开始扩大窗口,直到扩大后的窗口能够包含 T 所有字母。

假设题目是 在 S 中找出包含 T 所有字母的第一个子串,我们就已经解决问题了,但是题目是找到最小的子串,就会存在一些问题。
- 当前窗口内可能包含了一个更小的能满足题目的窗口
- 窗口没有滑动到的位置有可能包含了一个更小的能满足题目的窗口
为了解决可能出现的问题,当我们找到第一个满足的窗口后,就从左开始缩小窗口。
- 如果缩小后的窗口仍满足包含 T 所有字母的要求,则当前窗口可能是最小能满足题目的窗口,储存下来之后,继续从左开始缩小窗口。
- 如果缩小后的窗口不能满足包含 T 所有字母的要求,则缩小窗口停止,从右边开始扩大窗口。
缩小窗口停止:

向右扩大停止:

不断重复上面的步骤,直到窗口滑动到最右边,且找不到合适的窗口为止。最小满足的窗口就是我们要找的 S 中包含 T 所有字母的最小子串。

C++代码如下:
string maxSubString(string s,string t){
map<char,int> rightData;
for (int i = 0; i < t.length(); ++i) {
if(rightData.find(t[i])!=rightData.end()){
rightData[t[i]]++;
} else{
rightData[t[i]] = 1;
}
}
int leftPos = 0;
int rightPos = 0;
// 窗口的左右指针
int count = t.length(); // t中不被子串包含的字符数
int min = INT32_MAX; // 最小长度
string res;
while (rightPos < s.length()){
if(rightData.find(s[rightPos])!=rightData.end()){
if(rightData[s[rightPos]]>0)
count--;
rightData[s[rightPos]]--;
}
rightPos++;
while (count==0) { // 找到子串,左边向右收缩
if(rightPos-leftPos<min){
min = rightPos -leftPos;
res = s.substr(leftPos,rightPos-leftPos);
}
if(rightData.find(s[leftPos])!=rightData.end()){
rightData[s[leftPos]]++;
if(rightData[s[leftPos]]>0)
count++;
}
leftPos++;
}
}
return res;
}
在LeetCode评论区看到一个化简后的写法,其实里面的j就是rightPos,i就是leftPos
int lengthOfLongestSubstring(string s) {
int size,i=0,j,k,max=0;
size = s.size();
for(j = 0;j<size;j++){
for(k = i;k<j;k++)
if(s[k]==s[j]){
i = k+1;
break;
}
if(j-i+1 > max)
max = j-i+1;
}
return max;
}
例3
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。(longest-substring-without-repeating-characters)
输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
通过例2,我们发现这种滑动窗口的问题可以用一左一右两个指针来解决。
和例 2 相似,我们不断的扩大/缩小窗口,把无重复字母的窗口大小保存下来,直到窗口滑动结束,就找到了不含有重复字符的 最长子串 的长度。
思路
leftPos 窗口左指针
rightPos 窗口右指针
只要保证窗口内的子串没有重复字符即可,用map来记录
其实这也是遍历一遍所有符合条件的子串的方法,时间复杂度为O(n)
C++代码如下:
int lengthOfLongestSubstring(string str){
map<char,int> strMap;
int leftPos = 0;
int rightPos = 0;
int max = INT32_MIN;
string res;
while (rightPos<str.length()){
if(strMap.find(str[rightPos])==strMap.end()){
strMap[str[rightPos]] = 1;
rightPos++;
} else{
while (leftPos<rightPos){
if(str[leftPos] == str[rightPos]){
strMap.erase(str[leftPos]);
leftPos++;
break;
} else{
strMap.erase(str[leftPos]);
leftPos++;
}
}
}
if(rightPos-leftPos>max){
max = rightPos-leftPos;
res = str.substr(leftPos,max);
}
}
cout<<res<<endl;
return max;
}
例4
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。(find-all-anagrams-in-a-string)
输入: s: "cbaebabacd" p: "abc" 输出: [0, 6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。
与示例 1 类似,我们维护一个长度为 p 的窗口,然后不断往右滑动查找当前窗口是否为 p 的字母异位词。
方法总结:
具体来说:
- 双指针begin,end——记录滑动窗口的左右边界。
- 一个Hash表——记录的t中的所有字符(去重)以及每个字符的出现次数。原因:由于t中可能包含重复字符,那么不仅要依次判断窗口子序列是否包含t中某个字符,还要判断该字符出现的次数是否与在t中相同。既然字符本身和出现次数相关联,那么就可以用一对键值对来表示,所以可使用Hash表来保存t中的字符和出现频率。C++中,我们用unordered_map<char, int> map;
- 一个计数器count,记录t中包含的字符数(去重后),即需要判断是否存在于t的字符。
- 令begin = 0, end = 0;移动右边界,每当发现一个字符存在于t中,递减该字符在Hash表中出现频次,即<key,value>中value的值,递减至0时,说明该窗口子序列中至少包含了与t中相同个数的该字符,那么此时递减count计数器,表示该字符的判断已完成,需要判断的字符数-1.
- 以此类推,不断拓展右边界,直至count为0,表示窗口序列中已经至少包含了t中所有字符(包括重复的)。
- 分析此时的窗口子序列,t是该序列的子集,条件2已满足。如果两者长度相同,即满足条件3,那么它的左边界begin就是我们想要的结果之一了。但我们不会一直那么幸运,这时就需要收缩窗口的左边界,即end不动,begin向右移动遍历该子序列,直至找到t中包含的字符,此时再次计算end-begin的值,与t长度比较,判断是否是想要的结果。而找到上述字符后,字符频次加1,如加1后该字符频次仍小于0,说明该字符有冗余,而出现频次大于0,则count加1,这是告诉我们有一个字符需要重新被判断了,因为无论它是不是我们想要的,都不能再用了,需要继续向右拓展窗口从新找起。
- 当count != 0时,继续向右拓展窗口,直至count为0,然后判断条件3的同时,向右移动begin遍历子序列,直至count != 0,以此类推。