最小生成树一般有两个算法
- Prim算法
- Kruskal算法
二者都用了贪心的思想
简单来说,把一个图的边都去掉
Prim算法就是不断增大连通分量
Kruskal算法就是不断加边
Prim算法
算法简单描述
-
输入:一个加权连通图,其中顶点集合为V,边集合为E;
-
初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
-
重复下列操作,直到Vnew = V:
-
在集合E中选取权值最小的边<u, v>,其中u为集合Vnew 中的元素,而v不在Vnew 集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
-
将v加入集合Vnew 中,将<u, v>边加入集合Enew 中,将v和<u,v>从V,E集合中删除;
-
简单来说
- 就是把一张有权图的边统统忽略掉,先选择一个顶点作为起始点
- 选择与这个顶点相连的权重最小的边,构成一个连通子图
- 随后不断找为选择过的点,扩大这个连通子图,就能满足连通且权重最小啦
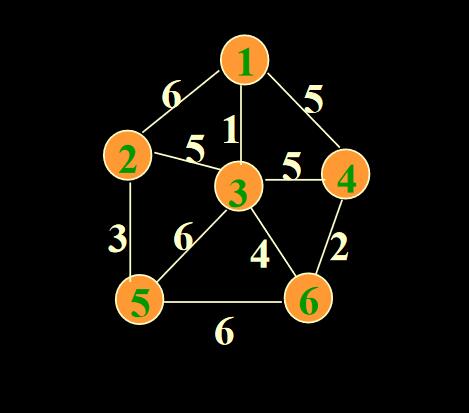
例子
举一个例子
| STEP | 图示 |
|---|---|
| 1、2 | |
| 3、4 | |
| 5 |
算法优化与具体实现
可以发现,在上述例子中有很多重复的操作,比如有一些边在每次加点的时候都要搜索一次。
所以,在实现的时候我们new了两个数组来把复杂度从O(n3)降低到O(n2)
-
lowcost[] 存放生成树顶点集合内顶点到生成树外各顶点的边上的当前最小权值;
-
nearvex[] 记录生成树顶点集合外各顶点,距离集合内那个顶点最近。-1表示已加入生成树。
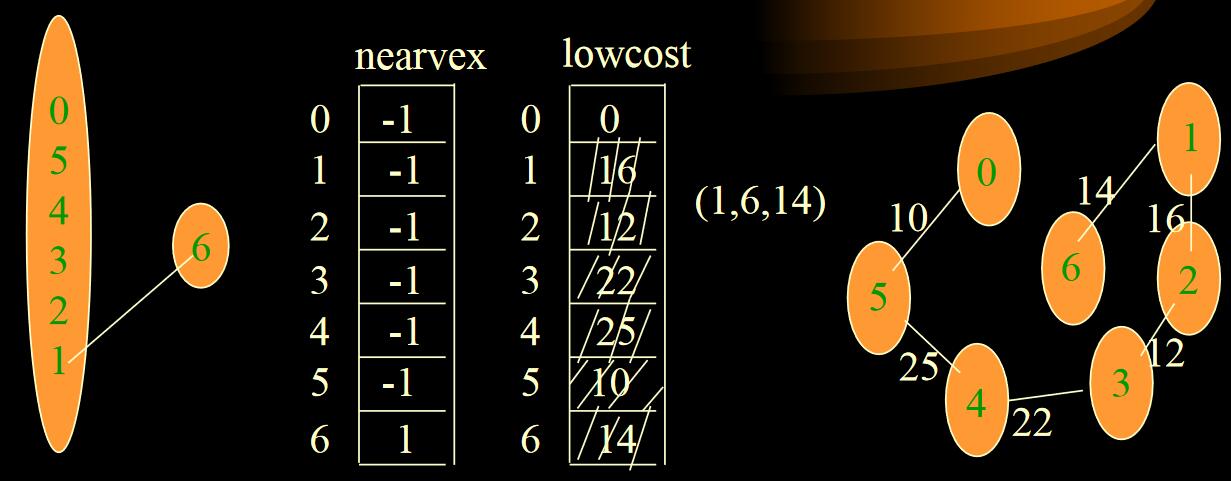
反复做以下工作:
- 在Lowcost[]中选择nearvex[i]!=-1,且lowcost[i] 最小的边用v标记它,则选中的权值最小的边为(nearvex[v],v), 相应的权值为lowcost[v]。
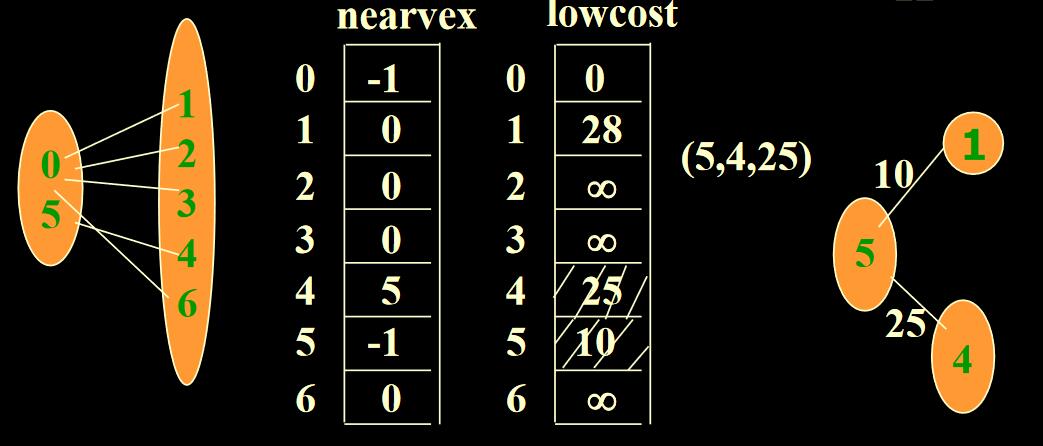
例如在上面图中第一次选中的v=5;则边(0,5),是选中的权值最小的边,相应的权值为lowcost[5]=10
将nearvex[v] 改为-1,表示它已加入生成树顶点集合。将边(nearvex[v],v,lowcost[v])加入生成树的边集合
修改。取lowcost[i]=min{lowcost[i],Edge[v][i]},即用生成树顶点集合外各顶点i到刚加入该集合的新顶点v的距离(Edge[v][i])与原来它所到生成树顶点集合中顶点的最短距离lowcost[i]做比较,取距离近的,作为这些集合外顶点到生成树顶点集合内顶点的最短距离。
如果生成树顶点集合外的顶点i到刚加入该集合新顶点v的距离比原来它到生成树顶点集合中顶点的最短距离还要近,则修改nearvex[i]:
nearvex[i]=v表示生成树外顶点i到生成树的内顶点v 当前距离最短。
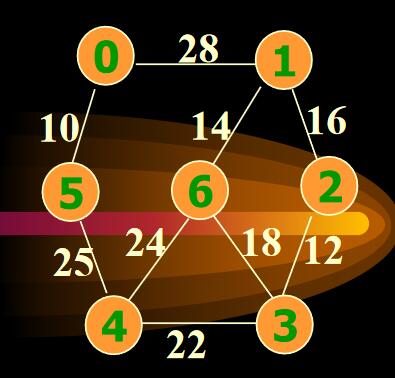
举另外一个例子
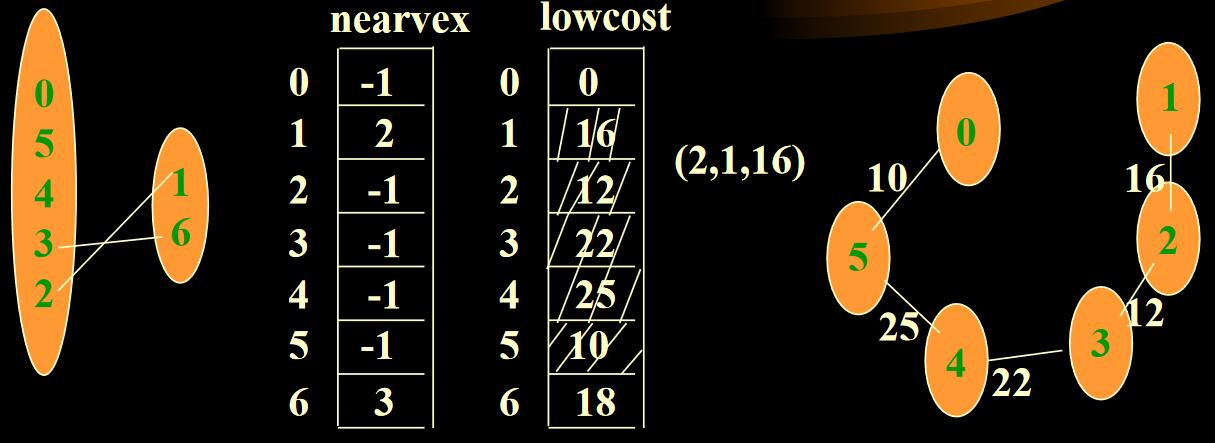
| 图例 | 操作 |
|---|---|
 |
从0开始,把5加入连通分量中。并更新lowcost[4],更新nearvex[5]为-1。 |
 |
把4加入连通分量中。并更新lowcost[6],lowcost[4],更新nearvex[4]为-1。 |
 |
以此类推 |
 |
以此类推 |
 |
以此类推 |
 |
以此类推 |
JAVA 实现
注意,该算法需要使用到,数据结构与算法笔记:图的基础与JAVA实现中实现的图。
public class Prim {
private static final int INF = 999999;
public static int prim(Graph graph) { // 返回权值,并输出过程
int sum_weight= 0 ;
int[] nearvex = new int[graph.getSize() + 1];
int[] lowcost = new int[graph.getSize() + 1];
int numVex = graph.getSize();
for (int i = 1; i < numVex + 1; i++) {
nearvex[i] = 1;
lowcost[i] = INF;
}
// 做第一个点
System.out.println("start at 1");
int v1 = graph.getFirstNeighbor(1);
while (v1 != -1) {
lowcost[v1] = graph.getWeight(1, v1);
v1 = graph.getNextNeighbor(1, v1);
}
nearvex[1] = -1;
// 开始做剩下n-1个点
for (int i = 1; i < numVex; i++) {
int min = INF;
int v = 1;
for (int j = 1; j < numVex + 1; j++) {
// 选择权最小的非连通点
if (nearvex[j] != -1 && lowcost[j] < min) {
v = j;
min = lowcost[j];
}
}
// 处理该点
System.out.println(v + " from " + nearvex[v]+" weight "+lowcost[v]);
sum_weight += lowcost[v];
// 更新表信息
nearvex[v] = -1;
v1 = graph.getFirstNeighbor(v);
while (v1 != -1) {
int weight = graph.getWeight(v, v1);
if (nearvex[v1] != -1 && weight < lowcost[v1]) {
lowcost[v1] = weight;
nearvex[v1] = v;
}
v1 = graph.getNextNeighbor(v, v1);
}
}
return sum_weight;
}
}
最后附上上面两个例子的main函数。
public static void main(String[] args) {
Graph graph1 = new MatrixGraph(GraphType.NoDirectionWeight, 7);
graph1.insertEdge(1, 2, 16);
graph1.insertEdge(3, 2, 12);
graph1.insertEdge(3, 6, 18);
graph1.insertEdge(1, 6, 14);
graph1.insertEdge(4, 6, 24);
graph1.insertEdge(4, 3, 22);
graph1.insertEdge(4, 5, 25);
graph1.insertEdge(7, 5, 10);
graph1.insertEdge(7, 1, 28);
Graph graph2 = new LinkGraph(GraphType.NoDirectionWeight,6);
graph2.insertEdge(1,2,6);
graph2.insertEdge(1,4,5);
graph2.insertEdge(1,3,1);
graph2.insertEdge(2,3,5);
graph2.insertEdge(4,3,5);
graph2.insertEdge(4,6,2);
graph2.insertEdge(3,6,4);
graph2.insertEdge(3,5,6);
graph2.insertEdge(6,5,6);
graph2.insertEdge(2,5,3);
System.out.println(Prim.prim(graph2));
System.out.println(Prim.prim(graph1));
}
输出为
start at 1
3 from 1 weight 1
6 from 3 weight 4
4 from 6 weight 2
2 from 3 weight 5
5 from 2 weight 3
15
start at 1
6 from 1 weight 14
2 from 1 weight 16
3 from 2 weight 12
4 from 3 weight 22
5 from 4 weight 25
7 from 5 weight 10
99
Kruskal算法
算法简单描述
克鲁斯卡尔(Kruskal)算法,是用来求加权连通图的最小生成树的算法。
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。
具体做法:首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止。
例子
举一个例子

算法具体实现
-
所需知识:
-
最小优先队列(堆)
首先要有一个边的最小堆,方便从图中不断找出最小的边
注:实现附于文末
-
并查集(DisjointSet)
并查集的作用是用于快速判断所选边的两个邻接顶点是否已经连通
若已经连通,即disjSet.find(v) == disjSet.find(u),则该弃用改变,转寻接下来最小的边
-
JAVA实现
import chapter6_priorityQueue.MinHeap;
import chapter7_disjointSet.DisjointSet;
public class Kruskal {
private static MinHeap readGraphIntoHeap(Graph graph){
int size = graph.getSize();
MinHeap minHeap = new MinHeap(graph.getEdgeSize());
for (int i = 1; i < size+1; i++) {
int v = graph.getFirstNeighbor(i);
while (v!=-1){
if(v>i) // 防止重复加边
minHeap.insert(new Edge(i,v,graph.getWeight(i,v)));
v = graph.getNextNeighbor(i,v);
}
}
return minHeap;
}
public static int kruskal(Graph graph){
int sum_weight = 0;
int size = graph.getSize();
MinHeap minHeap = readGraphIntoHeap(graph);
int edgesAccpted = 0;
DisjointSet disjSet = new DisjointSet(size);
while (edgesAccpted<size-1){
Edge e = (Edge)minHeap.deleteMin();
int u = e.fromVex;
int v = e.endVex;
if(disjSet.find(v)!= disjSet.find(u)){
edgesAccpted++;
disjSet.union(u,v);
sum_weight+=e.weight;
System.out.println(u+ " from "+v+" weight "+e.weight);
}
}
return sum_weight;
}
}
并附上上述例子的测试
public static void main(String[] args) {
Graph graph1 = new MatrixGraph(GraphType.NoDirectionWeight,5);
graph1.insertEdge(1,2,2);
graph1.insertEdge(1,4,10);
graph1.insertEdge(1,3,12);
graph1.insertEdge(2,3,8);
graph1.insertEdge(2,5,9);
graph1.insertEdge(3,4,6);
graph1.insertEdge(3,5,3);
graph1.insertEdge(4,5,7);
System.out.println(Kruskal.kruskal(graph1));
}
输出结果为
1 from 2 weight 2
3 from 5 weight 3
3 from 4 weight 6
2 from 3 weight 8
19
附录:优先队列MinHeap最小堆
注:仅基本功能,初始化类时需给定size,无自动扩展功能
public class MinHeap {
Comparable[] data; // 第0位不存
private static final int DEFAULT_SIZE = 10;
int current_size;
public MinHeap(int size) {
data = new Comparable[size + 1];
current_size = 0;
}
public MinHeap() {
this(DEFAULT_SIZE);
current_size = 0;
}
public MinHeap(Comparable[] array) {
data = new Comparable[array.length+1];
current_size = array.length;
for (int i = 0; i < array.length; i++) {
data[i+1] = array[i];
}
System.out.println("before");
printHeap();
reSortHeap();
}
public boolean isEmpty() {
return current_size == 0;
}
public boolean isFull() {
return current_size == data.length;
}
public void makeEmpty() {
current_size = 0;
}
private void reSortHeap(){
for (int i = current_size/2; i > 0 ; i--) {
percolateDown(i);
}
}
public void insert(Comparable x){
if(isFull()){
enlargeArray();
}
int hole = ++current_size;
data[hole] = x;
percolateUp(hole);
}
public Comparable deleteMin(){
Comparable t = data[1];
data[1] = data[current_size--];
percolateDown(1);
return t;
}
// 下滤
private void percolateDown(int hole) {
int child ;
Comparable x = data[hole];
for(;hole*2<=current_size;hole=child){
child = hole*2;
if(child+1<=current_size&&data[child].compareTo(data[child+1])>0)
child+=1;
if(x.compareTo(data[child])>0)
data[hole] = data[child];
else
break;
}
data[hole] = x;
}
// 上滤
private void percolateUp(int hole){
Comparable x = data[hole];
for (data[0]=data[hole];x.compareTo(data[hole/2])<0;hole/=2){
data[hole] = data[hole/2];
}
data[hole] = x;
}
private void enlargeArray() {
int size = data.length*2;
Comparable[] nd = new Comparable[size];
for (int i = 0; i < data.length; i++) {
nd[i] = data[i];
}
data = nd;
}
public void printHeap(){
if(isEmpty())
System.out.println("Empty!");
else {
System.out.println("root"+data[1]);
printHeap(1,2);
}
}
private void printHeap(int blank,int index){
if(index<=current_size) {
for (int i = 0; i < blank; i++) {
System.out.print(" ");
}
System.out.println("|------"+data[index]);
printHeap(blank+1,index*2);
}
if(++index<=current_size){
for (int i = 0; i < blank; i++) {
System.out.print(" ");
}
System.out.println("|------"+data[index]);
printHeap(blank+1,index*2);
}
}
}