数据结构与算法笔记：图的基础与JAVA实现

图是由顶点集（VertexSet）和边集（EdgeSet）组成，针对图G，顶点集和边集分别记为V(G)和E(G)。

依据图的边集是否为有向，可把图分为有向图和无向图

根据图是否有权重，可以分为有权图和无权图。

public interface Graph {
    boolean insertEdge(int v1,int v2,int weight);
    boolean deleteEdge(int v1,int v2);
    int getDegree(int v);
    int getInDegree(int v);
    int getOutDegree(int v);
    String depthFirstSearch(int v);
    String breathFirstSearch(int v);
    GraphType getGraphType();
    int getFirstNeighbor(int v); // none return -1
    int getNextNeighbor(int v,int v2); // none return -1
    int getSize();
    int getWeight(int v1,int v2);
    int getEdgeSize();
}

图的基本知识

图的概念

图是由顶点集（VertexSet）和边集（EdgeSet）组成，针对图G，顶点集和边集分别记为V(G)和E(G)。

依据图的边集是否为有向，可把图分为有向图和无向图

根据图是否有权重，可以分为有权图和无权图。

图的基本术语：

1. 邻接点：在一个无向图中，若存在一条边（Vi，Vj），则称Vi，Vj为此边的两个端点，并称它们互为邻接点

2. 出/入边：在一个有向图张，若存在一条边<Vi，Vj>，则称此边为顶点Vi的出边，顶点Vj的一条入边；

3. 度/入度/出度：无向图中的度定义为以该顶点为一个端点的边的数目，记为D(V)。有向图的入度定义为多少边指向该顶点，出度是该顶点出边的个数；

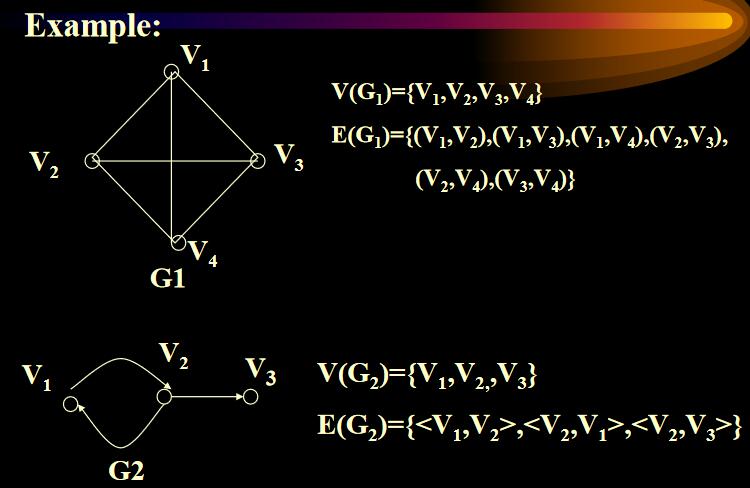
注意：这里不考虑自环和多重边

图的表示方式

图的表示方式有两种：

• 二维数组表示（邻接矩阵）
• 链表表示（邻接表）

（1）邻接矩阵表示（Adjacency Matrix）

在无向图中，邻接矩阵是对称的；

在无权图中，用0表示边<i,j>是不连接的，用1表示边<i,j>是连接的；

在有权图中，用INF表示边<i,j>是不连接的，用weight表示边<i,j>是连接的；

图的类型	示例
无向无权图
有向无权图
有向有权图

（2）邻接表表示（Linked-adjacency Lists）

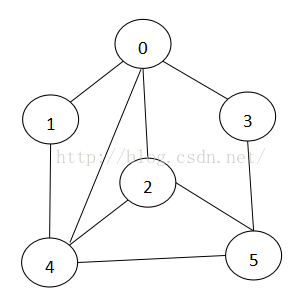
邻接矩阵与邻接表相比，它会造成空间的一定损失，它需要为每个顶点都分配n个边的空间，其实有很多边都是不存在边，但是邻接表的实现就不一样，它只关心存在的边，不关心不存在的边。邻接表由数组+链表组成对于上面的无向图，邻接表表示为（由于有向和无向的差别不是太大，所以只是画出了无向的邻接表表示）：

图	邻接表

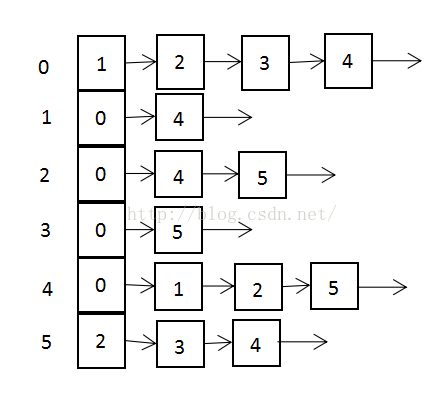注：若要表示有权图，将邻接表的节点数据结构中增加一个weight数据即可

图的JAVA实现

本程序只实现了基本功能，即节点表示为1,2,..,n，暂不支持泛型与删节点

图的类型

图有四种类型

• 有向有权图
• 无向有权图
• 有向无权图
• 无向无权图

public enum GraphType {
    DirectionWeight,
    NoDirectionWeight,
    DirectionNoWeight,
    NoDirectionNoWeight;
}

图的接口类

定义一个图的接口类，如下：

public interface Graph {
    boolean insertEdge(int v1,int v2,int weight);
    boolean deleteEdge(int v1,int v2);
    int getDegree(int v);
    int getInDegree(int v);
    int getOutDegree(int v);
    String depthFirstSearch(int v);
    String breathFirstSearch(int v);
    GraphType getGraphType();
    int getFirstNeighbor(int v); // none return -1
    int getNextNeighbor(int v,int v2); // none return -1
    int getSize();
    int getWeight(int v1,int v2);
    int getEdgeSize();
}

本程序只实现了基本功能，即节点表示为1,2,..,n，暂不支持泛型与删节点

具体实现

（1）LinkGraph类与MatrixGraph类

顾名思义，用邻接表与邻接矩阵实现图。

实现了Graph接口，成员变量与构造函数如下：

public class LinkGraph implements Graph {
    
    private LinkedList<VertexNode>[] vexList;
    private int edgeSize; // 已有边数
    private GraphType type;
    private int maxVertex; // 顶点最大个数
    private static final int INF = 999999; // 用于有权图的无边表示
    Iterator<VertexNode> temp; // 用于缓存getNeighbor方法的Iterator

    public LinkGraph(GraphType type, int size) {
        vexList = new LinkedList[size + 1];
        for (int i = 1; i < size + 1; i++) {
            vexList[i] = new LinkedList();
        }
        maxVertex = size;
        edgeSize = 0;
        this.type = type;
    }
    
    private class VertexNode { // 邻接表节点的内部类
        int vertex;
        int weight;
        VertexNode(int vex, int weight) {
            vertex = vex;
            this.weight = weight;
        }
        VertexNode(int vex) {
            vertex = vex;
            this.weight = 1;
        }
    }

public class MatrixGraph implements Graph {

    private int[][] matrix;
    private int edgeSize; // 已有边数
    private GraphType type;
    private int maxVertex; // 顶点最大个数
    private static final int INF = 999999; // 用于有权图的无边表示

    public MatrixGraph(GraphType type, int size) {
        matrix = new int[size + 1][size + 1];
        maxVertex = size;
        edgeSize = 0;
        this.type = type;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 0; i < size + 1; i++) {
                    for (int j = 0; j < size + 1; j++) {
                        matrix[i][j] = INF;
                    }
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 0; i < size + 1; i++) {
                    for (int j = 0; j < size + 1; j++) {
                        matrix[i][j] = 0;
                    }
                }
                break;
        }
    }

注意用邻接矩阵实现时，因为图的类型不同导致的表示不同，常需要先判断，后进行操作。

（2）insertEdge方法与deleteEdge方法

    boolean insertEdge(int v1,int v2,int weight);
    boolean deleteEdge(int v1,int v2);

这里需要注意的地方是加边和删边的时候要修改edgeSize变量，所以需要一些判断语句

在无权图中，无论weight为多少我们都把他当作1

邻接表实现

    @Override
    public boolean insertEdge(int v1, int v2, int weight) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        boolean contain = false;
        switch (type) {
            case DirectionNoWeight:
                weight = 1;
            case DirectionWeight:
                for (VertexNode vex : vexList[v1]) {
                    if (vex.vertex == v2)
                        contain = true;
                }
                if (!contain)
                    edgeSize++;
                vexList[v1].add(new VertexNode(v2, weight));
                break;
            case NoDirectionNoWeight:
                weight = 1;
            case NoDirectionWeight:
                for (VertexNode vex : vexList[v1]) {
                    if (vex.vertex == v2)
                        contain = true;
                }
                if (!contain)
                    edgeSize++;
                vexList[v1].add(new VertexNode(v2, weight));
                vexList[v2].add(new VertexNode(v1, weight));
                break;
        }
        return true;
    }


    @Override
    public boolean deleteEdge(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        Iterator<VertexNode> iterator;
        switch (type) {
            case DirectionNoWeight:
            case DirectionWeight:
                iterator = vexList[v1].listIterator(0);
                while (iterator.hasNext()) {
                    if (iterator.next().vertex == v2) {
                        iterator.remove();
                        edgeSize--;
                        break;
                    }
                }
                break;
            case NoDirectionWeight:
            case NoDirectionNoWeight:
                iterator = vexList[v1].listIterator(0);
                while (iterator.hasNext()) {
                    if (iterator.next().vertex == v2) {
                        iterator.remove();
                        edgeSize--;
                        iterator = vexList[v2].listIterator(0);
                        while (iterator.hasNext()) {
                            if (iterator.next().vertex == v1) {
                                iterator.remove();
                                edgeSize--;
                                break;
                            }
                            break;
                        }
                    }
                    break;
                }
        }
        return true;
    }

值得注意的是邻接表实现中我们加入的是内部类（VertexNode）作为节点，因此在遍历的时候用到了链表的Iterator

邻接矩阵实现

  @Override
    public boolean insertEdge(int v1, int v2, int weight) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        switch (type) {
            case DirectionNoWeight:
                if (matrix[v1][v2] == 0)
                    edgeSize++;
                matrix[v1][v2] = 1;
                break;
            case NoDirectionNoWeight:
                if (matrix[v1][v2] == 0)
                    edgeSize++;
                matrix[v1][v2] = 1;
                matrix[v2][v1] = 1;
                break;
            case DirectionWeight:
                if (matrix[v1][v2] == INF)
                    edgeSize++;
                matrix[v1][v2] = weight;
                break;
            case NoDirectionWeight:
                if (matrix[v1][v2] == INF)
                    edgeSize++;
                matrix[v1][v2] = weight;
                matrix[v2][v1] = weight;
                break;
        }
        return true;
    }

    @Override
    public boolean deleteEdge(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        switch (type) {
            case DirectionNoWeight:
                if (matrix[v1][v2] != 0)
                    edgeSize--;
                matrix[v1][v2] = 0;
                break;
            case NoDirectionNoWeight:
                if (matrix[v1][v2] != 0)
                    edgeSize--;
                matrix[v1][v2] = 0;
                matrix[v2][v1] = 0;
                break;
            case DirectionWeight:
                if (matrix[v1][v2] != INF)
                    edgeSize--;
                matrix[v1][v2] = INF;
                break;
            case NoDirectionWeight:
                if (matrix[v1][v2] != INF)
                    edgeSize--;
                matrix[v1][v2] = INF;
                matrix[v2][v1] = INF;
                break;
        }
        return true;
    }

（3）getDegree系列方法

    int getDegree(int v);
    int getInDegree(int v);
    int getOutDegree(int v);

分别为获取v节点的度、入度、出度的方法。

第一个方法有一个统一的实现

public int getDegree(int v) {
        if (type == GraphType.NoDirectionWeight || type == GraphType.NoDirectionNoWeight)
            return getOutDegree(v); // 因为算起来比GetInDegree快
        else
            return getInDegree(v) + getOutDegree(v);
    }

邻接表实现

邻接表没有什么难度，也无需分类，直接遍历

@Override
    public int getInDegree(int v) {
        int count = 0;
        for (int i = 1; i < maxVertex+1; i++) {
            if(i==v)
                continue;
            Iterator<VertexNode> iterator = vexList[i].listIterator(0);
            while (iterator.hasNext()){
                if(iterator.next().vertex==v){
                    count++;
                    break;
                }
            }
        }
        return count;
    }

    @Override
    public int getOutDegree(int v) {
        return vexList[v].size();
    }

邻接矩阵实现

公式如上，只需要遍历邻接矩阵即可。

 @Override
    public int getInDegree(int v) {
        int degree = 0;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[i][v] != INF)
                        degree++;
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[i][v] != 0)
                        degree++;
                }
                break;
        }
        return degree;
    }

    @Override
    public int getOutDegree(int v) {
        int degree = 0;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[v][i] != INF)
                        degree++;
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[v][i] != 0)
                        degree++;
                }
                break;
        }
        return degree;
    }

（4）getNeighbor系列方法

    int getFirstNeighbor(int v); // none return -1
    int getNextNeighbor(int v,int v2); // none return -1

这两个方法是用来实现后面的算法的，实现起来也很简单

邻接表实现

  @Override
    public int getFirstNeighbor(int v) {
        if(vexList[v].size()!=0){
            return vexList[v].getFirst().vertex;
        }else
            return -1;
    }

    @Override
    public int getNextNeighbor(int v, int v2) {
        Iterator<VertexNode> iterator = vexList[v].listIterator();
        while (iterator.hasNext()){
            if(iterator.next().vertex==v2)
                if(iterator.hasNext())
                    return iterator.next().vertex;
                else
                    return -1;
        }
        return -1;
    }

邻接矩阵实现

   @Override
    public int getFirstNeighbor(int v) {
        if (type == GraphType.NoDirectionNoWeight || type == GraphType.DirectionNoWeight) {
            for (int i = 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != 0 && i != v) {
                    return i;
                }
            }
        } else {
            for (int i = 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != INF && i != v) {
                    return i;
                }
            }
        }
        return -1;
    }

    @Override
    public int getNextNeighbor(int v, int v2) {
        if (type == GraphType.NoDirectionNoWeight || type == GraphType.DirectionNoWeight) {
            for (int i = v2 + 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != 0 && i != v) {
                    return i;
                }
            }
        } else {
            for (int i = v2 + 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != INF && i != v) {
                    return i;
                }
            }
        }
        return -1;
    }

（5）getWeight方法

这个方法主要是用来作为后续算法的接口，为了把图类做封装。

一般来讲只有有权图的时候才会用到这个方法，定义如果不存在边的话返回INF。

邻接表实现

    @Override
    public int getWeight(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return INF;
        }
        Iterator<VertexNode> iterator = vexList[v1].listIterator();
        while (iterator.hasNext()) {
            VertexNode node = iterator.next();
            if (node.vertex == v2)
                return node.weight;
        }
        return INF;
    }

邻接矩阵实现

    @Override
    public int getWeight(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return INF;
        }
        return matrix[v1][v2];
    }

（6）深度优先搜索（DFS）

• 思想:

  从图中某个顶点V0出发，访问它，然后选择一个V0邻接到的未被访问的一个邻接点V1出发深度优先遍历图，当遇到一个所有邻接于它的结点都被访问过了的结点U时，回退到前一次刚被访问过的拥有未被访问的邻接点W，再从W出发深度遍历......直到连通图中的所有顶点都被访问过为止。

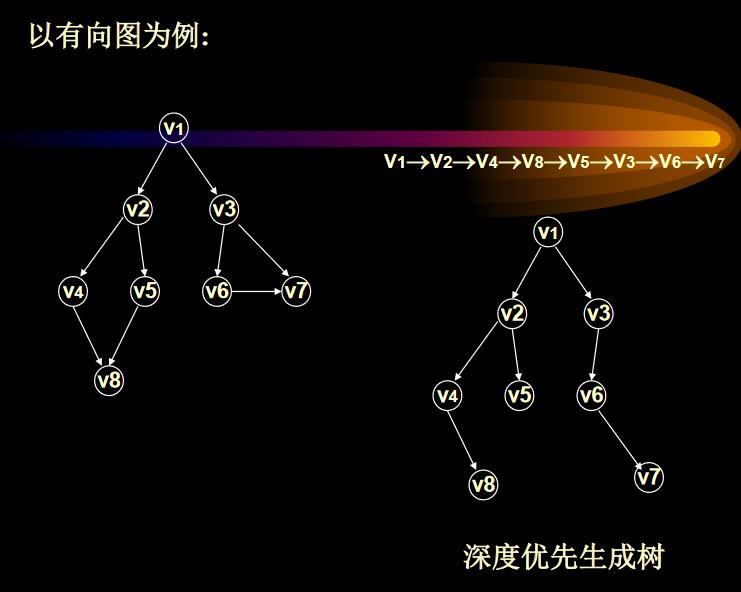
实现过程需要new一个boolean数组，标记节点是否访问过

邻接表和邻接矩阵的实现方式一致

@Override
    public String depthFirstSearch(int v) {
        boolean[] visited = new boolean[maxVertex + 1];
        StringBuffer rs = new StringBuffer();
        rs.append(v + " → ");
        DFS(v, visited, rs);
        return rs.toString();
    }

    private void DFS(int v, boolean[] visited, StringBuffer rs) {
        visited[v] = true;
        int next = getFirstNeighbor(v);
        while (next != -1) {
            if (!visited[next]) {
                rs.append(next + " → ");
                DFS(next, visited, rs);
            }
            next = getNextNeighbor(v, next);
        }
    }

（7）广度优先搜索（BFS）

• 思想

  从图中某顶点V0出发，在访问了V0之后依次访问v0的各个未曾访问过的邻接点，然后分别从这些邻接点出发广度优先遍历图，直至图中所有顶点都被访问到为止

  

  实现过程需要new一个boolean数组，标记节点是否访问过

  使用到了队列结构

  邻接表和邻接矩阵的实现方式一致

   @Override
      public String breathFirstSearch(int v) {
          StringBuffer rs = new StringBuffer();
          boolean[] visited = new boolean[maxVertex+1];
          rs.append(v + " → ");
          visited[v]=true;
          Queue<Integer> queue = new LinkedList<>();
          queue.offer(v);
          while (!queue.isEmpty()){
              v = queue.poll();
              int next = getFirstNeighbor(v);
              while (next!=-1) {
                  if (!visited[next]) {
                      rs.append(next + " → ");
                      visited[next] = true;
                      queue.offer(next);
                  }
                  next = getNextNeighbor(v,next);
              }
          }
          return rs.toString();
      }
  

完整代码

LinkGraph

import java.util.Iterator;
import java.util.LinkedList;
import java.util.Queue;

public class LinkGraph implements Graph {


    private LinkedList<VertexNode>[] vexList;
    private int edgeSize;
    private GraphType type;
    private int maxVertex;
    private static final int INF = 999999; // 用于有权图的无边表示
    Iterator<VertexNode> temp; // 用于缓存getNeighbor方法的Iterator

    public LinkGraph(GraphType type, int size) {
        vexList = new LinkedList[size + 1];
        for (int i = 1; i < size + 1; i++) {
            vexList[i] = new LinkedList();
        }
        maxVertex = size;
        edgeSize = 0;
        this.type = type;
    }

    @Override
    public boolean insertEdge(int v1, int v2, int weight) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        boolean contain = false;
        switch (type) {
            case DirectionNoWeight:
                weight = 1;
            case DirectionWeight:
                for (VertexNode vex : vexList[v1]) {
                    if (vex.vertex == v2)
                        contain = true;
                }
                if (!contain)
                    edgeSize++;
                vexList[v1].add(new VertexNode(v2, weight));
                break;
            case NoDirectionNoWeight:
                weight = 1;
            case NoDirectionWeight:
                for (VertexNode vex : vexList[v1]) {
                    if (vex.vertex == v2)
                        contain = true;
                }
                if (!contain)
                    edgeSize++;
                vexList[v1].add(new VertexNode(v2, weight));
                vexList[v2].add(new VertexNode(v1, weight));
                break;
        }
        return true;
    }


    @Override
    public boolean deleteEdge(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        Iterator<VertexNode> iterator;
        switch (type) {
            case DirectionNoWeight:
            case DirectionWeight:
                iterator = vexList[v1].listIterator(0);
                while (iterator.hasNext()) {
                    if (iterator.next().vertex == v2) {
                        iterator.remove();
                        edgeSize--;
                        break;
                    }
                }
                break;
            case NoDirectionWeight:
            case NoDirectionNoWeight:
                iterator = vexList[v1].listIterator(0);
                while (iterator.hasNext()) {
                    if (iterator.next().vertex == v2) {
                        iterator.remove();
                        edgeSize--;
                        iterator = vexList[v2].listIterator(0);
                        while (iterator.hasNext()) {
                            if (iterator.next().vertex == v1) {
                                iterator.remove();
                                edgeSize--;
                                break;
                            }
                            break;
                        }
                    }
                    break;
                }
        }
        return true;
    }

    @Override
    public int getDegree(int v) {
        if (type == GraphType.NoDirectionWeight || type == GraphType.NoDirectionNoWeight)
            return getOutDegree(v); // 因为算起来比GetInDegree快
        else
            return getInDegree(v) + getOutDegree(v);
    }

    @Override
    public int getInDegree(int v) {
        int count = 0;
        for (int i = 1; i < maxVertex+1; i++) {
            if(i==v)
                continue;
            Iterator<VertexNode> iterator = vexList[i].listIterator(0);
            while (iterator.hasNext()){
                if(iterator.next().vertex==v){
                    count++;
                    break;
                }
            }
        }
        return count;
    }

    @Override
    public int getOutDegree(int v) {
        return vexList[v].size();
    }

    @Override
    public String depthFirstSearch(int v) {
        boolean[] visited = new boolean[maxVertex + 1];
        StringBuffer rs = new StringBuffer();
        rs.append(v + " → ");
        DFS(v, visited, rs);
        return rs.toString();
    }

    private void DFS(int v, boolean[] visited, StringBuffer rs) {
        visited[v] = true;
        int next = getFirstNeighbor(v);
        while (next != -1) {
            if (!visited[next]) {
                rs.append(next + " → ");
                DFS(next, visited, rs);
            }
            next = getNextNeighbor(v, next);
        }
    }

    @Override
    public String breathFirstSearch(int v) {
        StringBuffer rs = new StringBuffer();
        boolean[] visited = new boolean[maxVertex+1];
        rs.append(v + " → ");
        visited[v]=true;
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(v);
        while (!queue.isEmpty()){
            v = queue.poll();
            int next = getFirstNeighbor(v);
            while (next!=-1) {
                if (!visited[next]) {
                    rs.append(next + " → ");
                    visited[next] = true;
                    queue.offer(next);
                }
                next = getNextNeighbor(v,next);
            }
        }
        return rs.toString();
    }

    @Override
    public GraphType getGraphType() {
        return type;
    }

    @Override
    public int getFirstNeighbor(int v) {
        if(vexList[v].size()!=0){
            return vexList[v].getFirst().vertex;
        }else
            return -1;
    }

    @Override
    public int getNextNeighbor(int v, int v2) {
        Iterator<VertexNode> iterator = vexList[v].listIterator();
        while (iterator.hasNext()){
            if(iterator.next().vertex==v2)
                if(iterator.hasNext())
                    return iterator.next().vertex;
                else
                    return -1;
        }
        return -1;
    } 
    
    @Override
    public int getSize() {
        return maxVertex;
    }

    @Override
    public int getWeight(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return INF;
        }
        Iterator<VertexNode> iterator = vexList[v1].listIterator();
        while (iterator.hasNext()) {
            VertexNode node = iterator.next();
            if (node.vertex == v2)
                return node.weight;
        }
        return INF;
    }

    private class VertexNode {
        int vertex;
        int weight;

        VertexNode(int vex, int weight) {
            vertex = vex;
            this.weight = weight;
        }

        VertexNode(int vex) {
            vertex = vex;
            this.weight = 1;
        }
    }
    
    @Override
    public int getEdgeSize() {
        return edgeSize;
    }
}

MatrixGraph

import java.util.LinkedList;
import java.util.Queue;

public class MatrixGraph implements Graph {

    public static void main(String[] args) {
        Graph graph = new MatrixGraph(GraphType.DirectionWeight, 10);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(4, 3, 1);
        graph.insertEdge(3, 8, 1);
        graph.insertEdge(6, 3, 1);
        graph.insertEdge(8, 9, 1);
        System.out.println(graph.getInDegree(7));
        System.out.println(graph.getOutDegree(3));
        System.out.println(graph.getDegree(3));
    }

    private int[][] matrix;
    private int edgeSize;
    private GraphType type;
    private int maxVertex;
    private static final int INF = 999999; // 用于有权图的无边表示

    public MatrixGraph(GraphType type, int size) {
        matrix = new int[size + 1][size + 1];
        maxVertex = size;
        edgeSize = 0;
        this.type = type;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 0; i < size + 1; i++) {
                    for (int j = 0; j < size + 1; j++) {
                        matrix[i][j] = INF;
                    }
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 0; i < size + 1; i++) {
                    for (int j = 0; j < size + 1; j++) {
                        matrix[i][j] = 0;
                    }
                }
                break;
        }
    }

      @Override
    public boolean insertEdge(int v1, int v2, int weight) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        switch (type) {
            case DirectionNoWeight:
                if (matrix[v1][v2] == 0)
                    edgeSize++;
                matrix[v1][v2] = 1;
                break;
            case NoDirectionNoWeight:
                if (matrix[v1][v2] == 0)
                    edgeSize++;
                matrix[v1][v2] = 1;
                matrix[v2][v1] = 1;
                break;
            case DirectionWeight:
                if (matrix[v1][v2] == INF)
                    edgeSize++;
                matrix[v1][v2] = weight;
                break;
            case NoDirectionWeight:
                if (matrix[v1][v2] == INF)
                    edgeSize++;
                matrix[v1][v2] = weight;
                matrix[v2][v1] = weight;
                break;
        }
        return true;
    }

    @Override
    public boolean deleteEdge(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return false;
        }
        switch (type) {
            case DirectionNoWeight:
                if (matrix[v1][v2] != 0)
                    edgeSize--;
                matrix[v1][v2] = 0;
                break;
            case NoDirectionNoWeight:
                if (matrix[v1][v2] != 0)
                    edgeSize--;
                matrix[v1][v2] = 0;
                matrix[v2][v1] = 0;
                break;
            case DirectionWeight:
                if (matrix[v1][v2] != INF)
                    edgeSize--;
                matrix[v1][v2] = INF;
                break;
            case NoDirectionWeight:
                if (matrix[v1][v2] != INF)
                    edgeSize--;
                matrix[v1][v2] = INF;
                matrix[v2][v1] = INF;
                break;
        }
        return true;
    }


    @Override
    public int getDegree(int v1) {
        if (type == GraphType.NoDirectionWeight || type == GraphType.NoDirectionNoWeight)
            return getInDegree(v1);
        else
            return getInDegree(v1) + getOutDegree(v1);
    }

    @Override
    public int getInDegree(int v) {
        int degree = 0;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[i][v] != INF)
                        degree++;
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[i][v] != 0)
                        degree++;
                }
                break;
        }
        return degree;
    }

    @Override
    public int getOutDegree(int v) {
        int degree = 0;
        switch (type) {
            case DirectionWeight:
            case NoDirectionWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[v][i] != INF)
                        degree++;
                }
                break;
            case DirectionNoWeight:
            case NoDirectionNoWeight:
                for (int i = 1; i < maxVertex + 1; i++) {
                    if (matrix[v][i] != 0)
                        degree++;
                }
                break;
        }
        return degree;
    }

    @Override
    public String depthFirstSearch(int v) {
        boolean[] visited = new boolean[maxVertex + 1];
        StringBuffer rs = new StringBuffer();
        rs.append(v + " → ");
        DFS(v, visited, rs);
        return rs.toString();
    }

    private void DFS(int v, boolean[] visited, StringBuffer rs) {
        visited[v] = true;
        int next = getFirstNeighbor(v);
        while (next != -1) {
            if (!visited[next]) {
                rs.append(next + " → ");
                DFS(next, visited, rs);
            }
            next = getNextNeighbor(v, next);
        }
    }

    @Override
    public String breathFirstSearch(int v) {
        StringBuffer rs = new StringBuffer();
        boolean[] visited = new boolean[maxVertex+1];
        rs.append(v + " → ");
        visited[v]=true;
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(v);
        while (!queue.isEmpty()){
            v = queue.poll();
            int next = getFirstNeighbor(v);
            while (next!=-1) {
                if (!visited[next]) {
                    rs.append(next + " → ");
                    visited[next] = true;
                    queue.offer(next);
                }
                next = getNextNeighbor(v,next);
            }
        }
        return rs.toString();
    }

    @Override
    public GraphType getGraphType() {
        return type;
    }

    @Override
    public int getFirstNeighbor(int v) {
        if (type == GraphType.NoDirectionNoWeight || type == GraphType.DirectionNoWeight) {
            for (int i = 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != 0 && i != v) {
                    return i;
                }
            }
        } else {
            for (int i = 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != INF && i != v) {
                    return i;
                }
            }
        }
        return -1;
    }

    @Override
    public int getNextNeighbor(int v, int v2) {
        if (type == GraphType.NoDirectionNoWeight || type == GraphType.DirectionNoWeight) {
            for (int i = v2 + 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != 0 && i != v) {
                    return i;
                }
            }
        } else {
            for (int i = v2 + 1; i < maxVertex + 1; i++) {
                if (matrix[v][i] != INF && i != v) {
                    return i;
                }
            }
        }
        return -1;
    }
    
    @Override
    public int getSize() {
        return maxVertex;
    }

    @Override
    public int getWeight(int v1, int v2) {
        if (v1 < 1 || v1 > maxVertex || v2 < 1 || v2 > maxVertex) {
            System.out.println("无效输入，退出");
            return INF;
        }
        return matrix[v1][v2];
    }
    
    @Override
    public int getEdgeSize() {
        return edgeSize;
    }
}