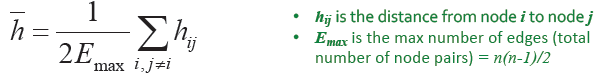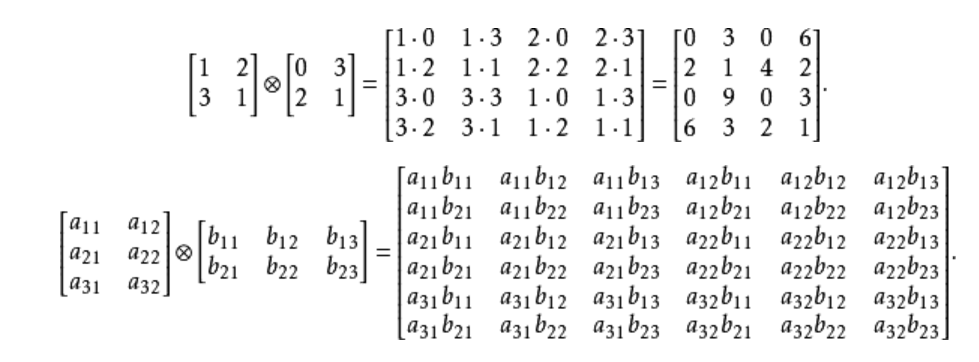本节重点:如何衡量一个网络 (网络量化)
网络的关键属性:
1. 度的分布:P(k)
2. 路径长度:h
3. 集聚系数(clustering coefficient):C
4. 连通分量(connected components):s
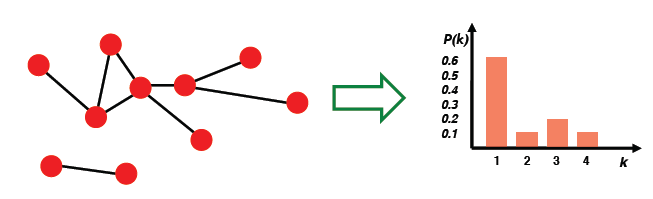
1. 度的分布 degree distribution:P(k)
统计每个节点的度,形成归一化后的直方图
2. 路径
3. 距离:最短路径
4. 直径:网络中任意节点最短距离的最大值
5. 平均路径长度(针对连通图或强连通的有向图)
6. 集聚系数(无向图):
首先,看单个节点,其与邻居的连接关系如何。例如节点i,他的度为ki,ei是节点i的邻居间的边的数量
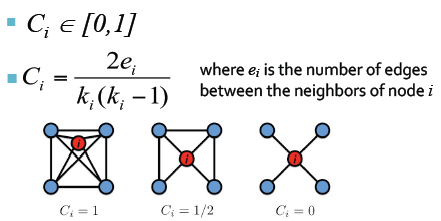
平均集聚系数:

7. 连通性: 最大连通分量(子图/分支)的尺寸,使用BFS广度优先方式
接下来开始量化现实世界中的网络
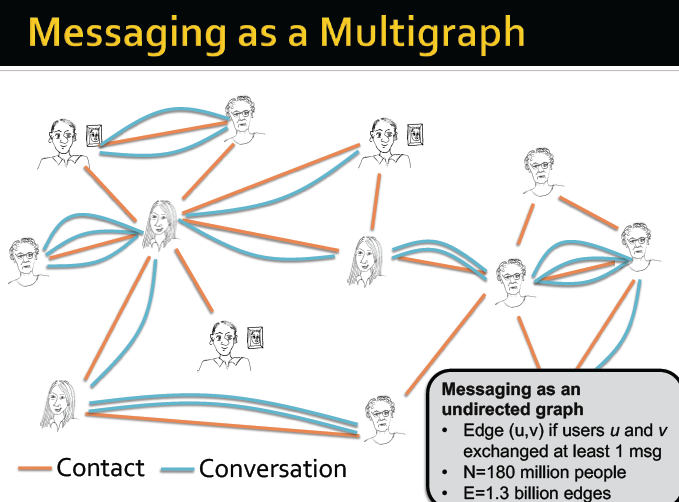
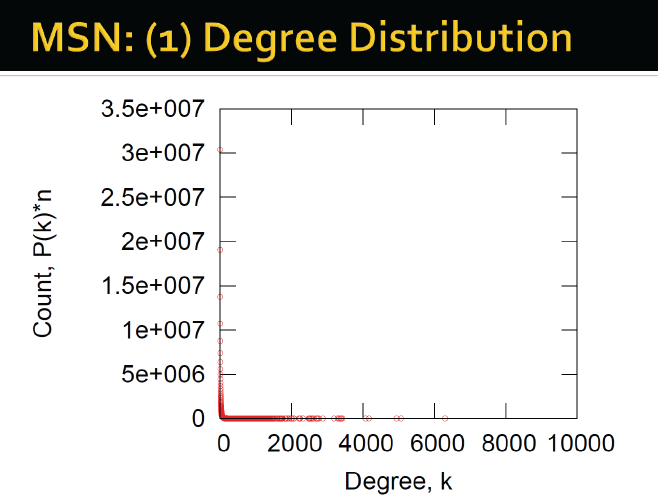
MSN的联系网络
对分布取log
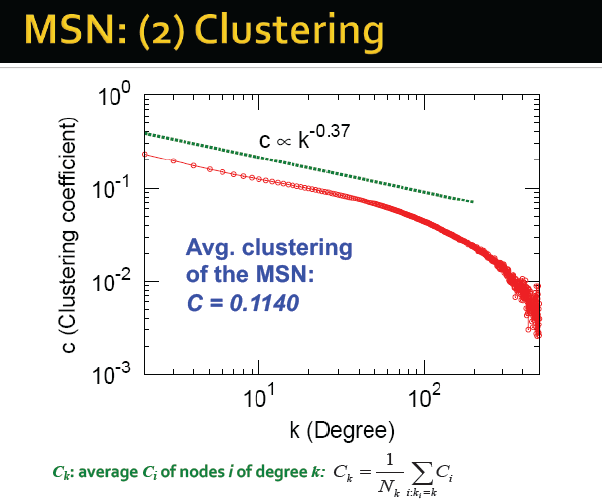
集聚:
度对应的集聚系数
弱连通分支尺寸的统计:
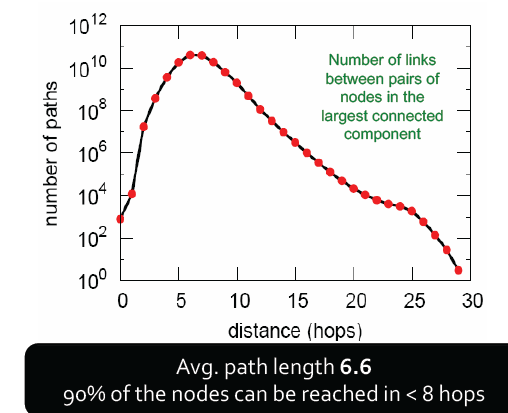
若连同分支的半径:
平均路径长度为6.6,90%的节点可最小经由8跳后连接
随机图模型 Erdös-Renyi Random Graphs
两类变量(针对无向图):
Gnp:n个节点,边的出现(顶点相连)满足概率p
Gnm:n个节点,均匀随机选取m个边

n和p不能唯一确定一个图谱,该图谱是随机过程的结果
Gnp的属性:
度的分布:p(k) —— 满足二项分布
路径长度:h
集聚系数: C
p(k)表示度为k的节点的概率
k- 表示度的期望
均值,和方差可通过公式计算
根据大数定律,随着网络规模的增大,分布变得越来越窄,因而可以确定一个点的度在k附近
随机模型的集聚系数较小
如果我们生产不同网络规模但平均度为k的网络,随着网络规模的增大,集聚系数以C的倍数衰减
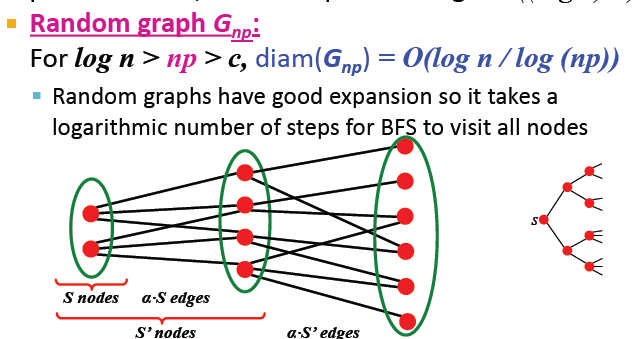
膨胀Expansion:
图G(V,E)的膨胀α:

事实上,对于一个节点数为n,expansion为α的图,对于所有节点的对,路径长度O((log n)/α).
随机图具有良好的可扩展性,因此BFS访问所有节点需要对数步长
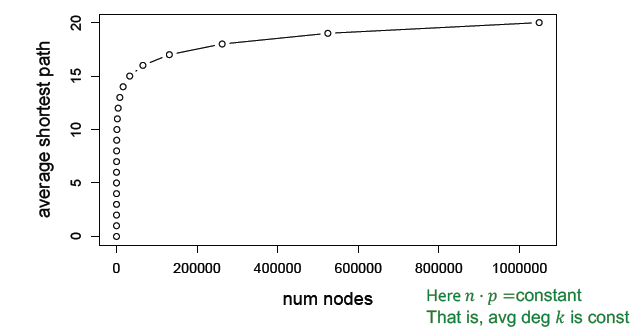
随机图的规模可以变得很大,但节点间的距离会保持在较小的数
对随机图的评估:
(
Giant Component
一个规模很大的网络中,可能存在多于一个的连通分支/连通分量(Connected Component),即网络中并非所有节点都连通。但是在真实网络中通常存在一个规模很大的连通分支(即Giant Component)会包含网络中大多数的节点(比如超过80%的节点)。
如果一个人刚注册人人,还没加好友,那他就是一个孤立点(没有和任何其他点相连)。而一旦有了好友,就不再是孤立点。如果某个学校规定学生在人人只能加本校好友,不能有外校好友,那么这个学校的学生也会构成一个小的独立的连通分支。不过可以想到,人人里绝大多数的同学都处在一个超大的连通分支中,真正孤立的节点或小的连通分支所占用户数是很少的。
Facebook的数据显示约99.7%的用户处在一个超大的Giant Component中。
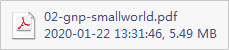
随机图的图结构随p变化的示意图:
当p==0时,该图各节点无连接
当p==1/(n-1),即平均度为1时,出现giant component
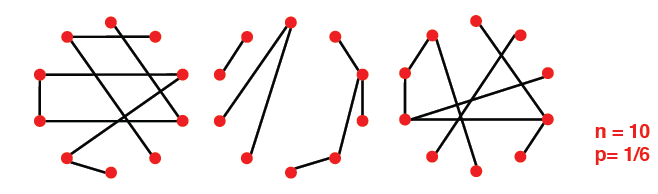
当p==c/(n-1)时,平均度为一常数,但有多数的孤立点
当p==log(n)/(n-1)时,更少的孤立点
当p==(2*log(n))/(n-1)时,没有孤立点
当p==1时,为完全连通图
giant component的出现:(这个没太看懂)
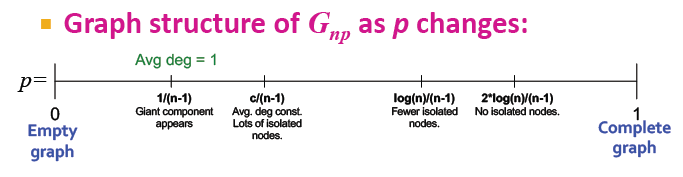
通过MSN验证上面的推论:
1. 度的分布:二项分布→不成立
2. 平均路径长度:O(log n) MSN中,n为180M,log n≈8.2 实际为6.6 →满足推论
3. 集聚系数: 度的期望/节点个数 约在8*10-8 不等于0.11→不满足推论
4. 最大连通分量:若度的平均期望>1,则giant component存在,实际上包含99%的点→满足推论
因此,在在很大程度上,现实世界的网络,并不是随机图
随机图存在的问题:
度的分布与现实世界的网络不同
在大多数真实的网络中,giant component并不是通过phase transition产生的
集聚系数太低
既然如此,我们为什么还有学习随机图模型?
因为:
他是其他类型模型的参考模型
帮助我们理解和计算许多属性,从而与真实数据做比对
它将帮助我们理解某一特性在多大程度上是某个随机过程的结果
因此:
虽然随机图模型不实际,但是很有用!
最小世界模型 the small world model
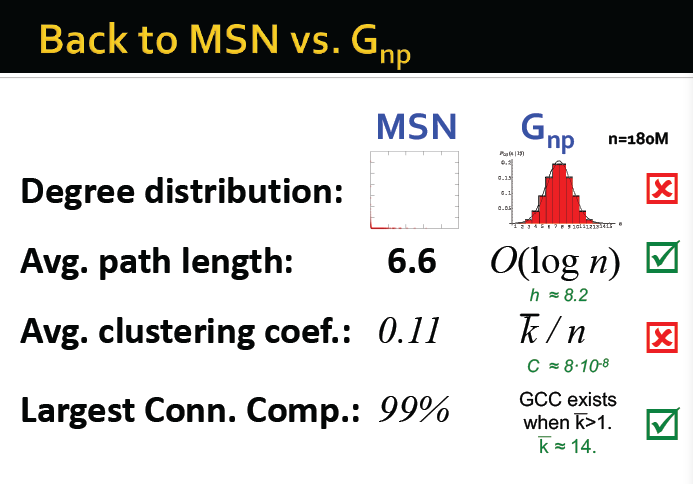
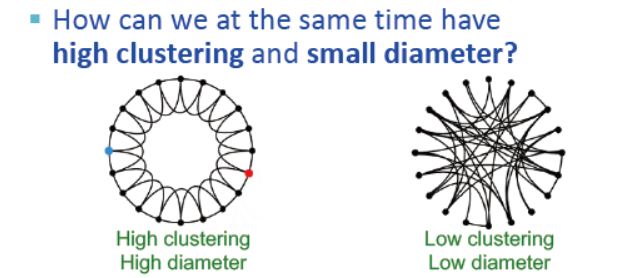
在具有高集聚的情况下同时路径最短?
在上面的推理中,MSN网络的集聚系数的量级比随机图的高7个量级
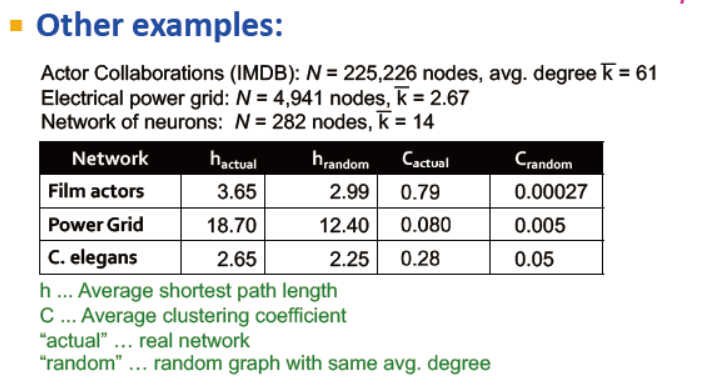
其他一些真实网络的例子,如:
演员合作网络,电网网络,神经元网络,他们的平均路径长度与随机网络的量级一致,但集聚稀疏的量级比随机网的大
最小世界:高集聚,半径的量级为log n
集聚意味着边缘的局部性
随机性使得捷径存在

最小世界模型的两个成分:
1. 从一个低维规则的晶体开始
在例子中,我们使用一个环作为晶体
拥有高的集聚系数
2. 连接:引入随机性 (捷径)
添加/删除边,用于生成连接较远的晶体间的捷径
对于每一条边,移动另一端点到随机端点的概率为p
下图中,横轴为移动概率p,左纵轴为集聚系数,右纵轴为平均路径长度,可以看出,p的概率越大,集聚系数下降,平均路径长度下降。从降低的斜率来看,需要较大的随机性来破坏集聚性,但较小的就能创造最短路径。
如何创造一个最小世界?—— 一些随机的连接
Watts Strogatz Model:
提供了集聚性与最小世界的相互作用
捕捉许多现实网络的结构
现实网络的高集聚性
没有引向正确的度分布???(不太确定)
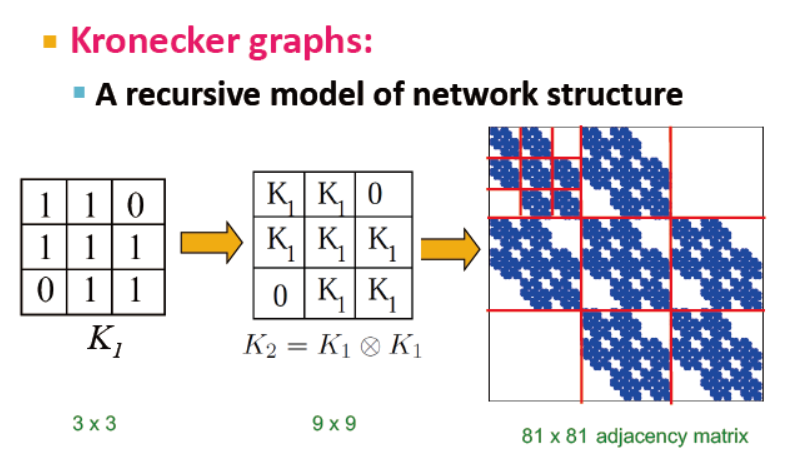
Kronecker Graph Model
创建大的真实图谱
设想:如果我们递归生成网络会怎么样?
递归生成网络的结构会是怎样的?→ 自相似性
对象类似于自身的一部分:整体与一个或多个部分形状相似
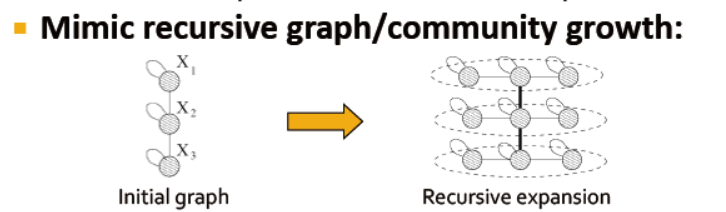
模拟递归的图谱生成/社区增长:
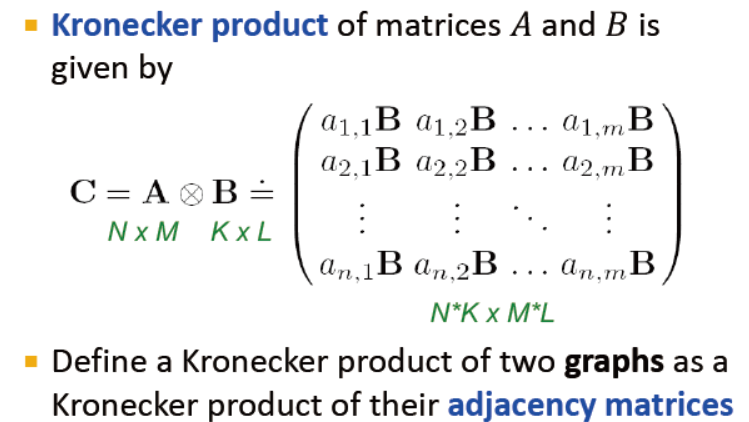
Kronecker product
克罗内克积:是生成自相似矩阵的方式
定义两个图的克罗内克积,主要是使用两图的连接矩阵
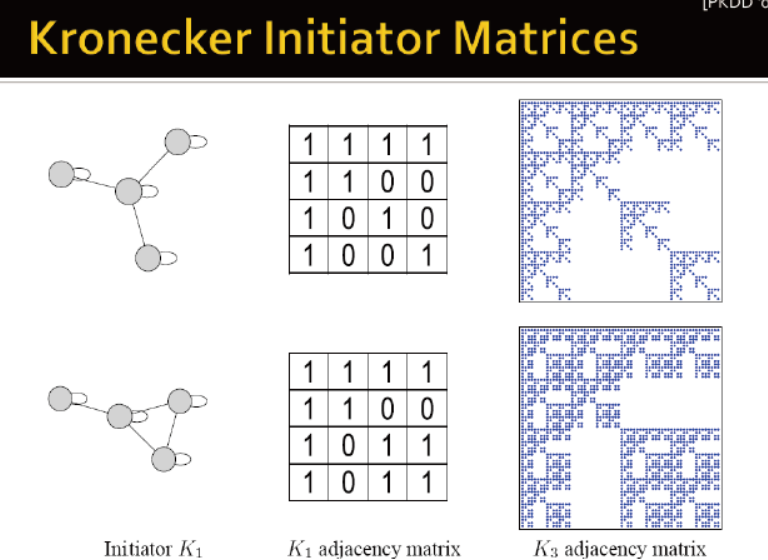
克罗内克图是通过图的克罗内克积的迭代生成的
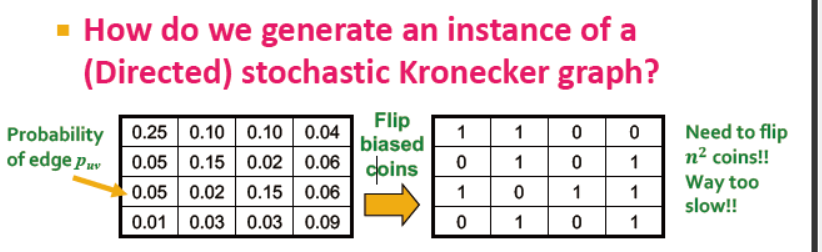
随机克罗内克图:
1. 生成n*n的概率矩阵
2. 计算概率矩阵的克罗内克积
3. 对于最后的结果,每个元素表示两个端点间的连接概率
得到概率矩阵后如何得到图? 抛硬币? 那这样需要抛n²次的硬币,太慢
是否有更快的方式?
是的
设想:探索克罗内克图的递归结构
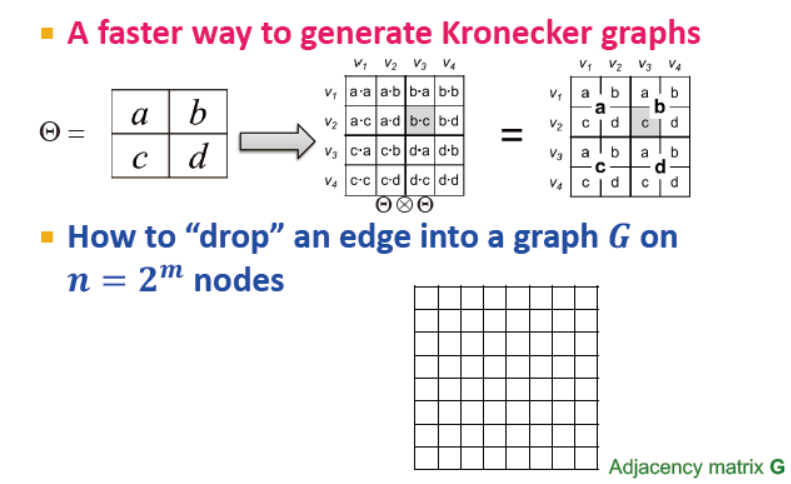
逐个将图的边放置?那么如何放置一个具备n=2^m个端点的图的边?→ 拆解并重插入
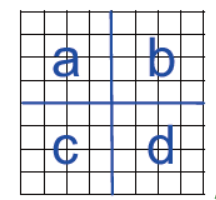

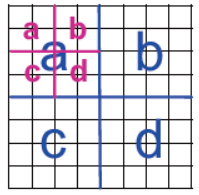
快速生成克罗内克图的算法:(理解得不是很透)
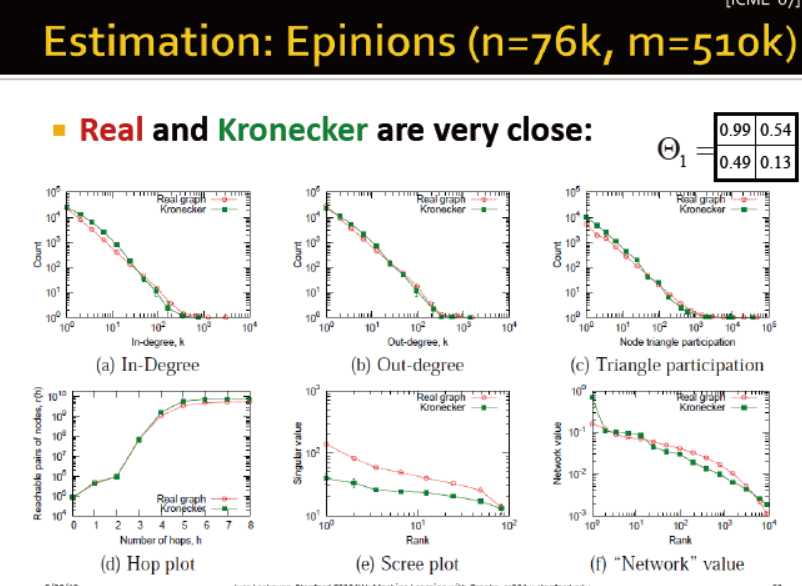
真实网络与克罗内克较为相似