选择排序算法——简单选择排序、堆排序排序 | 数据结构

选择排序

算法思想：每一趟在待排序元素中选取关键字最小或者最大的元素加入到有序子序列中。

简单选择排序

即选择排序最直接的实现方式。

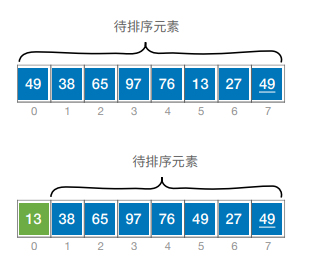
在这里中每次选择待排序序列中最小的那个元素，然后与已经有序的子序列的下一位交换位置。待排序序列缩短，循环往复，直到待排序序列还剩一个元素时终止。

void swap(int &a, int &b) {
	int temp = a;
	a = b;
	b = temp;
}

//简单选择排序
void SelectSort(int A[], int n) {
	int minpos;
	for (int i = 0; i < n-1; i++) {		//一共进行n-1趟，最后一个元素不用再进行
		minpos = i;						//假设当前元素是最小的，记录其下标
		for (int j = i; j < n; j++) {
			if (A[minpos] > A[j]) {		//若找到了更小的元素，更新下标
				minpos = j;
			}
		}
		if(minpos != i) swap(A[i], A[minpos]);	//交换位置
	}
}

算法分析

• 空间复杂度：O(1)，需要常量个辅助空间。

• 时间复杂度：该算法与序列内部状态无关，无论有序、乱序或者逆序排列都是O(n^2)

  • 其比较次数是固定的$$(n-1)+(n-2)+…+1 = frac{n(n-1)}{2}$$

• 简单选择排序算法是不稳定的算法。eg：3 3 1，第一次排序之后两个3的相对次序发生了变化。

• 算法评价：简单、容易实现，适用于待排序序列比较小的情况。

• 算法适用：可用于顺序表、链表这样的数据结构。(链表也是可以的。具体实现就是记录位置然后交换元素的内容即可)

---

堆排序

算法思想：堆排序是堆简单选择排序的改进，利用每趟比较后的结果，也就是在找出关键字值最小记录的同时，也找出关键字值较小的记录，则可减少后面的选择中所用的比较次数，从而提高整个排序过程的效率。

堆的定义

把具有如下性质的数组A[1……n]表示的完全二叉树称为最大堆，也称大根堆、大顶堆：A[i] >= A[2i]并且A[i]>=A[2i+1]。(即父节点大于其两个孩子节点)。

把具有如下性质的数组A[1……n]表示的完全二叉树称为最小堆，也称小根堆、小顶堆：A[i] <= A[2i]并且A[i]<=A[2i+1]。

注意：

• 二叉树的顺序存储来表示完全二叉树时，所用数组需要从1开始！
• i的左孩子为2*i，i的右孩子为2*i+1，i的父节点为i/2向下取整，若i>n/2向下取整时，当前节点为叶子节点，否则为分支节点。

如图所示：数组是其存储结构，下面的二叉树是其逻辑视图，表示一个大根堆。

建立一个大根堆

一个大根堆的基本要求就是每个逻辑上的父节点都大于其孩子节点，所以基本思路就是检查每一个非终端节点，看其是否满足大根堆的要求，不满足时进行调整。

从最后一个非终端节点开始往前检查，若不满足大根堆的要求时，将当前节点与其更大的一个孩子进行交换。当然调整过程中会发生下一层的子树不再满足的情况，则对下一层的子树也进行相应的调整。

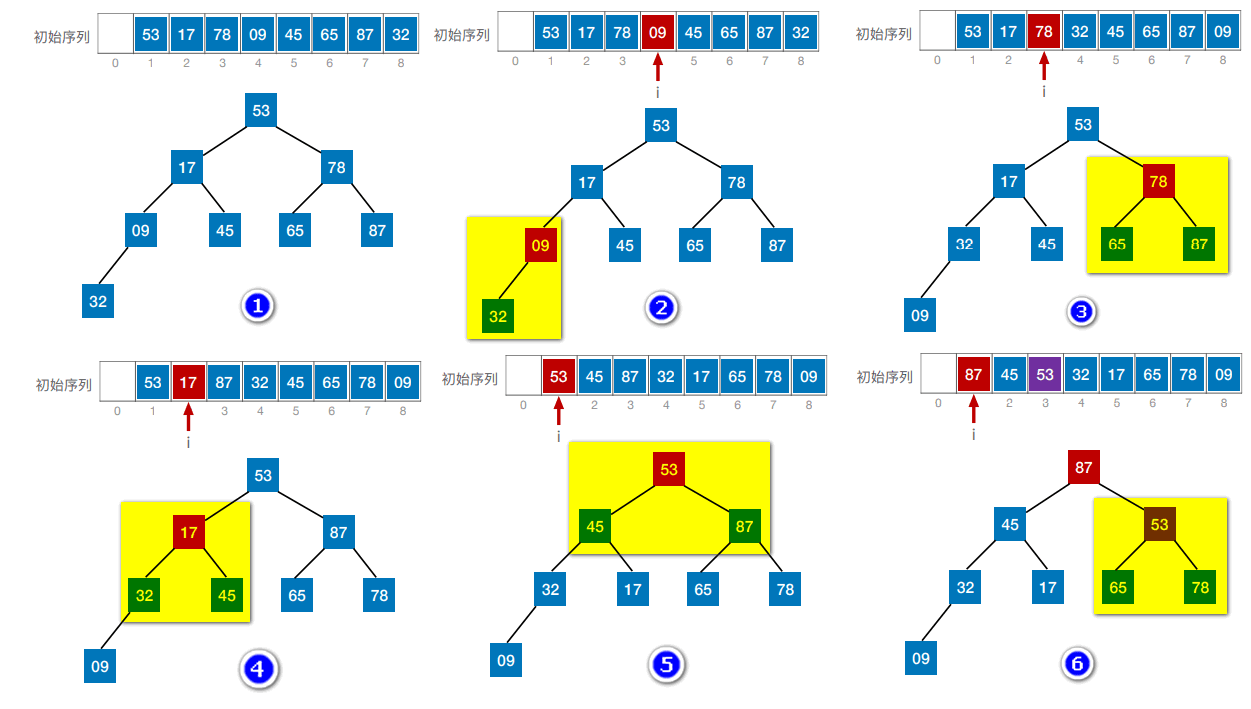
当第五步调整完之后，根节点的右子树不再满足大根堆的要求，所以还需要再对其进行额外的调整。

最终调整结果如图所示：

//大根堆调整
void MaxHeapAdjust(int A[], int k, int len) {
	A[0] = A[k];	//暂存待调整子树的根节点
	for (int i = 2 * k; i <= len; i *= 2) {	//沿着值较大的子节点向下筛选
		if (i+1 <= len && A[i] < A[i + 1])		//选择较大的孩子节点
			i++;
		if (A[0] >= A[i]) break;	//若原本就符合大根堆的要求，则结束
		else {
			A[k] = A[i];	//不符合时就进行替换
			k = i;			//修改k值，以便于继续向下调整当前堆的子树
		}
	}
	A[k] = A[0];			//填入最终位置
}

//建立大根堆
void BuildMaxHeap(int A[],int len) {
	for (int i = len/2; i >= 1; i--)	//从最后一个非终端节点向前进行调整
		MaxHeapAdjust(A, i, len);
}

这段代码来自王道，不得不说代码写的非常精炼。选择两个孩子中较大的那段代码，非常巧妙的包含了所有情况，i+1<=len，就包含了当前节点只有一个孩子的情况，此时k=4,i=8,len=8,不会执行后续的语句，从而避免了A[i+1]导致数组越界的情况。而若A[i]<A[i+1]时，i++条件满足时i会指向值大的那个孩子节点。

堆排序

基本思想：将当前堆顶的元素与当前最大的叶子节点交换位置，然后将剩下的n-1个元素再次整理成为堆，重复执行上述过程，最后直到生意一个元素时停止。这是整个序列就是一个从小到大排序的序列。

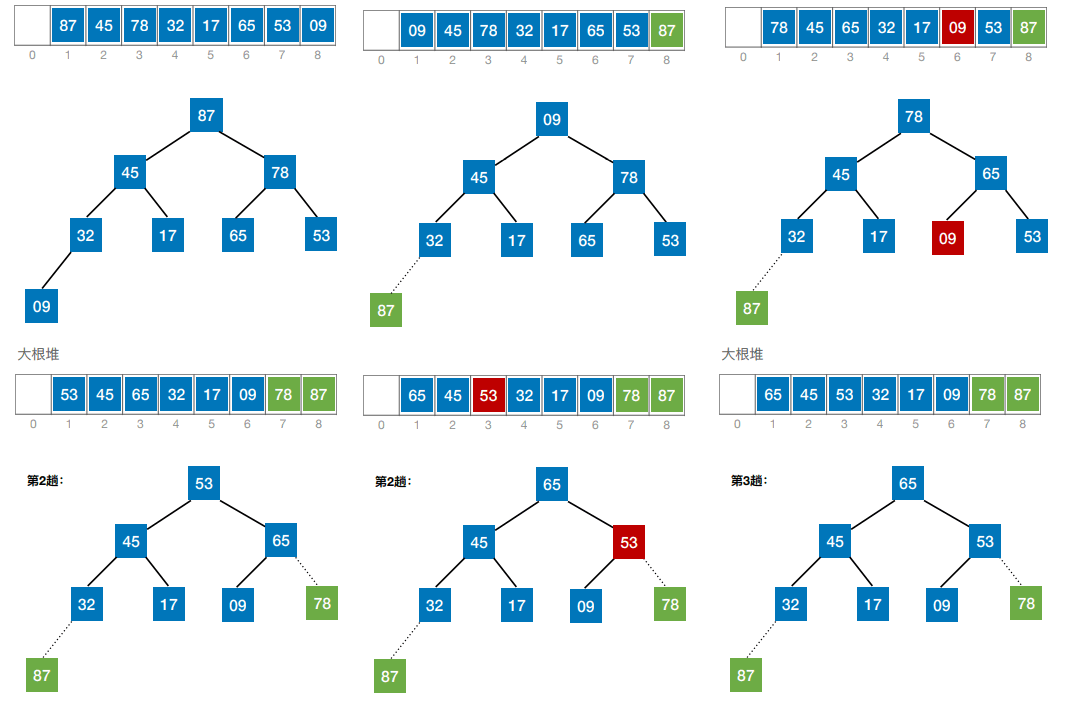
步骤如上如所示：整理成堆 —— 堆顶元素与堆底元素交换位置 —— 调整新的堆 —— 重复执行。

最终执行结果：

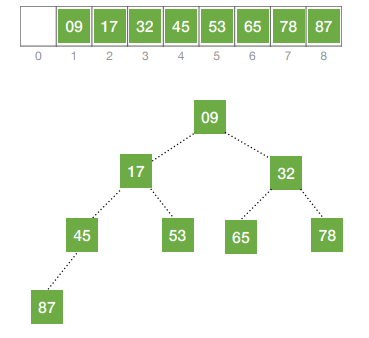
void swap(int &a, int &b) {
	int temp = a;
	a = b;
	b = temp;
}

//大顶堆排序
void MaxHeapSort(int A[], int n) {
	BuildMaxHeap(A, n);
	for (int i = 1; i <= n - 1; i++) {	//一共进行n-1趟排序
		//先调整成堆
		MaxHeadAdjust(A,1,n-i+1);
		//交换位置
		swap(A[1], A[n-i+1]);	//堆顶元素和最后一个元素交换
	}
}

算法分析

• 空间复杂度：O(1)，显然只需要常量个辅助空间。

• 时间复杂度：O(n*log2_n)

参考大根堆调整的代码，一个节点向下调整一层，最多需要对比2次，一个具有N个节点的数组，逻辑上树高为h，（$$h = lfloor log_2{n} floor + 1$$），若当前节点在第i层，则这个节点最多需要调整h-i层，从而关键字的对比次数不超过2(h-i)次。

第i层最多有$$2^{i-1}$$个节点，且只有第1层到第h-1层的节点才需要调整。

则将整个树调整成为大根堆，关键字的对比次数不超过4n，从而建立堆的时间复杂度为O(n)。

而在实际代码中，每次调整堆都是从根节点向下调整，也就是说根节点至多调整h-1次，而每调整一次最多对比关键字2次，从而每一趟排序调整的时间复杂度不超过O(h) = O(log2_n)。一共会进行n-1趟，总的时间复杂度是O(n*log2_n).

• 堆排序算法是不稳定的算法，再大根堆调整的算法中，当两个孩子值相同时，优先与左孩子进行交换位置。eg：1 2 2，对其进行排序，调整成堆2 1 2，然后根节点与末尾节点互换位置，导致两个2的先后次序发生了变化。
• 算法适用：顺序表和单链表均可。

大根堆的链表代码实现

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;

//链表定义
typedef struct LinkNode{
	int data;
	struct LinkNode* next;
}LinkNode,*LinkList;

//获取当前链表的最后一个节点
LinkNode* LastNode(LinkList L, int len) {
	LinkNode *p = L->next;
	int index = 1;
	while (index < len) {
		index++;
		p = p->next;
	}
	return p;
}

//交换两个链表元素的值
void swap(LinkNode &a, LinkNode &b) {
	int temp = a.data;
	a.data = b.data;
	b.data = temp;
}

//大根堆调整
void MaxHeapAdjust(LinkList &L,int k,int len) {
	int i = k;

	while(i <= len/2){
		LinkNode* pre = L->next;
		LinkNode* parent = nullptr;
		LinkNode* lchild = nullptr;
		LinkNode* rchild = nullptr;

		int index = 1;
		while (index < i) {
			pre = pre->next;	//找到了当前的节点
			index++;
		}
		parent = pre;		//父节点的位置

		//寻找其左右孩子
		while (index < 2*i) {
			pre = pre->next;
			index++;
		}
		lchild = pre;		//一定有左孩子
		if (2*i+1 <= len) rchild = pre->next;//若存在右孩子

		if (rchild != nullptr && lchild->data < rchild->data) {
			if (parent->data < rchild->data) {
				swap(*parent, *rchild); //与右孩子交换
				i = 2*i+1;
			}
			else if (parent->data < lchild->data) {
				swap(*parent, *lchild);//与左孩子进行交换
				i = 2*i;
			}
			else break; //满足条件，结束循环
		}
		else if (parent->data < lchild->data) {
			swap(*parent, *lchild);//与左孩子进行交换
			i = 2*i;
		}
		else break;	//满足条件，结束循环
	}
}

//建立大根堆
void BuildMaxHeap(LinkList &L,int len) {
	for (int i = len/2; i >= 1; i--) {	//从逻辑上的最后一个非终端节点向前建立
		MaxHeapAdjust(L,i,len);
	}
}

//大根堆排序
void MaxHeapSort(LinkList &L,int len) {
	BuildMaxHeap(L, len);				//初始建堆
	for (int i = 0; i < len - 1; i++) { //len个元素，共进行len-1趟排序
		MaxHeapAdjust(L,1,len-i);		//调整大根堆
		//堆顶元素和最后一个元素交换位置
		swap(*(L->next), *(LastNode(L,len-i)));
	}
}

int main()
{
	LinkList L = (LinkNode*)malloc(sizeof(LinkNode));//头节点
	L->next = nullptr;
	LinkNode* pre = L;

	srand(time(0));
	for (int i = 0; i < 8; i++) {
		LinkNode* q = (LinkNode*)malloc(sizeof(LinkNode));
		int randnum = rand() % 100; //0 - 99之间的随机数
		q->data = randnum;
		q->next = nullptr;
		pre->next = q;
		pre = pre->next;
	}
	
	//输出链表的元素
	cout << "初始链表元素为：";
	pre = L->next;
	while (pre != nullptr) {
		cout << pre->data << " ";
		pre = pre->next;
	}
	cout << endl;

	//建立一个大根堆
	BuildMaxHeap(L, 8);
	//输出链表的元素
	cout << "初始大根堆元素为：";
	pre = L->next;
	while (pre != nullptr) {
		cout << pre->data << " ";
		pre = pre->next;
	}
	cout << endl;

	//输出链表的元素
	MaxHeapSort(L, 8);
	cout << "大根堆排序结果为：";
	pre = L->next;
	while (pre != nullptr) {
		cout << pre->data << " ";
		pre = pre->next;
	}
	cout << endl;
}

小根堆的实现

#include <iostream>
using namespace std;

void swap(int &a, int &b) {
	int temp = a;
	a = b;
	b = temp;
}

//小根堆的调整
void MinHeapAdjust(int A[], int k, int len) {
	A[0] = A[k];	//暂存
	for (int i = 2*k; i <= len; i *= 2) {
		if (i+1 <= len && A[i] > A[i+1])	//小根堆是选择孩子中较小的那个
			i++;
		if (A[0] <= A[i]) break;
		else {
			A[k] = A[i];
			k = i;
		}
	}
	A[k] = A[0];	//填入最终位置
}

//建立小根堆
void BuildMinHeap(int A[], int len) {
	for (int i = len/2; i >= 1; i--)	//从最后一个非终端节点向前调整
		MinHeapAdjust(A, i, len);
}

//小根堆排序
void MinHeapSort(int A[], int n) {
	BuildMinHeap(A, n);
	for (int i = 1; i <= n - 1; i++) {
		//先调整堆
		MinHeapAdjust(A,1,n-i+1);
		//堆顶和最后一个元素交换位置
		swap(A[1], A[n-i+1]);
	}
}

int main()
{
	int A[9] = { 0,53,17,78,9,45,65,87,32 };
	BuildMinHeap(A, 8);
	for (int i = 1; i <= 8; i++) {
		cout << A[i] << " ";
	}
	cout << endl;
	MinHeapSort(A, 8);
	for (int i = 1; i <= 8; i++) {
		cout << A[i] << " ";
	}
	return 0;
}

堆排序的应用1 —— 优先级队列

常见的操作是使用堆来实现优先级队列，这种优先级队列只对最高或者最低优先级的元素进行删除，但是在任何时刻，都可以把任意优先级的元素插入到优先级队列。

操作系统中的进程管理是优先级队列的一个应用实例，系统中使用一个优先队列来管理进程。 每个进程有进程任务号和优先级两部分组成。当有多个进程排队时，优先级高的先操作。

堆排序的应用2 —— 找前K个最大的数

例如给定了N个数，要在其中找到最大的K个数。

先取前K个数建立小根堆，然后从剩下的序列中顺序读取数据，比小根堆堆顶元素小的直接丢弃，比小根堆堆顶元素大的则进行替换它，之后重新调整成小根堆。这样最后读取完毕之后堆中的数据就是堆的前K个最大的值。