1 为什么随机梯度下降法能work?
https://www.zhihu.com/question/27012077中回答者李文哲的解释
2 随机梯度下降法的好处?
(1)加快训练速度(2)噪音可以使得跳出局部最优
3 权衡方差和偏差:
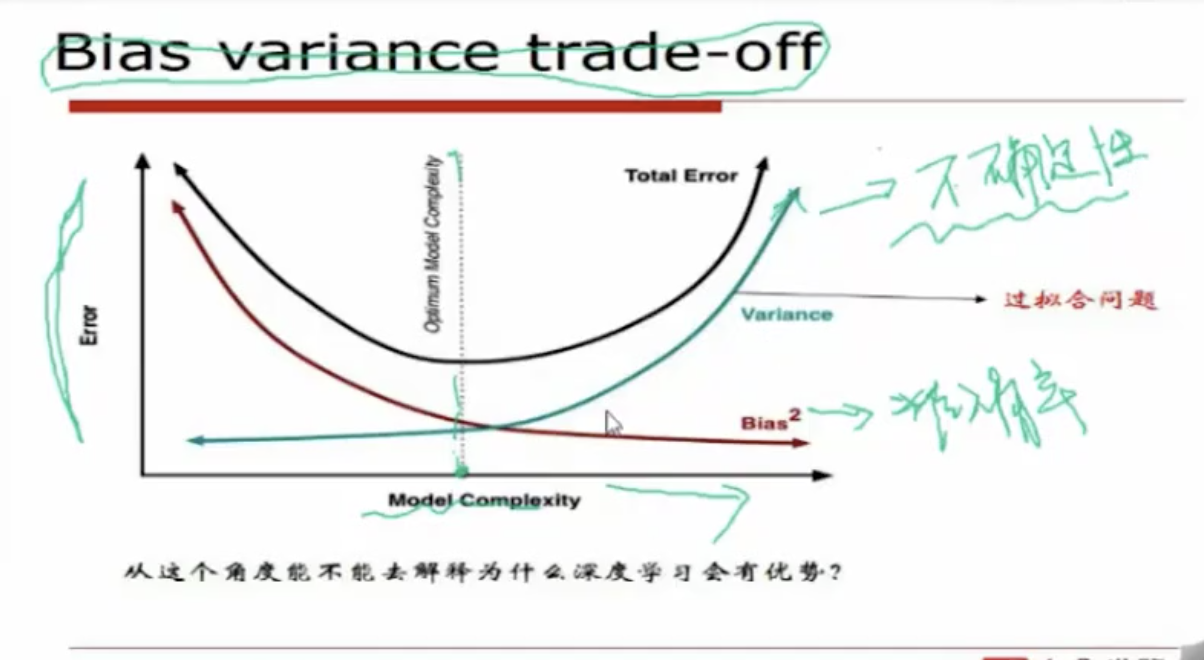
偏差反映的是模型的准确度(对训练数据的吻合程度),方差则反映模型的稳定性(对测试数据的泛化能力)。模型越复杂,偏差越小,方差越大。
4 减少过拟合的方法:
(1)减少特征个数
(2)增大数据量
(3)引入正则项
5 L1和L2正则
(1)
L0范数:||x||0为x向量各个非零元素的个数
L1范数: ||x||1 为x向量各个元素绝对值之和。
L2范数: ||x||2为x向量各个元素平方和的1/2次方,L2范数又称Euclidean范数或者Frobenius范数
(2)
L0正则的特点是:防止过拟合,并给出稀疏结果用于特征选择,但由于加L0后问题很难求解,所以一般用L1来做稀疏。
L1正则的特点是:防止过拟合,给出稀疏结果,常用于特征选择。
L2正则的特点是防止过拟合。
(3)
L0能得到稀释结果比较好理解,那么为什么L1也能得到稀疏结果呢?
首先,加了正则之后的优化问题可以如下等价:

然后来看看W是二维的情况下:

可以发现,L2所规定的约束范围与等高线的交点通常不在坐标轴上,而L1由于范围是一个棱形,等高线与其交点刚好落在坐标轴上,对应于w1为0。当W是一个更高维的情况也是类似,这就解释了为什么L1能给出一个稀疏的结果,而L2不能。
*(4)L2正则的梯度很好求解,但是L1则不能简单求导解决,往往是用下面三种方法来解决:

(5)L1正则有什么问题?
如果有几个变量相关性比较大,它会随机选出其 中之一, 而不考虑其他的变量。