顺序队列（循环队列）

概述

队列（queue）是一种只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出（First In First Out）的线性表，简称FIFO。

允许插入的一端称为队尾，允许删除的一端称为队头。

因为已经限制了插入和删除的位置，所以对于队列，插入和删除时只需要考虑满和空两种状态。

线性表存储结构分为顺序存储和链式存储，这里只讨论静态分配的顺序存储结构。

约定

为了方便起见，我们约定：

1、初始化建队列时，令队头指针m_nFront和队尾指针m_nRear等于0，即m_nFront = m_nRear = 0;

2、m_nFront指向队头元素的位置，m_nRear指向队尾元素的下一位。

关键点

1、顺序队列的假上溢现象

顺序队列的操作分别在队头和队尾两端进行。在出队时，队头m_nFront和队尾m_nRear的值都是只增加（向队列长度m_nCount）靠近；如果仅通过m_nRear == m_nCount来判断顺序队列是否满队，此时可能存在m_nRear已经指向m_nCount，同时m_nFront > 0（已有元素出队），顺序队列中实际的元素个数远小于m_nCount而不能做入队操作的情况，导致元素出队后的空闲存储空间永远无法重用，造成假上溢。如下图：

解决方法：

为克服假上溢，可将顺序队列想象为一个首尾相接的环状空间，称为循环队列。在循环队列中出队入队时，头尾指针仍向前移动进行加1操作，当头尾指针指向m_nCount时，头尾指针加1操作的结果重新指向下界0（加1后对m_nCount做取余数运算）。

2、判断队空和队满

想象成循环队列后，当入队时，m_nRear向前追赶m_nFront，出队时，m_nFront向前追赶m_nRear，故存在队空和队满时都有m_nFront == m_nRear的情况，因此无法通过m_nFront == m_nRear来判断队空还是队满。

解决方法：

牺牲存储空间中的一个存储单元，使队空和队满的判断条件不同即可，具体的：

1）出队时，m_nRear == m_nFront时，表示队空，此时不能出队。

2）入队时，当（m_nRear + 1） % m_nCount == m_nFront时，表示队满，此时不能入队。

代码实现

Queue.h

/*******************************************************
* File Name：Queue.h
* Description：队列类头文件，自主实现一个队列数据结构
* Version：V1.0 
* Author：Mengjia 
* Date：2018-06-02 
* Copyright (C)2018, Mengjia
* Others:自主实现一个队列数据结构
#pragma once
*******************************************************/
template<class T>
class CQueue
{
private:
    T * m_pData;        //数据指针
    int m_nCount;        //队列长度
    int m_nFront;        //当前队列头部
    int m_nRear;        //当前队列尾部

public:

    //构造函数
    CQueue(int nCount);

    //析构函数
    ~CQueue()
    {
        delete[] m_pData;
    }

    //入列
    void Enqueue(const T& data);
    //出列
    bool Dequeue(T& data);
    
    //判断队满
    bool isFull()
    {
        return (m_nRear + 1) % m_nCount == m_nFront;
    }
    //判断队空
    bool isEmpty()
    {
        return m_nFront == m_nRear;
    }
    
    //遍历输出队列内容
    //注意，如果模板参数传入的为非基础数据类型，则无法使用<<进行流的输出
    void TraverseQueue();

    //清空队列内容
    void ClearQueue();

    //返回Queue的元素个数，即当前队列长度
    int QueueLength()
    {
        return (m_nRear - m_nFront + m_nCount) % m_nCount;
    }
};

template<class T>
CQueue<T>::CQueue(int nCount)
{
    m_pData = new T[nCount];
    m_nCount = nCount;
    m_nFront = m_nRear = 0;    //头尾初始化为0
}

template<class T>
void CQueue<T>::Enqueue(const T& data)
{
    if (!isFull())
    {
        m_pData[m_nRear] = data;
        m_nRear = (m_nRear + 1) % m_nCount;    //队列尾部前移
    }
}

template<class T>
bool CQueue<T>::Dequeue(T& data)
{
    if (isEmpty())
        return false;
    data = m_pData[m_nFront];
    m_pData[m_nFront] = 0;    //出列后该位置数据清零
    m_nFront = (m_nFront + 1) % m_nCount;    //队列头部前移
    return true;
}

template<class T>
void CQueue<T>::TraverseQueue()
{
    int i = m_nFront;
    while (i != m_nRear)
    {
        cout << m_pData[i] << endl;
        i = (i + 1) % m_nCount;
    }
}

template<class T>
void CQueue<T>::ClearQueue()
{
    int i = m_nFront;
    while (i != m_nRear)
    {
        m_pData[i] = 0;
        i = (i + 1) % m_nCount;
    }
    m_nFront = m_nRear = 0;
}

main.cpp

/*******************************************************
* File Name：main.cpp
* Description：用于演示队列数据结构
* Version：V1.0 
* Author：Mengjia 
* Date：2018-06-02 
* Copyright (C)2018, Mengjia
* Others:
* Blog:
*******************************************************/
#include "Queue.h"
#include <iostream>

using namespace std;

int main()
{
    CQueue<int> queue(6);

    int i = 0;
    while (i < 6)
    {
        queue.Enqueue(i++);
    }
    int data = 0;
    queue.Dequeue(data);
    cout << "The first element of queue: " << data << endl;
    queue.Dequeue(data);
    cout << "The second element of queue: " << data << endl;

    cout << "The Length of queue: " << queue.QueueLength() << endl;

    queue.Enqueue(5);
    queue.Enqueue(6);
    cout << "The Length of queue: " << queue.QueueLength() << endl;
    cout << "Output all elements of queue: " << endl;
    queue.TraverseQueue();

    queue.ClearQueue();
    cout << "The Length of queue: " << queue.QueueLength() << endl;
    system("pause");
    return 0;
}

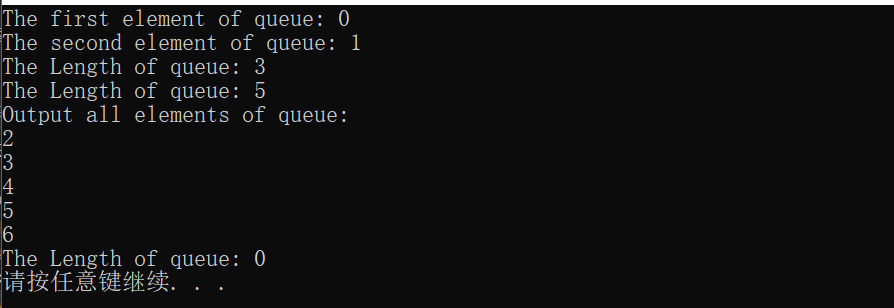
输出结果：