题目描述:
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
旋转数组的特点:
(1)旋转之后的数组实际上可以划分为两个排序的子数组,且前面的子数组的元素都大于或者等于后面子数组的元素。(有一个特例,后面说明!)
(2)最小的元素刚好是这两个数组的分界线。
(3)旋转数组在一定程度上是排序的,因此可以用二分查找法的思路来寻找这个最小的元素。
思路:
(1)设置两个指针,初始状态第一个指针指向前面子数组的第一个元素,第二个指针指向后面子数组的最后一个元素;
(2)找到两个指针的中间元素;
(3)若其大于等于第一个指针指向的元素,则说明其在前面的子数组中,且显然最小元素在中间元素的右边,若其小于等于第二个指针指向的元素,则说明其在后面的子数组中,且显然最小元素在中间元素的左边。如此,便可以缩小搜索范围,最终第一个指针指向前面子数组的最后一个元素,而第二个指针指向后面子数组的第一个元素,它们处于相邻位置,而第二个指针指向的刚好是最小的元素。
以题目举例的数组{3,4,5,1,2}分析,先把第一个指针指向第0个元素,把第二个指针指向第4个元素(如图2.10(a)所示)。位于两个指针中间(在数组中的下标是2)的数字是5,它大于第一个指针指向的数字。因此中间数字5一定位于第一个递增子数组中,并且最小的数组一定位于它的后面。因此可以移动第一个指针让它指向数组的中间(如图2.10(b)所示)。
此时位于这两个指针中间(在数组中的下标是3)的数字是1,它小于第二个指针指向的数字。因此这个中间数字1一定位于第二个递增子数组中,并且最小的数字一定位于它的前面或者它自己就是最小的数字。因此可以移动第二个指针指向两个指针中间的元素,即下标为3的元素(如图2.10(c)所示)。
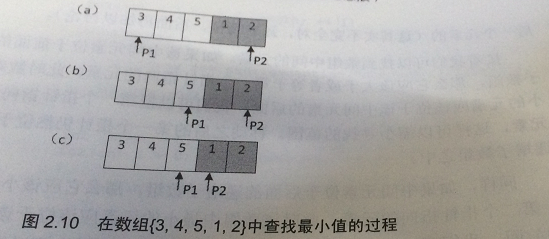
注:旋转数组中包含两个递增排序的子数组,有阴影背景的是第二个子数组。
(a)把P1指向数组的第一个数字,P2指向数组的最后一个数字。由于P1和P2中间的数字5大于P1指向的数字,中间的数字在第一个子数组中。下一步把P1指向中间的数字。
(b)P1和P2中间的数字1小于P2指向的数字,中间的数字在第二个子数组中。下一步把P2指向中间的数字。
(c)P1和P2指向两个相邻的数字,则P2指向的是数组中的最小数字。
此时两个指针的距离是1,表明第一个指针已经指向了第一个递增子数组的末尾,而第二个指针指向第二个递增子数组的开头。第二个子数组的第一个数字就是最小的数字,因此第二个指针指向的数字就是我们查找的结果。
注意两点:
(1)按旋转规则,第一个元素应该是大于或等于最后一个元素的;但也有特例:若把排序数组的前0个元素搬到最后面,及排序数组本身,仍是数组的一个旋转,此时数组中的第一个数字是最小的数字,应该直接返回。
(2)当两个指针指向的数字及它们中间的数字三者相等时,无法判断中间数字位于前面的子数组还是后面的子数组,也就无法移动两个指针来缩小查找的范围,此时只能用顺序查找的方法。
例如:数组{1,0,1,1,1}和数组{1,1,1,0,1}都可看成是递增数组{0,1,1,1,1}的旋转。第一种情况,中间数字位于后面的子数组,第二种情况,中间数字位于前面的子数组。
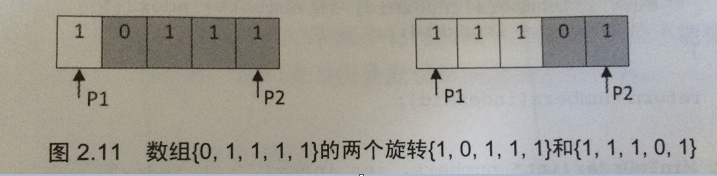
鉴于此,实现的代码如下:
1 /* 2 Time:2016-9-21 17:01:41 3 Author:CodingMengmeng 4 */ 5 #include <iostream> 6 using namespace std; 7 8 int Min(int* data, int length); 9 int MinInOrder(int* data, int index1, int index2); 10 11 int main() 12 { 13 // int nArr1[5] = { 3, 4, 5, 1, 2 }; 14 int nArr1[10] = { 5, 6, 6, 7, 7, 8, 9, 2, 3, 4 }; 15 cout << "the minimum value in nArr1 is " << Min(nArr1,10)<< endl; 16 int nArr2[5] = { 1, 0, 1, 1, 1 }; 17 cout << "the minimum value in nArr2 is " << Min(nArr2, 5) << endl; 18 int nArr3[5] = { 1, 1, 1, 0, 1 }; 19 cout << "the minimum value in nArr3 is " << Min(nArr3, 5) << endl; 20 int nArr4[5] = { 1, 2, 3, 4, 5 }; 21 cout << "the minimum value in nArr4 is " << Min(nArr4, 5) << endl; 22 int* nArr5 = NULL; 23 cout << "the minimum value in nArr5 is " << Min(nArr5, 5) << endl; 24 25 system("pause"); 26 return 0; 27 } 28 29 int Min(int* data, int length) 30 { 31 if (data == NULL || length <= 0) 32 throw new exception("Invalid parameters!"); 33 int index1 = 0; 34 int index2 = length - 1; 35 int indexMid = index1; 36 //若把排序数组的前0个元素搬到最后面,及排序数组本身, 37 //仍是数组的一个旋转,此时数组中的第一个数字是最小的数字,应该直接返回。 38 //显然这种情况不满足while循环,所以直接返回。 39 while (data[index1] >= data[index2]) 40 { 41 /* 42 两个指针的距离是1,表明第一个指针已经指向了第一个递增子数组的末尾, 43 而第二个指针指向第二个递增子数组的开头。 44 第二个子数组的第一个数字就是最小的数字, 45 因此第二个指针指向的数字就是我们查找的结果。 46 */ 47 if (index2-index1==1) 48 { 49 indexMid = index2; 50 break; 51 } 52 indexMid = (index1 + index2) / 2; 53 /* 54 当两个指针指向的数字及它们中间的数字三者相等时, 55 无法判断中间数字位于前面的子数组还是后面的子数组, 56 也就无法移动两个指针来缩小查找的范围,此时只能用顺序查找的方法。 57 */ 58 if (data[index1] == data[index2] && data[indexMid] == data[index1]) 59 return MinInOrder(data, index1, index2); 60 if (data[indexMid] >= data[index1]) 61 index1 = indexMid; 62 else if (data[indexMid] <= data[index2]) 63 index2 = indexMid; 64 } 65 return data[indexMid]; 66 } 67 68 int MinInOrder(int* data, int index1, int index2) 69 { 70 int MinResult = data[index1]; 71 for (int i = index1 + 1; i <= index2; i++) 72 { 73 if (MinResult > data[i]) 74 MinResult = data[i]; 75 } 76 return MinResult; 77 }
运行结果:
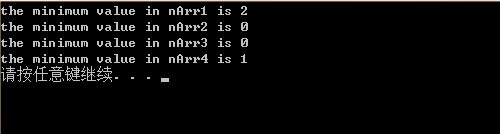
nArr5由于出现异常,在运行结果中未显示!