Polygon
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5024 | Accepted: 2108 |
Description
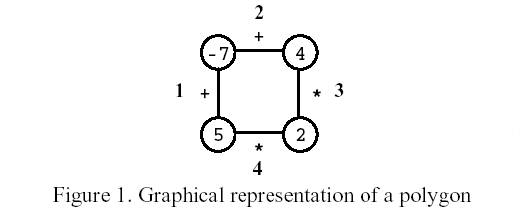
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
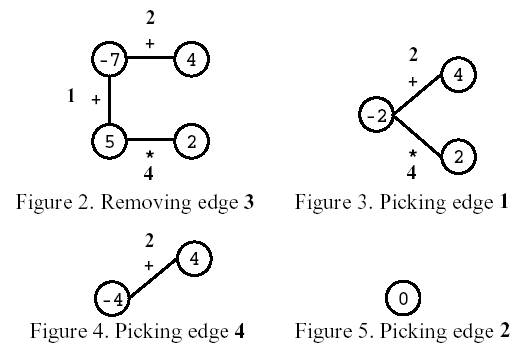
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
Input
Your
program is to read from standard input. The input describes a polygon
with N vertices. It contains two lines. On the first line is the number
N. The second line contains the labels of edges 1, ..., N, interleaved
with the vertices' labels (first that of the vertex between edges 1 and
2, then that of the vertex between edges 2 and 3, and so on, until that
of the vertex between edges N and 1), all separated by one space. An
edge label is either the letter t (representing +) or the letter x
(representing *).
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Output
Your
program is to write to standard output. On the first line your program
must write the highest score one can get for the input polygon. On the
second line it must write the list of all edges that, if removed on the
first move, can lead to a game with that score. Edges must be written in
increasing order, separated by one space.
Sample Input
4 t -7 t 4 x 2 x 5
Sample Output
33 1 2
Source
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<algorithm> 6 using namespace std; 7 8 const int inf=1000000007; 9 const int maxn=20007; 10 11 bool op[maxn]; 12 int maxv[maxn],minv[maxn]; 13 int value[maxn]; 14 bool vis_max[maxn],vis_min[maxn]; 15 int n,ans; 16 int dfs_min(int i,int j); 17 int dfs_max(int i,int j); 18 19 int dfs_min(int i,int j) 20 { 21 int v=100*i+j; 22 if(vis_min[v]) return minv[v]; 23 vis_min[v]=1; 24 if(j-i<=1){ 25 if(j==i) return minv[v]=value[i-1]; 26 else if(!op[i]) return minv[v]=value[i]+value[i-1]; 27 else return minv[v]=value[i]*value[i-1]; 28 } 29 minv[v]=inf; 30 for(int k=i;k<j;k++) 31 { 32 int l=dfs_max(i,k); 33 int r=dfs_max(k+1,j); 34 int ll=dfs_min(i,k); 35 int rr=dfs_min(k+1,j); 36 if(!op[k]) minv[v]=min(minv[v],ll+rr); 37 else minv[v]=min(minv[v],min(l*r,min(ll*rr,min(l*rr,r*ll)))); 38 } 39 return minv[v]; 40 } 41 int dfs_max(int i,int j) 42 { 43 int v=100*i+j; 44 if(vis_max[v]) return maxv[v]; 45 vis_max[v]=1; 46 if(j-i<=1){ 47 if(j==i) return maxv[v]=value[i-1]; 48 else if(!op[i]) return maxv[v]=value[i]+value[i-1]; 49 else return maxv[v]=value[i]*value[i-1]; 50 } 51 maxv[v]=-inf; 52 for(int k=i;k<j;k++) 53 { 54 int l=dfs_max(i,k); 55 int r=dfs_max(k+1,j); 56 int ll=dfs_min(i,k); 57 int rr=dfs_min(k+1,j); 58 if(!op[k]) maxv[v]=max(maxv[v],l+r); 59 else maxv[v]=max(maxv[v],max(l*r,max(ll*rr,max(l*rr,r*ll)))); 60 } 61 return maxv[v]; 62 } 63 int main() 64 { 65 // freopen("in.txt","r",stdin); 66 char c; 67 while(~scanf("%d%*c",&n)){ 68 memset(op,0,sizeof(op)); 69 memset(value,0,sizeof(value)); 70 memset(maxv,0,sizeof(maxv)); 71 memset(minv,0,sizeof(minv)); 72 memset(vis_max,0,sizeof(vis_max)); 73 memset(vis_min,0,sizeof(vis_min)); 74 for(int i=0;i<n;i++) 75 { 76 scanf("%c %d%*c",&c,&value[i]); 77 value[i+n]=value[i]; 78 op[i]=op[i+n]=(c=='x'); 79 } 80 ans=-inf; 81 for(int i=0;i<n;i++) 82 { 83 ans=max(ans,dfs_max(i+1,i+n)); 84 } 85 printf("%d ",ans); 86 bool first=1; 87 for(int i=0;i<n;i++) 88 { 89 if(dfs_max(i+1,i+n)==ans) 90 { 91 if(first){ 92 first=0; 93 printf("%d",i+1); 94 } 95 else printf(" %d",i+1); 96 } 97 } 98 printf(" "); 99 } 100 return 0; 101 }