算法笔记 第13章 专题扩展 学习笔记

13.1 分块思想

问题：给出一个非负整数序列A，元素个数为N，在有可能随时添加或删除元素的情况下，实时查询序列元素第K大，即把序列元素从小到大排序后从左到右的第K个元素。

整体思路是先用O(√N)的时间复杂度找到第K大的元素在哪一块，然后再用O(√N)的时间复杂度在块内找到这个元素，因此单词查询的总时间复杂度为O(√N)。

PAT A1057 Stack (30分)

Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian -- return the median value of all the elements in the stack. With N elements, the median value is defined to be the (-th smallest element if N is even, or (-th if N is odd.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤). Then N lines follow, each contains a command in one of the following 3 formats:

Push key
Pop
PeekMedian

where key is a positive integer no more than 1.

Output Specification:

For each Push command, insert key into the stack and output nothing. For each Pop or PeekMedian command, print in a line the corresponding returned value. If the command is invalid, print Invalid instead.

Sample Input:

17
Pop
PeekMedian
Push 3
PeekMedian
Push 2
PeekMedian
Push 1
PeekMedian
Pop
Pop
Push 5
Push 4
PeekMedian
Pop
Pop
Pop
Pop

Sample Output:

Invalid
Invalid
3
2
2
1
2
4
4
5
3
Invalid

#include<cstdio>
#include<stack>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 100010;
const int sqrN = 350;
int block[sqrN];
int table[maxn];
stack<int> st;
void Push(int x){
    st.push(x);
    block[x/sqrN]++;
    table[x]++;
}
void peekMedian(int K){
    int sum = 0;
    int idx = 0;
    while(sum + block[idx] < K){
        sum += block[idx++];
    }
    int num = idx * sqrN;
    while(sum + table[num] < K){
        sum = sum + table[num++];
    }
    printf("%d
",num);
}
void Pop(){
    int x = st.top();
    st.pop();
    block[x/sqrN]--;
    table[x]--;
    printf("%d
",x);
}
int main(){
    int n;
    char cmd[50];
    memset(block,0,sizeof(block));
    memset(table,0,sizeof(table));
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%s",cmd);
        if(strcmp(cmd,"Push")==0){
            int x;
            scanf("%d",&x);
            Push(x);
        }else if(strcmp(cmd,"Pop") == 0){
            if(st.empty() == true){
                printf("Invalid
");
            }else{
                Pop();
            }
        }else{
            if(st.empty() == true){
                printf("Invalid
");
            }else{
                int K = st.size();
                if(K % 2==0){
                    K = K/2;
                }else{
                    K = (K + 1)/2;
                }
                peekMedian(K);
            }
        }
    }
    return 0;
}

13.2 树状数组（BIT）

13.2.1 lowbit运算

lowbit(x) = x & (-x)

lowbit(x)也可以理解为能整除x的最大2的幂次

13.2.2 树状数组及其应用

树状数组其实仍然是一个数组，存放的是在i号位之前lowbit(i)个整数之和。

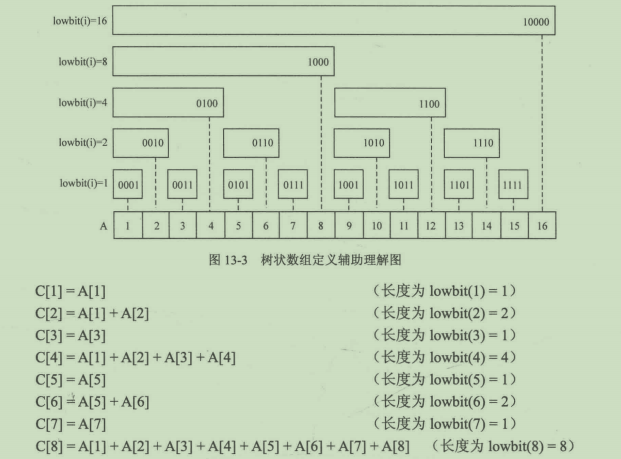
C[x] = A[x - lowbit(x) + 1] +......A[x]

SUM(1,x) = A[1] + .........+ A[x]

　　　　  = A[1] + .......+ A[x - lowbit(x)] + A[x - lowbit(x) +1] + ......+ A[x]

　　　　  = SUM(1,x-lowbit(x)) + C[x]

//getSum函数返回前x个整数之和 
int getSum(int x){
    int sum = 0; //记录和
    for(int i = x; i > 0; i -= lowbit(i))){    //注意是i > 0而不是i >=0 
        sum += c[i]; //累计c[i]，然后把问题缩小为SUM(1,i-lowbit(i)) 
    } 
    return sum; //返回和 
}

//update函数将第x个整数加上v 
void update(int x,int v){
    for(int i = x;i<=N;i += lowbit(i)){    //注意i必须能够取到v 
        c[i] += v;//让c[i]加上v，然后让c[i + lowbit(i)]加上v 
    } 
}

树状数组经典应用：给定一个有N个正整数的序列A（N <= 10^5,A[i] <= 10^5）,对序列中的每个数，求出序列中它左边比它小的数的个数。

#include<cstdio> 
#include<cstring>
const int maxn = 100010;
#define lowbit(i) ((i)&(-i))
int c[maxn];
//getSum函数返回前x个整数之和 
int getSum(int x){
    int sum = 0; //记录和
    for(int i = x; i > 0; i -= lowbit(i)){    //注意是i > 0而不是i >=0 
        sum += c[i]; //累计c[i]，然后把问题缩小为SUM(1,i-lowbit(i)) 
    } 
    return sum; //返回和 
}
//update函数将第x个整数加上v 
void update(int x,int v){
    for(int i = x;i<=maxn;i += lowbit(i)){    //注意i必须能够取到v 
        c[i] += v;//让c[i]加上v，然后让c[i + lowbit(i)]加上v 
    } 
}
int main(){
    int n,x;
    scanf("%d",&n);
    memset(c,0,sizeof(c));
    for(int i = 0; i < n ;i++){
        scanf("%d",&x);
        update(x,1);
        printf("%d
",getSum(x-1));
    }
    return 0;
}