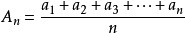如何衡量离散程度
衡量指标
离散系数,离散系数又称变异系数,是统计学当中的常用统计指标,主要用于比较不同水平的变量数列的离散程。
离散系数指标有:全距(极差)系数、平均差系数、方差系数和标准差系数等。常用的是标准差系数,用CV(Coefficient of Variance)表示。
标准差系数
CV(Coefficient of Variance):标准差与均值的比率。总体标准差系数的计算公式为:
Vσ= σ/ x ×100%,Vσ为标准差系数;σ为标准差;x 为平均数。
标准差
标准差(Standard Deviation),在概率统计中最常使用作为统计分布程度(statistical dispersion)上的测量。标准差定义是总体各单位标准值与其平均数离差平方的算术平均数的平方根。它反映组内个体间的离散程度。
公式为如下,N为数据数量,xi为第i个数据,μ为均值:

简单来说,标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
均值
算术平均数是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。