本章博文用来使用二叉树的知识来对文件进行压缩与解压缩,这种压缩专门针对 ASCII 码(英文及英文标点)的压缩技术,希望这篇博文能帮助到正在学习或者想要练习二叉树方面知识的同学!!!
开篇我来介绍一下什么是二叉树:
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”。(示意图如下)
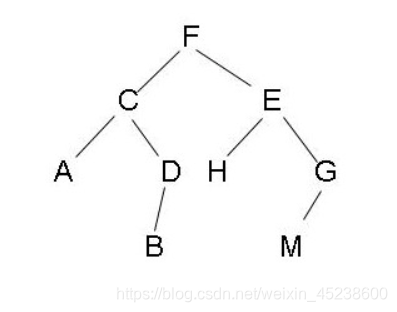
如上图所示,二叉树的“度”小于等于2
那么,什么是哈夫曼压缩呢?这里,我先引进一个知识点——“哈夫曼编码”:
我们为每一种在文件中出现的字符根据其出现频度赋予相应的哈夫曼编码
举个简单的例子,我来提供一个哈夫曼树:
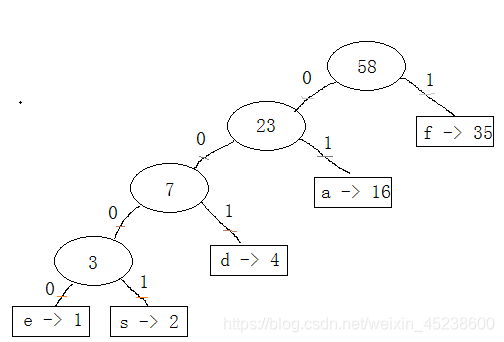
如上图:我们将每次最小的两个节点分别作为“左孩子”和“右孩子”
而存储有效数据的节点我们称之为叶子节点,没有存储有效数据的节点我么称之为根节点(如上图存储58,23,7,3的节点)
在这里,我们令向左为0,向右为1,从根出发,那么,相应的字母及其的哈夫曼编码如下:
f:1
a:01
d:001
e:0000
s:0001
所以,我们进行哈夫曼压缩的步骤其实也就可以总结为如下:
1.统计该文件中出现的不同字节及其频度;
2.根据上述统计数据,构造哈夫曼树;
3.根据上述哈夫曼树,构造每一个字节的哈夫曼编码;
4.将文件中的字节,转换成相应的哈夫曼编码,并将其输出。
所以,在知道了大致的步骤之后,我们就开始编写相应代码:
首先是编写我的博文中几乎每篇都会出现的"mec.h"文件:
#ifndef _MEC_H_
#define _MEC_H_
typedef unsigned char boolean;
typedef boolean u8;
#define TRUE 1
#define FALSE 0
#define SET(v, i) (v |= (1 << ((i) ^ 7)))
#define CLR(v, i) (v &= ~(1 << ((i) ^ 7)))
#define GET(v, i) (((v) & (1 << ((i) ^ 7))) != 0)
#endif
之后是定义一个结构体,它用来存放字符及其相应的频度:
typedef struct FREQ{
unsigned char ch;
int freq;
}FREQ;
那么,接下来的步骤就是编写查找文件中的字符种类以及相应的频度函数:
因为我们要从一个文件中查找,所以,参数一定是文件名;
而我们最终要得到的结果是用结构体数组存放目标结构体,所以,这个函数的返回值就是该结构体数组的指针。
但是,我们还需要在遍历目标文件后返回文件中的字符种类地总数,以便我们之后遍历结构体数组,但是,我们已经确定了返回值,所以,我们就传递该变量的首地址,用指针变量作为参数的形式改变那个变量的值
那么,相应代码段如下:
FREQ *getFreq(const char *fileName, int *chCount) {
FILE *fp;
int ch;
FREQ *freq = NULL;
int bytes[256] = {0};
int index;
int t = 0;
fp = fopen(fileName, "rb");
ch = fgetc(fp);
while (!feof(fp)) {
++bytes[ch];
ch = fgetc(fp);
}
*chCount = 0;
for (index = 0; index < 256; index++) { //上两个循环的目的是:计算所有字符种类计算
if (bytes[index] != 0) {
++*chCount;
}
}
freq = (FREQ *) calloc(sizeof(FREQ), *chCount);
for (index = 0; index < 256; index++) { //这个循环的目的是为储存相应字符信息的结构体(即存储字符种类和频度的结构体)赋值
if (bytes[index] != 0) {
freq[t].ch = index;
freq[t].freq = bytes[index];
t++;
}
}
fclose(fp);
return freq;
}
接下来要构建哈夫曼树的话,就要用一个新的结构体来存放各节点的信息,而哈夫曼树其实也是一种二叉树,所以,我们编写如下结构体:
typedef struct HUFF_TAB {
FREQ freq; //这个成员用于存储该字符的频度以及ASCII码
int leftChild; //若该节点没有左孩子赋值为-1,因为频度不可能是负数
int rightChild; //若该节点没有左孩子赋值为-1,理由如上
boolean isVisited; //这个成员用于表示该节点是否被访问过,用于之后部分函数的部分功能
char *code; //这个成员用于存储该字符的哈夫曼编码
}HUFF_TAB;
那么,结构体我们构建好了,并且查找了该文件中的字符总数和相应频度,按照我们之前列好的步骤,接下来,我们要做的是根据我们之前查找出来的数据,构建哈夫曼树:
现在我们来编写初始化哈夫曼树的函数:
因为我们要得到的结果是表示哈夫曼树的结构体,所以返回值为HUFF_TAB *类型,而根据我们已知,我们可以将叶子结点完善,至于根节点,因为要进行一些操作才能完善,所以,为了代码直观可读性,我们之后编写一个函数专门用来处理根节点。所以,本函数代码如下:
HUFF_TAB *initHuffTab(const FREQ *freq, int *huftabIndex, int alphaCount) {
HUFF_TAB *huffTab = NULL;
int index = 0;
huffTab = (HUFF_TAB *) calloc(sizeof(HUFF_TAB), 2*alphaCount - 1);
for (; index < alphaCount; index++) {
huffTab[index].freq.ch = freq[index].ch;
huffTab[index].freq.freq = freq[index].freq;
huffTab[index].isVisited = FALSE;
huffTab[index].leftChild = huffTab[index].rightChild = -1;
huffTab[index].code = (char *) calloc(sizeof(char), alphaCount);
huftabIndex[freq[index].ch] = index; //这里是用到了之前本人博文《内存对齐模式》中讲过的内存页式管理模式的思想
}
return huffTab;
}
那么,在这里我们编写处理根节点的函数:
同样地,编写前,我们要考虑函数的参数以及返回值:
因为我们要对于结构体数组中查找到的数据进行操作,所以我们要传递的参数为结构体数组类型(即:HUFF_TAB *类型)以及字符种类总数
而我们要得到的结果是给该结构体赋值,所以,这个函数的返回值为void.
那么,相应代码段如下:
void createHuffTree(HUFF_TAB *huffTab, int count) {
int leftChild;
int rightChild; //这里对这两个变量的声明做解释:若直接用scanf函数为结构体成员赋初值,就可能会出现错误,所以我们将要赋的值赋给同类型变量,再将此变量的值赋给该成员
int i; //当然,我们学到现在的程度,看到类似于i,j,k等无特殊意义的函数声明,首先应该想到的是用于循环
int t = count; //因为我们要对于数组进行操作,但是用于循环结束标志的count不能发生改变,所以,设置此变量来同时满足这两个要求
for (i = 0; i < count-1; i++) { //根据先人的推导,我们发现,在哈夫曼树中,根节点数比叶子节点数少一个
leftChild = findMinFreq(huffTab, count + i); //我们这里用左孩子存当前频度排序中最小的字符的频度(这里用左孩子存最小不是硬性要求)
rightChild = findMinFreq(huffTab, count + i); //这样操作右孩子存的频度一定不会比左孩子村的频度小
huffTab[t].freq.ch = '#'; //这里是我们假设所有“根节点”的ch为字符#
huffTab[t].freq.freq = huffTab[leftChild].freq.freq + huffTab[rightChild].freq.freq;
huffTab[t].leftChild = leftChild;
huffTab[t].rightChild = rightChild;
huffTab[t].isVisited = FALSE;
huffTab[t].code = NULL; //因为我们不知道该字符在哈夫曼树的位置,所以我们先令所有的编码都为0,在后面单独写一个函数为所有存储字符信息的结构体赋值
t++;
}
}
那么,我们接下来编写上个函数中所用到的函数——查找最小频度的孩子节点的频度函数:
int findMinFreq(HUFF_TAB *huffTab, int count) {
int minIndex = -1;
int index;
for (index = 0; index < count; index++) {
if (!huffTab[index].isVisited && (
minIndex == -1 || huffTab[index].freq.freq < huffTab[minIndex].freq.freq)) {
minIndex = index;
}
}
huffTab[minIndex].isVisited = TRUE;
return minIndex;
}
根据我们以往的编程经验,我们编写了生成哈夫曼树的函数,就要立刻想到要去编写销毁哈夫曼树的函数,这样的思考方式可以避免出现很多错误,例如在这个程序中,就可以避免造成内存泄漏。
那么,现在,我们来编写销毁哈夫曼树的函数:
void destoryHuffTab(HUFF_TAB *huffTab, int alphaCount) {
int i;
for (i = 0; i < alphaCount; i++) {
free(huffTab[i].code);
}
free(huffTab);
}
哈夫曼树我们已经构建好了,接下来我们只需要将各字符通过哈夫曼树转换为相应的哈夫曼编码即可,那么,我们现在来编写构建哈夫曼编码的函数:
void createHuffCode(HUFF_TAB *huffTab, int root, int index, char *str) {
if (huffTab[root].leftChild == -1) {
str[index] = 0; //我们令根节点的的code为0
strcpy(huffTab[root].code, str);
} else {
str[index] = '0';
createHuffCode(huffTab, huffTab[root].leftChild, index+1, str);
str[index] = '1';
createHuffCode(huffTab, huffTab[root].rightChild, index+1, str);
}
}
这个函数是个递归函数,也是整个程序的核心部分,由恩师微易码教主提供,具体验证过程需要读者们自己进行。
那么,现在我们要进行的操作就是将原文件的每个字符内容转换为相应的哈夫曼编码,那么,我们现在来编写转换原文件为哈夫曼编码构成的新文件的函数:
在此之前,我们需要模仿其他文件的存储方式,给新文件加一个“文件头”,所以,我们来定义一个结构体来表示这个“文件头”:
typedef struct MEC_HUFF_HEAD {
char flag[3]; //这里的头是用于区分我们的压缩文件用的
int alphaCount; //这个成员用来存储总原文件的字符种类数
int bitCount; //这个成员,用于存储压缩之后的编码的总位数(因为一个字节是8位,若我们转换之后的长度不是8的倍数,就会由垃圾数据补齐8位,所以我们所读取的最后一个字节可能不全是原文件压缩后所得的)
u8 unused[5]; //这个成员是我们用于填文件头长度量用的(因为我们定义的文件头长度为16个字节,这样的文件用UE打开的话,正好长度占一行,比较美观)
}MEC_HUFF_HEAD;
void codding(const char *sourceFileName, const char *targetFileName,
FREQ *freq, int alphaCount,
HUFF_TAB *huffTab, int *huftabIndex) {
FILE *in;
FILE *out;
int ch;
char *code;
int i;
u8 byte;
int byteIndex = 0;
MEC_HUFF_HEAD head = {0};
head.flag[0] = 'M';
head.flag[1] = 'E';
head.flag[2] = 'C'; //我们定义前三个字符长度存储MEC,用于解压缩时的判断
head.alphaCount = alphaCount;
head.bitCount = getBitCount(huffTab, alphaCount); //这里的操作比较麻烦,我们之后专门编写一个函数来实现
in = fopen(sourceFileName, "rb"); //用于读取原文件所用的指针
out = fopen(targetFileName, "wb"); //用于向目标文件中写入哈夫曼编码的指针
fwrite(&head, sizeof(MEC_HUFF_HEAD), 1, out);
fwrite(freq, sizeof(FREQ), alphaCount, out);
ch = fgetc(in);
while (!feof(in)) {
code = huffTab[huftabIndex[ch]].code;
for (i = 0; code[i]; i++) {
code[i] == '0' ? CLR(byte, byteIndex) : SET(byte, byteIndex); //这里的CLR和SET是二进制位水平上的置0和置一的宏,在我们编写的"mec.h"头文件中,具体讲解请观看本人的博文——《位运算相关详解》
++byteIndex;
if (byteIndex >= 8) {
byteIndex = 0;
fputc((int) byte, out);
}
}
ch = fgetc(in);
}
if (byteIndex != 0) {
fputc((int) byte, out);
}
fclose(in);
fclose(out);
}
在这里,我们的压缩操作就基本完成了,下面我来总结下压缩相关的程序:
mec.h:
#ifndef _MEC_H_
#define _MEC_H_
typedef unsigned char boolean;
typedef boolean u8;
#define TRUE 1
#define FALSE 0
#define SET(v, i) (v |= (1 << ((i) ^ 7)))
#define CLR(v, i) (v &= ~(1 << ((i) ^ 7)))
#define GET(v, i) (((v) & (1 << ((i) ^ 7))) != 0)
#endif
huffman.h:
#pragma pack(push) //接下来的所有#pragma可以看作是为了取消内存对齐模式而编写的,这里不对原理进行讲解
#pragma pack(1)
#ifndef _HUFFMAN_H_
#define _HUFFMAN_H_
#include "mec.h"
typedef struct FREQ {
u8 ch;
int freq;
}FREQ;
typedef struct HUFF_TAB {
FREQ freq;
int leftChild;
int rightChild;
boolean isVisited;
char *code;
}HUFF_TAB;
typedef struct MEC_HUFF_HEAD {
char flag[3];
int alphaCount;
int bitCount;
u8 unused[5];
}MEC_HUFF_HEAD;
boolean isFileExist(const char *fileName);
void showFreq(FREQ *freq, int count);
HUFF_TAB *initHuffTab(const FREQ *freq, int *huftabIndex, int alphaCount);
void createHuffTree(HUFF_TAB *huffTab, int count);
void createHuffCode(HUFF_TAB *huffTab, int root, int index, char *str);
void destoryHuffTab(HUFF_TAB *huffTab, int alphaCount);
void showHuffTab(HUFF_TAB *huffTab, int alphaCount);
#endif
#pragma pack(pop)
huffman.c:
#include <stdio.h>
#include <malloc.h>
#include <string.h>
#include "mec.h"
#include "huffman.h"
static int findMinFreq(HUFF_TAB *huffTab, int count);
HUFF_TAB *initHuffTab(const FREQ *freq, int *huftabIndex, int alphaCount) {
HUFF_TAB *huffTab = NULL;
int index = 0;
huffTab = (HUFF_TAB *) calloc(sizeof(HUFF_TAB), 2*alphaCount - 1);
for (; index < alphaCount; index++) {
huffTab[index].freq.ch = freq[index].ch;
huffTab[index].freq.freq = freq[index].freq;
huffTab[index].isVisited = FALSE;
huffTab[index].leftChild = huffTab[index].rightChild = -1;
huffTab[index].code = (char *) calloc(sizeof(char), alphaCount);
huftabIndex[freq[index].ch] = index;
}
return huffTab;
}
void createHuffCode(HUFF_TAB *huffTab, int root, int index, char *str) {
if (huffTab[root].leftChild == -1) {
str[index] = 0;
strcpy(huffTab[root].code, str);
} else {
str[index] = '0';
createHuffCode(huffTab, huffTab[root].leftChild, index+1, str);
str[index] = '1';
createHuffCode(huffTab, huffTab[root].rightChild, index+1, str);
}
}
void createHuffTree(HUFF_TAB *huffTab, int count) {
int leftChild;
int rightChild;
int i;
int t = count;
for (i = 0; i < count-1; i++) {
leftChild = findMinFreq(huffTab, count + i);
rightChild = findMinFreq(huffTab, count + i);
huffTab[t].freq.ch = '#';
huffTab[t].freq.freq = huffTab[leftChild].freq.freq + huffTab[rightChild].freq.freq;
huffTab[t].leftChild = leftChild;
huffTab[t].rightChild = rightChild;
huffTab[t].isVisited = FALSE;
huffTab[t].code = NULL;
t++;
}
}
int findMinFreq(HUFF_TAB *huffTab, int count) {
int minIndex = -1;
int index;
for (index = 0; index < count; index++) {
if (!huffTab[index].isVisited && (
minIndex == -1 || huffTab[index].freq.freq < huffTab[minIndex].freq.freq)) {
minIndex = index;
}
}
huffTab[minIndex].isVisited = TRUE;
return minIndex;
}
void destoryHuffTab(HUFF_TAB *huffTab, int alphaCount) {
int i;
for (i = 0; i < alphaCount; i++) {
free(huffTab[i].code);
}
free(huffTab);
}
huff.c:
#include <stdio.h>
#include <string.h>
#include <malloc.h>
#include "mec.h"
#include "huffman.h"
FREQ *getFreq(const char *fileName, int *chCount);
void codding(const char *sourceFileName, const char *targetFileName,
FREQ *freq, int alphaCount,
HUFF_TAB *huffTab, int *huftabIndex);
int getBitCount(HUFF_TAB *huffTab, int alphaCount);
int getBitCount(HUFF_TAB *huffTab, int alphaCount) {
int i;
int sum = 0;
for (i = 0; i < alphaCount; i++) {
sum += strlen(huffTab[i].code) * huffTab[i].freq.freq;
}
return sum;
}
void codding(const char *sourceFileName, const char *targetFileName,
FREQ *freq, int alphaCount,
HUFF_TAB *huffTab, int *huftabIndex) {
FILE *in;
FILE *out;
int ch;
char *code;
int i;
u8 byte;
int byteIndex = 0;
MEC_HUFF_HEAD head = {0};
head.flag[0] = 'M';
head.flag[1] = 'E';
head.flag[2] = 'C';
head.alphaCount = alphaCount;
head.bitCount = getBitCount(huffTab, alphaCount);
in = fopen(sourceFileName, "rb");
out = fopen(targetFileName, "wb");
fwrite(&head, sizeof(MEC_HUFF_HEAD), 1, out);
fwrite(freq, sizeof(FREQ), alphaCount, out);
ch = fgetc(in);
while (!feof(in)) {
code = huffTab[huftabIndex[ch]].code;
for (i = 0; code[i]; i++) {
code[i] == '0' ? CLR(byte, byteIndex) : SET(byte, byteIndex);
++byteIndex;
if (byteIndex >= 8) {
byteIndex = 0;
fputc((int) byte, out);
}
}
ch = fgetc(in);
}
if (byteIndex != 0) {
fputc((int) byte, out);
}
fclose(in);
fclose(out);
}
FREQ *getFreq(const char *fileName, int *chCount) {
FILE *fp;
int ch;
FREQ *freq = NULL;
int bytes[256] = {0};
int index;
int t = 0;
fp = fopen(fileName, "rb");
ch = fgetc(fp);
while (!feof(fp)) {
++bytes[ch];
ch = fgetc(fp);
}
*chCount = 0;
for (index = 0; index < 256; index++) {
if (bytes[index] != 0) {
++*chCount;
}
}
freq = (FREQ *) calloc(sizeof(FREQ), *chCount);
for (index = 0; index < 256; index++) {
if (bytes[index] != 0) {
freq[t].ch = index;
freq[t].freq = bytes[index];
t++;
}
}
fclose(fp);
return freq;
}
int main(int ac, char **str) {
char sourceFileName[1024];
char targetFileName[1024];
FREQ *freq;
HUFF_TAB *huffTab = NULL;
int alphaCount = 0;
char string[256] = {0};
int huftabIndex[256] = {0};
if (ac != 3) {
printf("用法:test <源文件> <目标文件名><br>");
return;
}
strcpy(sourceFileName, str[1]);
strcpy(targetFileName, str[2]);
strcat(targetFileName, ".mecHuf");
if (!isFileExist(sourceFileName)) {
printf("源文件[%s]不存在!
", sourceFileName);
return;
}
freq = getFreq(sourceFileName, &alphaCount);
huffTab = initHuffTab(freq, huftabIndex, alphaCount);
createHuffTree(huffTab, alphaCount);
createHuffCode(huffTab, 2*alphaCount - 2, 0, string);
codding(sourceFileName, targetFileName, freq, alphaCount, huffTab, huftabIndex);
free(freq);
destoryHuffTab(huffTab, alphaCount);
return 0;
}
一共编写了4个文件,所以要用LINUX知识的操作或者命令行操作进行多文件联编,这里也不进行详解。
既然我们编写了哈夫曼压缩的代码,当然就要编写哈夫曼解压缩的相关程序:
那么,要做的第一步是读取文件头,判别该文件是否为我们所需的哈夫曼压缩文件,这两个函数的代码如下:
MEC_HUFF_HEAD readFileType(const char *sourceFileName) {
FILE *fp;
MEC_HUFF_HEAD head = {0};
fp = fopen(sourceFileName, "rb");
fread(&head, sizeof(MEC_HUFF_HEAD), 1, fp);
fclose(fp);
return head;
}
boolean isMecHuffFile(MEC_HUFF_HEAD head) {
return head.flag[0] == 'M' && head.flag[1] == 'E' && head.flag[2] == 'C';
}
因为我们之后要进行解压的话,也要还原压缩文件为哈夫曼树,再还原为哈夫曼编码,所以,和哈夫曼压缩的程序中的代码一样,我们需要得到文件中所有字符种类及其频度,所以我们用到上面的代码:
FREQ *getFreq(const char *sourceFileName, MEC_HUFF_HEAD head) {
FREQ *freq = NULL;
FILE *fp;
int index;
freq = (FREQ *) calloc(sizeof(FREQ), head.alphaCount);
fp = fopen(sourceFileName, "rb");
fseek(fp, sizeof(MEC_HUFF_HEAD), SEEK_SET);
fread(freq, sizeof(FREQ), head.alphaCount, fp);
return freq;
}
现在,我们来编写哈夫曼解压缩程序的核心函数——解压缩函数:
我们现在来详解这个函数:
因为我们不需要返回主函数任何变量,所以,返回值类型为void,
至于函数的参数,首先要想到的是压缩文件名和解压后的文件名,文件头,字符种类总数和总位数,相关代码如下:
void decodding(const char *sourceFileName, const char *targetFileName,
HUFF_TAB *huffTab, int alphaCount, int bitCount) {
FILE *in;
FILE *out;
int ch;
int count = 0;
int root = 2*alphaCount - 2;
int bitIndex = 8;
in = fopen(sourceFileName, "rb");
out = fopen(targetFileName, "wb");
fseek(in, sizeof(MEC_HUFF_HEAD) + alphaCount * sizeof(FREQ), SEEK_SET);
while (count <= bitCount) {
if (huffTab[root].leftChild == -1) {
fputc(huffTab[root].freq.ch, out);
root = 2*alphaCount - 2;
if (count >= bitCount) {
break;
}
} else {
if (bitIndex >= 8) {
ch = fgetc(in);
bitIndex = 0;
}
if (GET(ch, bitIndex) == 0) {
root = huffTab[root].leftChild;
} else {
root = huffTab[root].rightChild;
}
count++;
bitIndex++;
}
}
fclose(in);
fclose(out);
}
总结下哈夫曼解压缩的代码,结果如下:
#include <stdio.h>
#include <string.h>
#include <malloc.h>
#include "mec.h"
#include "huffman.h"
MEC_HUFF_HEAD readFileType(const char *sourceFileName);
boolean isMecHuffFile(MEC_HUFF_HEAD head);
FREQ *getFreq(const char *sourceFileName, MEC_HUFF_HEAD head);
void decodding(const char *sourceFileName, const char *targetFileName,
HUFF_TAB *huffTab, int alphaCount, int bitCount);
void decodding(const char *sourceFileName, const char *targetFileName,
HUFF_TAB *huffTab, int alphaCount, int bitCount) {
FILE *in;
FILE *out;
int ch;
int count = 0;
int root = 2*alphaCount - 2;
int bitIndex = 8;
in = fopen(sourceFileName, "rb");
out = fopen(targetFileName, "wb");
fseek(in, sizeof(MEC_HUFF_HEAD) + alphaCount * sizeof(FREQ), SEEK_SET);
while (count <= bitCount) {
if (huffTab[root].leftChild == -1) {
fputc(huffTab[root].freq.ch, out);
root = 2*alphaCount - 2;
if (count >= bitCount) {
break;
}
} else {
if (bitIndex >= 8) {
ch = fgetc(in);
bitIndex = 0;
}
if (GET(ch, bitIndex) == 0) {
root = huffTab[root].leftChild;
} else {
root = huffTab[root].rightChild;
}
count++;
bitIndex++;
}
}
fclose(in);
fclose(out);
}
FREQ *getFreq(const char *sourceFileName, MEC_HUFF_HEAD head) {
FREQ *freq = NULL;
FILE *fp;
int index;
freq = (FREQ *) calloc(sizeof(FREQ), head.alphaCount);
fp = fopen(sourceFileName, "rb");
fseek(fp, sizeof(MEC_HUFF_HEAD), SEEK_SET);
fread(freq, sizeof(FREQ), head.alphaCount, fp);
return freq;
}
boolean isMecHuffFile(MEC_HUFF_HEAD head) {
return head.flag[0] == 'M' && head.flag[1] == 'E' && head.flag[2] == 'C';
}
MEC_HUFF_HEAD readFileType(const char *sourceFileName) {
FILE *fp;
MEC_HUFF_HEAD head = {0};
fp = fopen(sourceFileName, "rb");
fread(&head, sizeof(MEC_HUFF_HEAD), 1, fp);
fclose(fp);
return head;
}
int main(int argc, char **argv) {
char sourceFileName[1024];
char targetFileName[1024];
MEC_HUFF_HEAD head;
FREQ *freq = NULL;
HUFF_TAB *huffTab = NULL;
int alphaCount = 0;
char string[256] = {0};
int huftabIndex[256] = {0};
if (argc != 3) {
printf("用法: dehuff <源文件名称> <目标文件名称> <br>");
return 0;
}
strcpy(sourceFileName, argv[1]);
strcpy(targetFileName, argv[2]);
if (!isFileExist(sourceFileName)) {
printf("源文件[%s]不存在!
", sourceFileName);
return 0;
}
head = readFileType(sourceFileName);
if (!isMecHuffFile(head)) {
printf("不可识别的格式!
");
return 0;
}
alphaCount = head.alphaCount;
freq = getFreq(sourceFileName, head);
huffTab = initHuffTab(freq, huftabIndex, alphaCount);
createHuffTree(huffTab, alphaCount);
createHuffCode(huffTab, 2*alphaCount - 2, 0, string);
decodding(sourceFileName, targetFileName, huffTab, alphaCount, head.bitCount);
destoryHuffTab(huffTab, alphaCount);
free(freq);
return 0;
}
那么,在上面的编写过程中我们提到的有些知识点是通过以下两篇博文学到的:
《详解 位运算》:位运算知识
《内存对齐模式 —— 原理讲解》:内存页式管理思想