Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.
Example 1:
Input: 2 Output: 1 Explanation: 2 = 1 + 1, 1 × 1 = 1.Example 2:
Input: 10 Output: 36 Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.
Note: You may assume that n is not less than 2 and not larger than 58.
整数拆分。题意是给一个整数n,请你把它拆分成2个或者更多个正整数,使得拆分下来的数字之间的乘积是最大的。
我简单试了几个例子,比如2,只能拆成1x1 = 1,这没什么可说的;3可以拆成1x1x1 = 1但是这毫无意义,拆成1x2 = 2的结果都比它大;4可以拆成1x3 = 3或者2x2 = 4;5可以拆成1x4 = 5或者2x3 = 6;6可以拆成1x5 = 5或者2x4 = 8;7可以拆成1x6 = 6或者2x2x3 = 12;8可以拆成1x7 = 7或者2x2x2x2 = 16。
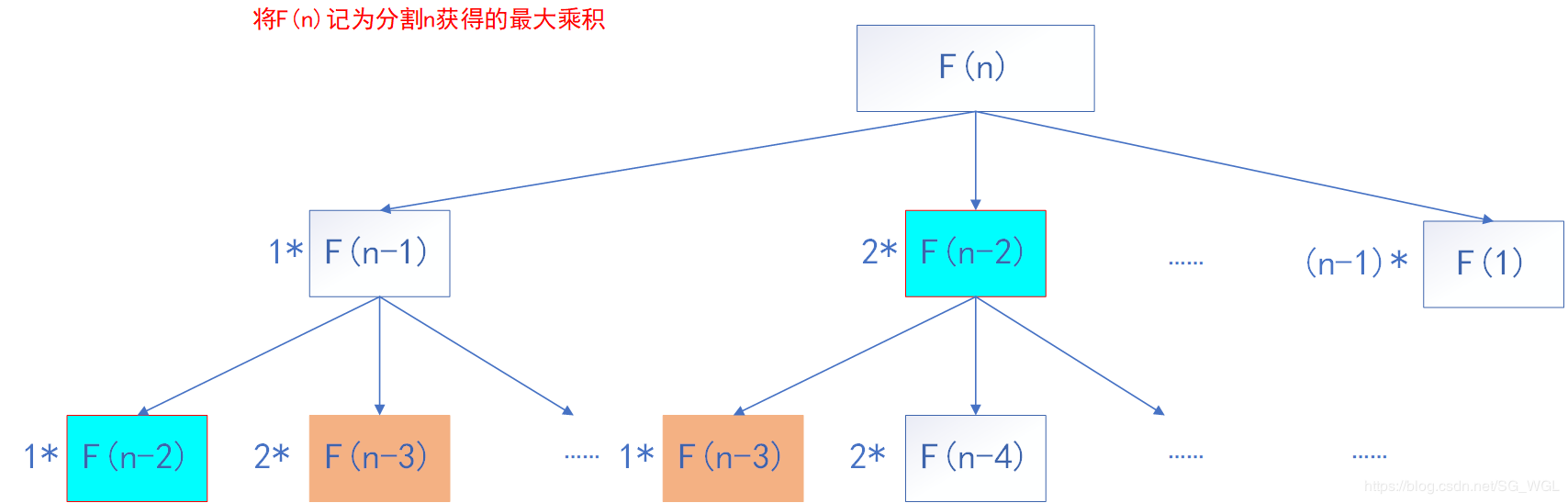
注意到为了要使乘积更大,首先1xN这种情况肯定不会使乘积更大,那么就试着试一些因数比1大的情形。你会发现乘积比较大的结果,因数总是往2和3上靠近,因为这样可以使得因子更多。同时发现一个数字被分解后得到的最大乘积既然最后总是往2和3靠近,那么这里面就一定有重复计算。我这里找个一张截图解释数字如何拆分,实际上这个题也是可以用动态规划做的。
动态规划的定义是dp[i]表示数字i被拆分后能得到的最大乘积。转移方程是dp[i] = k * (i - k) 或者dp[i] = dp[k] * dp[i - k],0 < k < i
意思是dp值有可能是一个数被拆解成两个数字(小于6的情况),或者是这个数字可以被拆解成更多个因子,只不过是后面第二种情况dp[k] * dp[i - k]事实上是对之前的答案有储存。
时间O(n)
空间O(n)
Java实现
1 class Solution { 2 public int integerBreak(int n) { 3 int[] dp = new int[n + 1]; 4 for (int i = 1; i <= n; i++) { 5 for (int j = 1; j < i; j++) { 6 dp[i] = Math.max(dp[i], (i - j) * j); 7 dp[i] = Math.max(dp[i], dp[j] * (i - j)); 8 } 9 } 10 return dp[n]; 11 } 12 }