Problem Description
Dear Liao
I never forget the moment I met with you. You carefully asked me: "I have a very difficult problem. Can you teach me?". I replied with a smile, "of course". You replied:"Given a matrix, I randomly choose a sub-matrix, what is the expectation of the number of different numbers it contains?"
Sincerely yours,
Guo
Input
The first line of input contains an integer T(T≤8) indicating the number of test cases.
Each case contains two integers, n and m (1≤n, m≤100), the number of rows and the number of columns in the grid, respectively.
The next n lines each contain m integers. In particular, the j-th integer in the i-th of these rows contains g_i,j (0≤ g_i,j < n*m).
Output
Each case outputs a number that holds 9 decimal places.
Sample Input
1
2 3
1 2 1
2 1 2
Sample Output
1.666666667
Hint
6(size = 1) + 14(size = 2) + 4(size = 3) + 4(size = 4) + 2(size = 6) = 30 / 18 = 6(size = 1) + 7(size = 2) + 2(size = 3) + 2(size = 4) + 1(size = 6)
题意:
给出一个n*m(1<=n,m<=100)的矩阵,矩阵中的每一个元素有一个颜色值ai(0<=ai<=10000),现在定义一个子矩阵的value为该子矩阵中不同颜色的数量,求所有子矩阵value的期望。
分析:
期望(也就相当于均值)=所有子矩阵的value之和 / 子矩阵个数。
首先解决子矩阵有多少个,二重循环枚举子矩形右下角的点(i,j),那么子矩阵左上角的点一定在(0,0)-(i,j)这个矩阵里,所以有i*j种。
还可以直接代公式:(n(n+1)(m+1)*m)/4
接下来我们讲重点:显然要每个颜色单独考虑,在考虑颜色i的时候,把颜色i的点看作关键点,求出 至少包含一个关键点的子矩阵个数。现在的问题是我们如何不重复不遗漏的统计个数。
先排个序(行号升序,列号升序)。把每个合法的矩阵算在序最小的那个关键点头上,这样就可以保证不重复,不遗漏。那么我们再找包含第一个关键点的矩阵的时候,显然没有任何限制,只需要包含这个点就行了。找第二个关键点的矩阵的时候,不能包含第一个点……找第i个关键点决定的矩阵的时候,不能包含1..i-1这i-1个点。
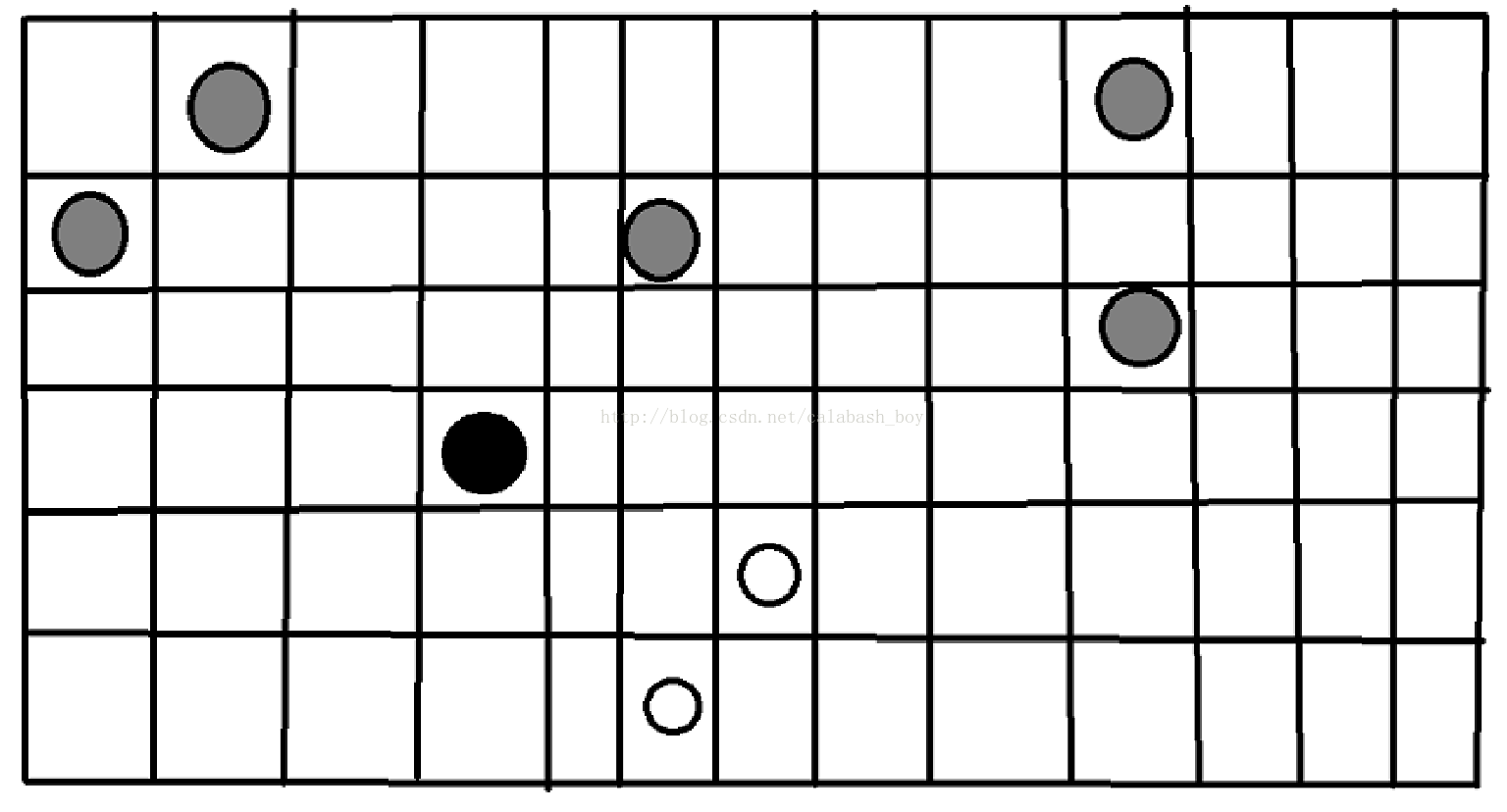
那么假设我们的图长这个样子,且灰色点是已经计数完成的点,白色点是未计数的点,黑色点是正在计数的点。
这个黑点位于(4,4)位置,我们现在要做的就是确定上下左右四个边界分别有多少种选取方式,显然白色点的序大于黑色点,黑色点的矩阵可以包含他们也可以不包含他们,因此下边界无限制,可以取到(4,5,6==n)三种方式,而由于黑点同一行的左右以及上边的行有不能包含的点,因此一个矩阵上边界对应了左右的最远边界。我们需要枚举矩阵的上边界(4,3,2,1),并且因为上边界i-1的时候上边界i要考虑的点仍然要考虑,而且要额外考虑i-1这行的灰色点。因此左右最远边界要持续进行维护。上边界是ii的时候,考虑所有ii行的灰色点,在黑点左边的去更新左边界最远点,在黑点右边的去更新有边界最远点,而刚好在黑点上边的话,说明这一行不可能作为上边界了。这个时候就结束计算黑点名下的子矩形。开始计算下一个白点。
优化:我们看第10列第1行和第3行的两个同列的灰色点,显然在上边界为3的时候,靠下的这个灰色点决定了右边界最远端,而上边界继续向上移动,右边界只可能更小,因此靠上的这个灰色点其实什么作用也没有。因此同一列只有最下边一个点有用。这样让我们在计算黑点的时候,最多只考虑之前出现的m个点,而不是理论最坏im个点,这个优化还是很关键的。因此当我们枚举(i,j)名下的矩形,上边界是xi行的时候,右边界最远是ry,左边界最远是ly,那么组合一下就得到了(n-i+1)(j-ly+1)(ry-j+1)个贡献(下边界方案左边界方案右边界方案,上边界已经确定是xi)。上边讲的一个跳出条件仍然有效。
整个算法复杂度严格小于 mn(n/2+m)(点数平摊上边界枚举数量&最多需要考虑的点),实际上跑起来是快的飞起,因为中间会跳出,而且要考虑的点没那么多。
代码:
#include<bits/stdc++.h>
using namespace std;
const int MAX = 105;
int m,n;
int mp[MAX][MAX];
int bottom[MAX];
vector< pair <int,int> > Color[MAX*MAX];///用于存储每个颜色对应的坐标点
vector<int> yIndex[MAX];///每个颜色已经遍历过的点的行号
long long calc(int col)
{
memset(bottom,0,sizeof(bottom));
memset(yIndex,0,sizeof(yIndex));
long long ans = 0;
///遍历所有的这个颜色的点
for (vector<pair <int,int> > :: iterator it=Color[col].begin(); it!=Color[col].end(); it++)
{
int ni = it->first,nj = it->second;///获取横、纵坐标
for (int i = 1; i<=m; i++)///在每一列里面找,看有没有这个颜色的点
{
if (bottom[i])
yIndex[bottom[i]].push_back(i);///把对应的列放入到行号数组里
}
int yl=1,yr=m;
bool br = false;
for (int ii = ni; ii>=1; ii--)
{
///在每一行里面找有没有这个颜色的点
for (vector<int>::iterator it = yIndex[ii].begin(); it!=yIndex[ii].end(); it++)
{
int yy = *it;
if (yy<nj)
yl = max(yl,yy+1);///寻找左边界
else if (yy>nj)
yr = min (yr,yy-1);///右边界
else
{
br = true;
break;
}
}
if (br) break;
ans+=(n-ni+1)*(nj-yl+1)*(yr-nj+1);
}
bottom[nj] = ni;
}
return ans;
}
void solve()
{
long long ans = 0;
for (int i = 0; i<=n*m; i++)
{
if (!Color[i].empty())
{
ans +=calc(i);
}
}
double anss = ((double)(4*ans))/(n*(n+1)*m*(m+1));
printf("%.9lf
",anss);
}
int main()
{
int Cas;
scanf("%d",&Cas);
while (Cas--)
{
memset(Color,0,sizeof(Color));
scanf("%d%d",&n,&m);
for (int i=1; i<=n; i++)
{
for (int j = 1; j<=m; j++)
{
scanf("%d",&mp[i][j]);
Color[mp[i][j]].push_back(make_pair(i,j));
}
}
for (int i=0; i<=n*m; i++)
{
if (!Color[i].empty())
{
sort(Color[i].begin(),Color[i].end());
}
}
solve();
}
return 0;
}