01背包入门 dp

题目引入：

有n个重量和价值分别为Wi，Vi的物品。从这些物品中挑选出总重量不超过W的物品，求所有挑选方案中的价值总和的最大值。

分析：

首先，我们用最普通的方法，针对每个物品是否放入背包进行搜索。

#include<iostream>
#include<stdio.h>
using namespace std;
int n,W;
int w[100],v[100];
///从第i个物品开始挑选总重量小于j的部分
int res(int i,int j)///i表示第i件物品，j表示的是当前背包的剩余容量
{
    int ans;
    if(i==n)///已经没有剩余物品了
        ans=0;
    else  if(j<w[i])///当前的背包容量不够放第i件物品
    {
        ans=res(i+1,j);///直接看第i+1件物品
    }
    else
    {
        ///看一下到底是第i件物品放还是不放获得的价值大
        ans=max(res(i+1,j),res(i+1,j-w[i])+v[i]);
    }
    return ans;
}
int main()
{
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&W);
    printf("%d
",res(0,W));
    return 0;
}

对于这个方法，可以明显的看出来他的搜索深度为n，对于n=4,Wi和Vi分别为{(2,3),(1,2),(3,4),(2,2)}切W为5的情况下，我们看一下res函数的递归执行过程。

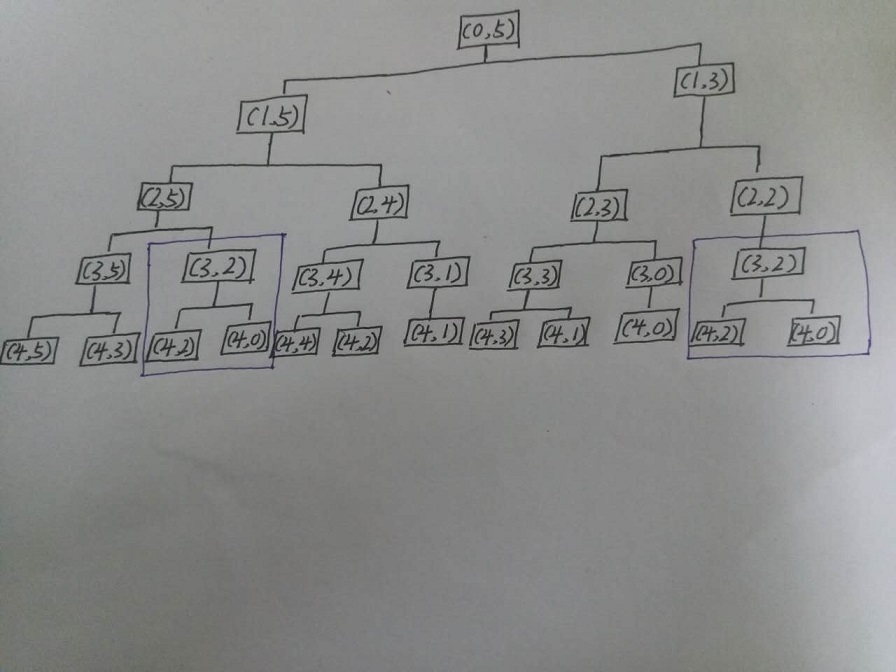
从图中我们可以看出res以(3，2)为参数调用了两次，因此我们可以把第一次的计算结果保存下来，就可以在下次直接调用。

#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
int n,W;
int w[100],v[100];
int dp[100][100];
///从第i个物品开始挑选总重量小于j的部分
int res(int i,int j)///i表示第i件物品，j表示的是当前背包的剩余容量
{
    if(dp[i][j]>0)
        return dp[i][j];
    int ans;
    if(i==n)///已经没有剩余物品了
        ans=0;
    else  if(j<w[i])///当前的背包容量不够放第i件物品
    {
        ans=res(i+1,j);///直接看第i+1件物品
    }
    else
    {
        ///看一下到底是第i件物品放还是不放获得的价值大
        ans=max(res(i+1,j),res(i+1,j-w[i])+v[i]);
    }
    return dp[i][j]=ans;
}
int main()
{
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&W);
    memset(dp,-1,sizeof(dp));
    printf("%d
",res(0,W));
    return 0;
}

接下来，我们看一下记忆化数组。记dp(i)(j)为从第i个物品开始挑选总重小于j是，总价值的最大值。因此可得到递推公式：

dp[n][j]=0;
dp[i][j]=dp[i+1][j];///当j<w[i]
dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);///当j>=w[i]

因此可以不用递归函数，直接用递推公式将各项的值计算出来。

#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
int n,W;
int w[100],v[100];
int dp[100][100];
void solve()
{
    for(int i=n-1; i>=0; i--)
        for(int j=0; j<=W; j++)
        {
            if(j<w[i])
                dp[i][j]=dp[i+1][j];
            else
                dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
        }
}
int main()
{
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%d%d",&w[i],&v[i]);
    }
    scanf("%d",&W);
    memset(dp,0,sizeof(dp));
    solve();
    printf("%d
",dp[0][W]);
    return 0;
}

刚刚讲到的dp中关于i的循环是逆向进行的。如果更改递推关系式的话循环就可以正向进行。

///dp[i][j],表示从0到i这i+1个物品中选出总重量不超过j的物品时总价值的最大值
dp[0][j]=0;
dp[i+1][j]=dp[i][j];/// j<w[i]
dp[i+1][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);//其他

则上面的solve函数进行相应的修改

void solve()
{
    for(int i=0;i<n;i++)
        for(int j=0; j<=W; j++)
        {
            if(j<w[i])
                dp[i+1][j]=dp[i][j];
            else
                dp[i+1][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);
        }
}