[吴恩达机器学习笔记]15非监督学习异常检测7-8使用多元高斯分布进行异常检测

15.异常检测 Anomaly detection

觉得有用的话,欢迎一起讨论相互学习~

吴恩达老师课程原地址

参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广

15.7-8 多变量高斯分布/使用多元高斯分布进行异常检测 -Multivariate Gaussian distribution/ Anomaly Detection using the Multivariate Gaussian Distribution

示例

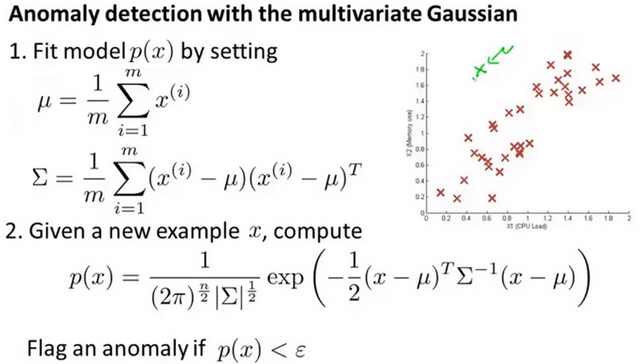
• 假设下图所示的是数据中心监测计算机是否异常的CPU加载和内存占用的特征分布，：
  
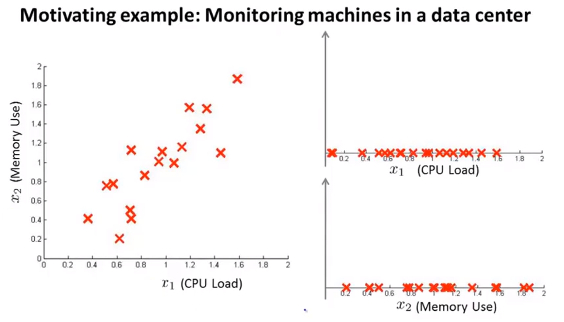
• 现使用高斯分布对特征进行拟合，计算出P(x),此时绿色的点表示 异常的样本点(CPU负载很低但是内存占用很高)，但是根据两个变量的高斯分布单独进行拟合发现其并没有错误其距离中心并不是很远，即表示考虑单变量高斯分布，其P(x_test)并不是很小， 玫红色圆圈表示使用单变量高斯分布得到P(x)的等高线图 ，所以其并不会被判定为异常数据点
  

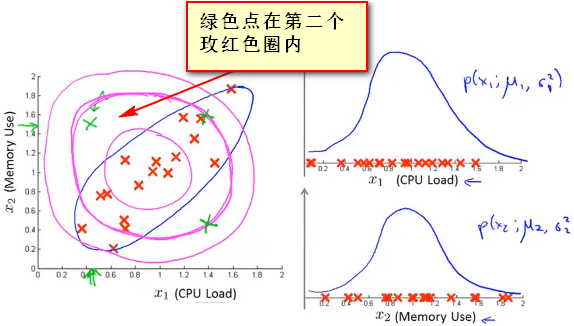
多元高斯分布

• 在一般的高斯分布模型中，我们计算 p(x)的方法是： 通过分别计算每个特征对应的几率然后将其累乘起来，在多元高斯分布模型中，我们将构建特征的协方差矩阵，用所有的特征一起来计算 p(x)。
• 一般的高斯分布模型：
  
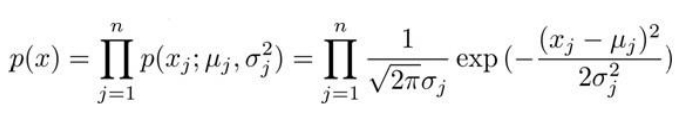
• 多元高斯分布计算步骤：
  1. 计算所有m个样本(x^{(i)})(每个样本都可以表示为一个1 * n的向量)每个特征的平均值(对应特征求平均)(mu)所以(mu)也是一个1 * n的向量，向量中的每个单元都是所有样本对应特征的平均值。
     
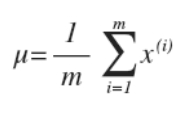
  2. 计算样本协方差矩阵，协方差矩阵计算方法请点此处
     
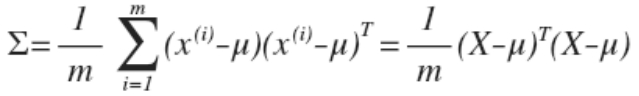
  3. 最后我们计算多元高斯分布的 p(x):
     
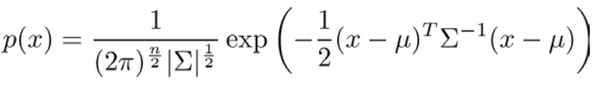
     其中，协方差矩阵使用Σ表示，使用|Σ|表示Σ矩阵的行列式，使用(Σ^{-1})表示矩阵的逆。
     

协方差矩阵对多元高斯模型的影响

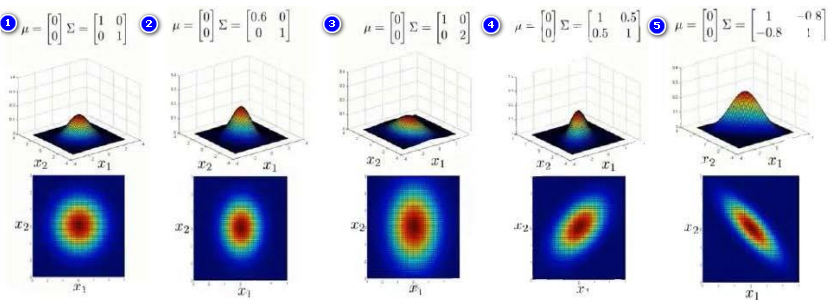
上图是 5 个不同的模型，从左往右依次分析：

1. 是一个一般的高斯分布模型
2. 通过协方差矩阵，令特征1拥有较小的偏差，同时保持特征2的偏差
3. 通过协方差矩阵，令特征2拥有较大的偏差，同时保持特征1的偏差
4. 通过协方差矩阵，在不改变两个特征的原有偏差的基础上，增加两者之间的正相关性
5. 通过协方差矩阵，在不改变两个特征的原有偏差的基础上，增加两者之间的负相关性

多元高斯分布模型与原高斯分布模型的关系

• 可以证明的是，原本的高斯分布模型是多元高斯分布模型的一个子集，即像上图中的第1、2、3，3 个例子所示，如果协方差矩阵只在对角线的单位上有非零的值时，即为原本的高斯分布模型了。

• 原高斯分布模型和多元高斯分布模型的比较

  原高斯分布模型	多元高斯分布模型
  不能捕捉特征之间的相关性但可以通过将特征进行组合的方法来解决(例如对特征进行加法或乘法)	自动捕捉特征之间的相关性
  计算代价低，能适应大规模的特征	计算代价较高 训练集较小时也同样适用(因为需要计算协方差矩阵的行列式和逆)
  	1.必须要有 m>n，否则协方差矩阵不可逆，通常需要 m>10n;2. 特征冗余(比如两个向量间线性相关，有加法或乘法的关系)也会导致协方差矩阵不可逆

原高斯分布模型被广泛使用着，如果特征之间在某种程度上存在相互关联(线性相关)的情况，可以通过构造新特征的方法来捕捉这些相关性
如果训练集不是太大，并且没有太多的特征，可以使用多元高斯分布模型