粒子群优化(PSO, particle swarm optimization)算法是计算智能领域,除了蚁群算法,鱼群算法之外的一种群体智能的优化算法,该算法最早由Kennedy和Eberhart在1995年提出的,该算法源自对鸟类捕食问题的研究。
实例分析1:
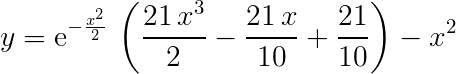
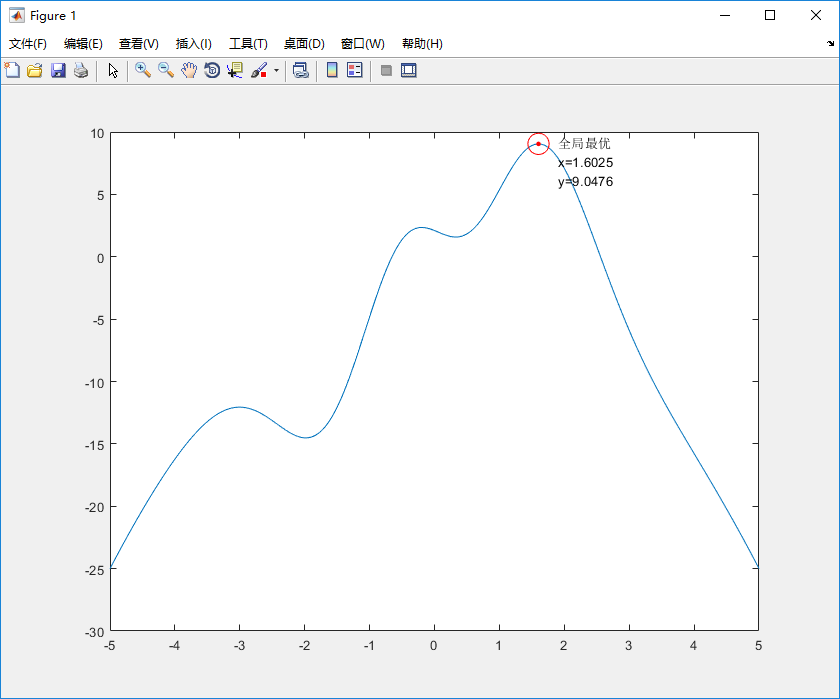
根据PSO算法思路求y最大值 ,其中x取值区间为[-5,5]
matlab代码如下:

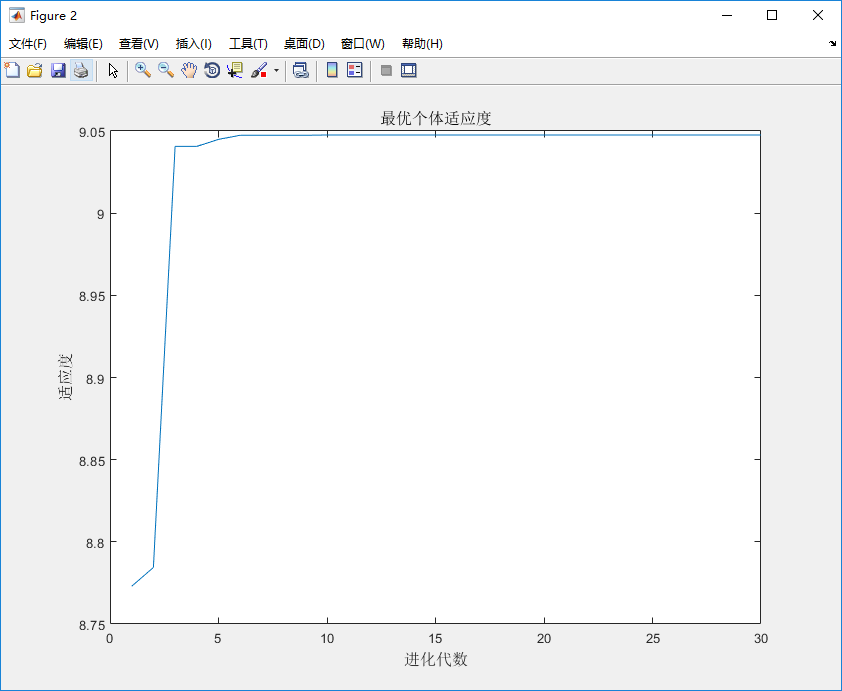
%% I. 清空环境 clc clear all %% II. 绘制目标函数曲线图 x = -5:0.01:5; y = 2.1*(1-x+5*x.^3).*exp(-x.^2/2)-x.^2; figure plot(x, y) hold on %% III. 参数初始化 这里默认惯性因子为1 c1 = 1.49445; %加速常数 取Eberhart的参考值 c2 = 1.49445; %加速常数 取Eberhart的参考值 maxgen = 30; % 进化次数 sizepop = 100; %种群规模 Vmax = 0.5; %速度步长上限 Vmin = -0.5; %速度步长下限 popmax = 5; % x的上限 popmin = -5; % x的下限 %% IV. 产生初始粒子和速度 for i = 1:sizepop % 随机产生一个种群 pop(i,:) = -10*rands(1)+5; %产生[-5,5]的初始种群 V(i,:) = 0.5 * rands(1); %初始化[-0.5,0.5]速度 % 利用fun.m子函数,计算适应度并存储到fitness(i)中 fitness(i) = fun(pop(i,:)); end %% V. 个体极值和群体极值 [bestfitness, bestindex] = max(fitness); zbest = pop(bestindex,:); %全局最佳 gbest = pop; %个体最佳 fitnessgbest = fitness; %个体最佳适应度值 fitnesszbest = bestfitness; %全局最佳适应度值 %% VI. 迭代寻优 for i = 1:maxgen for j = 1:sizepop % 速度更新 V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:)); V(j,V(j,:)>Vmax) = Vmax; V(j,V(j,:)<Vmin) = Vmin; % 种群更新 pop(j,:) = pop(j,:) + V(j,:); pop(j,pop(j,:)>popmax) = popmax; pop(j,pop(j,:)<popmin) = popmin; % 适应度值更新 fitness(j) = fun(pop(j,:)); end for j = 1:sizepop % 个体最优更新 if fitness(j) > fitnessgbest(j) gbest(j,:) = pop(j,:); fitnessgbest(j) = fitness(j); end % 群体最优更新 if fitness(j) > fitnesszbest zbest = pop(j,:); fitnesszbest = fitness(j); end end yy(i) = fitnesszbest; end %% VII. 输出结果并绘图 [fitnesszbest zbest]; plot(zbest, fitnesszbest,'r.','MarkerSize',10) plot(zbest, fitnesszbest,'ro','MarkerSize',16) x_text=['x=',num2str(zbest)]; % x横坐标转换为字符串 y_text=['y=',num2str(fitnesszbest)]; % y横坐标转换为字符串 max_text=char('全局最优',x_text,y_text); % 生成标志最大值点的字符串 text(zbest+0.3, fitnesszbest-1.4,max_text) %图上绘出全局最优的数据值 figure plot(yy) title('最优个体适应度','fontsize',12); xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

function y = fun(x) % 函数用于计算粒子适应度值 %x input 输入粒子 %y output 粒子适应度值 y = 2.1*(1-x+5*x.^3).*exp(-x.^2/2)-x.^2;
实例分析2:
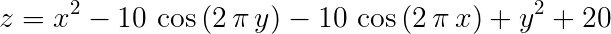
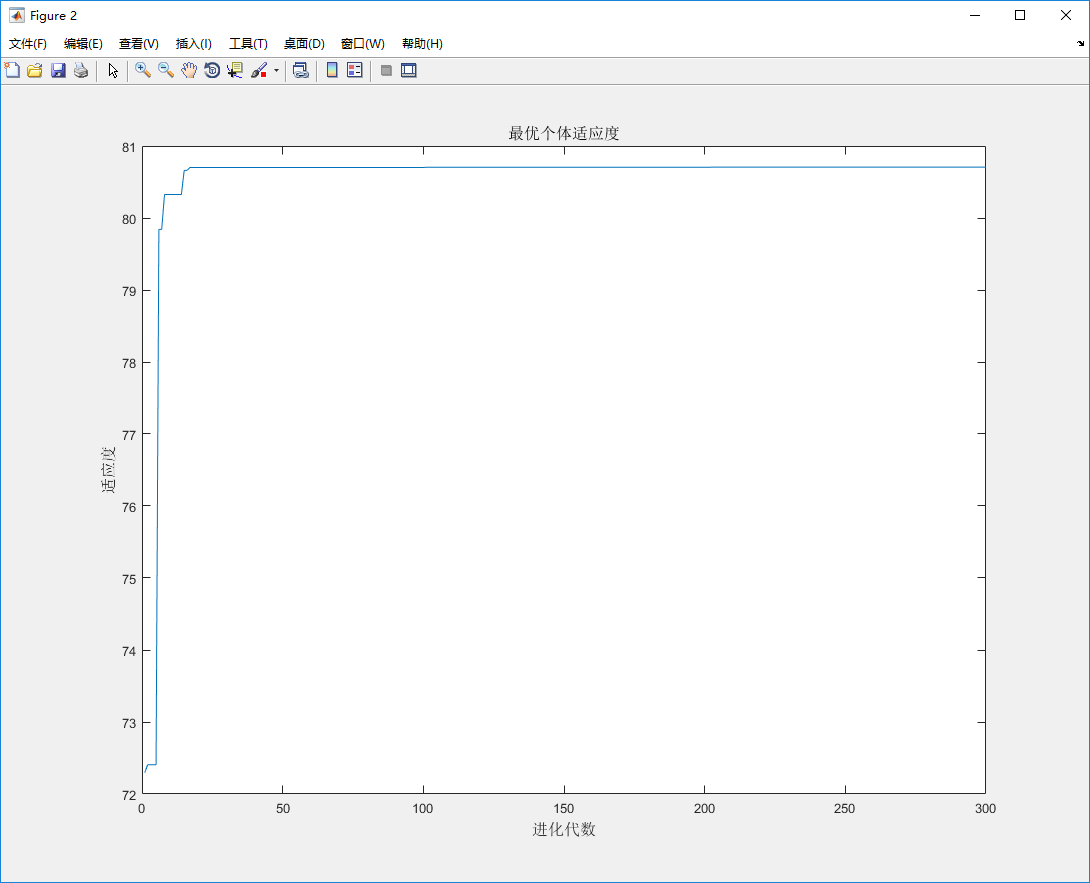
根据PSO算法思路求z最大值 ,其中x,y取值区间为[-5,5]

%% I. 清空环境 clc clear %% II. 绘制目标函数曲线 figure [x,y] = meshgrid(-5:0.01:5,-5:0.01:5); z = x.^2 + y.^2 - 10*cos(2*pi*x) - 10*cos(2*pi*y) + 20; surf(x,y,z) shading flat; %去除网格线 hold on %% III. 参数初始化 c1 = 1.49445; c2 = 1.49445; maxgen = 300; % 进化次数 sizepop = 100; %种群规模 Vmax = 1; Vmin = -1; popmax = 5; popmin = -5; %% IV. 产生初始粒子和速度 for i = 1:sizepop % 随机产生一个种群 pop(i,:) = 5*rands(1,2); %初始种群 V(i,:) = rands(1,2); %初始化速度 % 计算适应度 fitness(i) = fun(pop(i,:)); %染色体的适应度 end %% V. 个体极值和群体极值 [bestfitness bestindex] = max(fitness); zbest = pop(bestindex,:); %全局最佳 gbest = pop; %个体最佳 fitnessgbest = fitness; %个体最佳适应度值 fitnesszbest = bestfitness; %全局最佳适应度值 %% VI. 迭代寻优 for i = 1:maxgen for j = 1:sizepop w=1; %这里惯性因子w设为1,过小会导致局部最优 过大导致搜索粗糙 一般建议取0.6-0.75 % 速度更新 V(j,:) = w*V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:)); V(j,find(V(j,:)>Vmax)) = Vmax; V(j,find(V(j,:)<Vmin)) = Vmin; % 种群更新 pop(j,:) = pop(j,:) + V(j,:); pop(j,find(pop(j,:)>popmax)) = popmax; pop(j,find(pop(j,:)<popmin)) = popmin; % 适应度值更新 fitness(j) = fun(pop(j,:)); end for j = 1:sizepop % 个体最优更新 if fitness(j) > fitnessgbest(j) gbest(j,:) = pop(j,:); fitnessgbest(j) = fitness(j); end % 群体最优更新 if fitness(j) > fitnesszbest zbest = pop(j,:); fitnesszbest = fitness(j); end end yy(i) = fitnesszbest; end %% VII.输出结果 [fitnesszbest, zbest] plot3(zbest(1), zbest(2), fitnesszbest,'r.','MarkerSize',20) plot3(zbest(1), zbest(2), fitnesszbest,'ro','MarkerSize',16) x_text=['x=',num2str(zbest(1))]; % x横坐标转换为字符串 y_text=['y=',num2str(zbest(2))]; % y横坐标转换为字符串 z_text=['z=',num2str(fitnesszbest)]; %全局最优值z转换为字符串 max_text=char('全局最优',x_text,y_text,z_text); % 生成标志最大值点的字符串 text(zbest(1)+0.3,zbest(2)+0.3, fitnesszbest-1.4,max_text) %图上绘出全局最优的数据值 figure plot(yy) title('最优个体适应度','fontsize',12); xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);

function y = fun(x) %函数用于计算粒子适应度值 %y output 粒子适应度值 y = x(1).^2 + x(2).^2 - 10*cos(2*pi*x(1)) - 10*cos(2*pi*x(2)) + 20;

其中要注意的是惯性因子ω越大,粒子飞行的速度和位置更新的幅度就越大,偏离原先寻优轨道的程度也就越大,从而发现新的解域;相反,如果惯性因子ω越小,有利于局部寻优,提高搜索精度,惯性因子ω的大小决定了粒子对当前速度继承的多少.
所以实际操作中开始将惯性因子设置得较大,然后再迭代的过程中逐步减小,这样可以使得粒子群在开始优化时得到较大的解空间,后期逐渐收缩到较好的区域进行更精细化的搜索,以加快收敛与精度.
为了更好的平衡全局搜索与局部搜索,故提出线性递减惯性权重LDIW(linear decreasing inertia weight)
ω(k)=ω(start)-(ω(start)-w(end))(T(max)-k)/T(max)
其中ω(start)为初始惯性权重,一般取0.9,w(end)为迭代至最大次数时的惯性权重,一般取0.4,k为当前迭代次数,T(max)为最大迭代次数.

ws = 0.9; we = 0.4; maxgen = 300; hold on; for k = 1:maxgen w(k) = ws - (ws-we)*(k/maxgen); end plot(w,'linewidth',3); for k = 1:maxgen w(k) = ws - (ws-we)*(k/maxgen)^2; end plot(w,'r-.','linewidth',3); for k = 1:maxgen w(k) = ws - (ws-we)*(2*k/maxgen-(k/maxgen)^2); end plot(w,'k--.','linewidth',3); for k = 1:maxgen w(k) = we * (ws/we)^(1/(1+10*k/maxgen)); end plot(w,'--','linewidth',3); legend('线性惯性权重递减','常用权重2','常用权重3','常用权重4') xlabel('迭代次数') ylabel('速度更新权重W')

