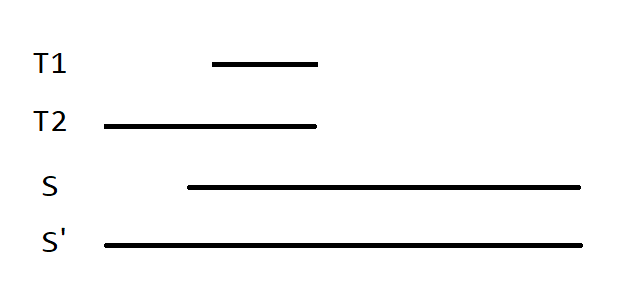【CF 700E】Cool Slogans

CF 700E。

Description

给出一个长度为 \(n\) 的字符串 \(\mathrm{str}\)。你需要构造一个尽量字符串序列 \(s_1, s_2, \cdots, s_k\)，满足：

• 对于任意 \(1 \leq i \leq n\)，\(s_i\) 为 \(\mathrm{str}\) 的子串。
• 对于任意 \(1 < i \leq n\)，\(s_{i - 1}\) 在 \(s_i\) 中至少出现了两次（可重叠）。

只需求出 \(k\) 的最大值即可。

数据范围：\(1 \leq n \leq 2 \times 10^5\)。
时空限制：\(4000 \ \mathrm{ms} / 500 \ \mathrm{MiB}\)。

Solution

引理 1

一定存在一种最优方案，使得 \(s_{i - 1}\) 为 \(s_i\) 的 border。

证明

对于一个串 \(s_i\)，将其首尾多余的部分去掉，此时 \(s_i\) 即为 \(s_{i - 1}\) 的 border。按 \(i\) 从小到大将 \(s_i\) 的多余部分去掉即可得到满足该性质的方案。

根据「引理 1」，可以得知 \(s_{i - 1}\) 为 \(s_i\) 的严格后缀。考虑将原串的 SAM 建出。

引理 2

在 SAM 的 parent 树上，对于任意一个状态 \(x\) 与其祖先状态 \(y\)，\(y\) 表示的所有子串在 \(x\) 表示的最长串的出现次数相同。

证明

反证法，考虑如图所示的子串结构。串 \(S\) 是状态 \(x\) 所表示的最长串；串 \(T_1, T_2\) 是状态 \(y\) 所表示的任意两个子串，这两个子串在 \(S\) 中的出现次数不同，必然会出现如图所示的结构。此时可以构造一个串 \(S'\) 来使得 \(T_1, T_2\) 在 \(S'\) 中的出现次数相同。

由于 \(\mathrm{endpos}(x) \subsetneqq \mathrm{endpos}(y)\)，则出现 \(S\) 的地方，前面总会跟着一个串 \(T_2\)。这样的话会使得 \(S, T_2\) 组合成一个 \(S'\)，可以推出 \(\mathrm{endpos}(S) = \mathrm{endpos}(S')\)，这与 \(S\) 为状态 \(x\) 所表示的最长串矛盾，故假设不成立。

Q.E.D

根据「引理 2」，可以得知对于 SAM 的每个状态，我们都只需要记录其所表示的最长串的等级信息即可。

此时就可以在 parent 树上 dp，设 \(f_i\) 表示从根到节点 \(i\) 的最大等级，设 \(g_i\) 表示从根到节点 \(i\) 最大等级串的状态编号。

• 若 \(x\) 所表示的最长串中出现了两次 \(g_{\mathrm{Fa}_x}\) 所表示的最长串，则

\[f_x = f_{{\mathrm{Fa}_x}} + 1 \\g_x = x \]

• 否则

\[f_x = f_{\mathrm{Fa}_x} \\g_x = g_{\mathrm{Fa}_x} \]

运用可持久化线段树合并维护 \(\mathrm{endpos}\) 集合，来判断每次是否可以成功转移。

时间复杂度 \(\mathcal{O}(n \log n)\)。

#include <cstdio>
#include <cstring>
#include <algorithm>

const int N = 200100;

int n;
char str[N];

namespace SGT {
	const int SIZE = 10001000;

	int cT;
	struct node {
		int lc, rc;
	} t[SIZE];

	void insert(int &p, int l, int r, int x) {
		p = ++ cT;
		if (l == r) return;
		int mid = (l + r) >> 1;
		if (x <= mid)
			insert(t[p].lc, l, mid, x);
		else
			insert(t[p].rc, mid + 1, r, x);
	}

	int merge(int p, int q) {
		if (!p || !q) return p ^ q;
		int x = ++ cT;
		t[x].lc = merge(t[p].lc, t[q].lc);
		t[x].rc = merge(t[p].rc, t[q].rc);
		return x;
	}

	bool ask(int p, int l, int r, int s, int e) {
		if (!p) return 0;
		if (s <= l && r <= e) return 1;
		int mid = (l + r) >> 1;
		if (s <= mid && ask(t[p].lc, l, mid, s, e)) return 1;
		if (mid < e && ask(t[p].rc, mid + 1, r, s, e)) return 1;
		return 0;
	}
}

int ans;

namespace SAM {
	const int SIZE = N * 2; 

	int cT = 1, Last = 1;
	struct node {
		int trans[26];
		int link, maxl;
	} t[SIZE];

	int root[SIZE], pos[SIZE];

	int tot, head[SIZE], ver[SIZE], Next[SIZE];
	void add_edge(int u, int v) {
		ver[++ tot] = v;    Next[tot] = head[u];    head[u] = tot;
	}

	void extend(int id, int c) {
		int p = Last,
			np = Last = ++ cT;

		SGT::insert(root[np], 1, n, id);
		pos[np] = id;

		t[np].maxl = t[p].maxl + 1;

		for (; p && t[p].trans[c] == 0; p = t[p].link) t[p].trans[c] = np;

		if (!p) {
			t[np].link = 1;
		} else {
			int q = t[p].trans[c];

			if (t[q].maxl == t[p].maxl + 1) {
				t[np].link = q;
			} else {
				int nq = ++ cT;

				t[nq] = t[q], t[nq].maxl = t[p].maxl + 1, pos[nq] = pos[q];
                                t[np].link = t[q].link = nq;
				for (; p && t[p].trans[c] == q; p = t[p].link) t[p].trans[c] = nq;
			}
		}
	}

	void build_tree() {
		for (int i = 2; i <= cT; i ++)
			add_edge(t[i].link, i);
	}

	void dfs(int u) {
		for (int i = head[u]; i; i = Next[i]) {
			int v = ver[i];
			dfs(v);
			root[u] = SGT::merge(root[u], root[v]);
		}
	}

	int f[SIZE], g[SIZE];

	void dp(int u) {
		if (t[u].link == 1) {
			f[u] = 1, g[u] = u;
		} else if (u > 1) {
			int pa = t[u].link;
			if (SGT::ask(root[g[pa]], 1, n, pos[u] - t[u].maxl + t[g[pa]].maxl, pos[u] - 1)) {
				f[u] = f[pa] + 1, g[u] = u;
			} else {
				f[u] = f[pa], g[u] = g[pa];
			}
		}

		ans = std::max(ans, f[u]);

		for (int i = head[u]; i; i = Next[i]) {
			int v = ver[i];
			dp(v);
		}
	}
}

int main() {
	scanf("%d", &n);
	scanf("%s", str + 1);

	for (int i = 1; i <= n; i ++)
		SAM::extend(i, str[i] - 'a');

	SAM::build_tree();
	SAM::dfs(1);
	SAM::dp(1);

	printf("%d\n", ans);

	return 0;
}