目录
一、思维导图
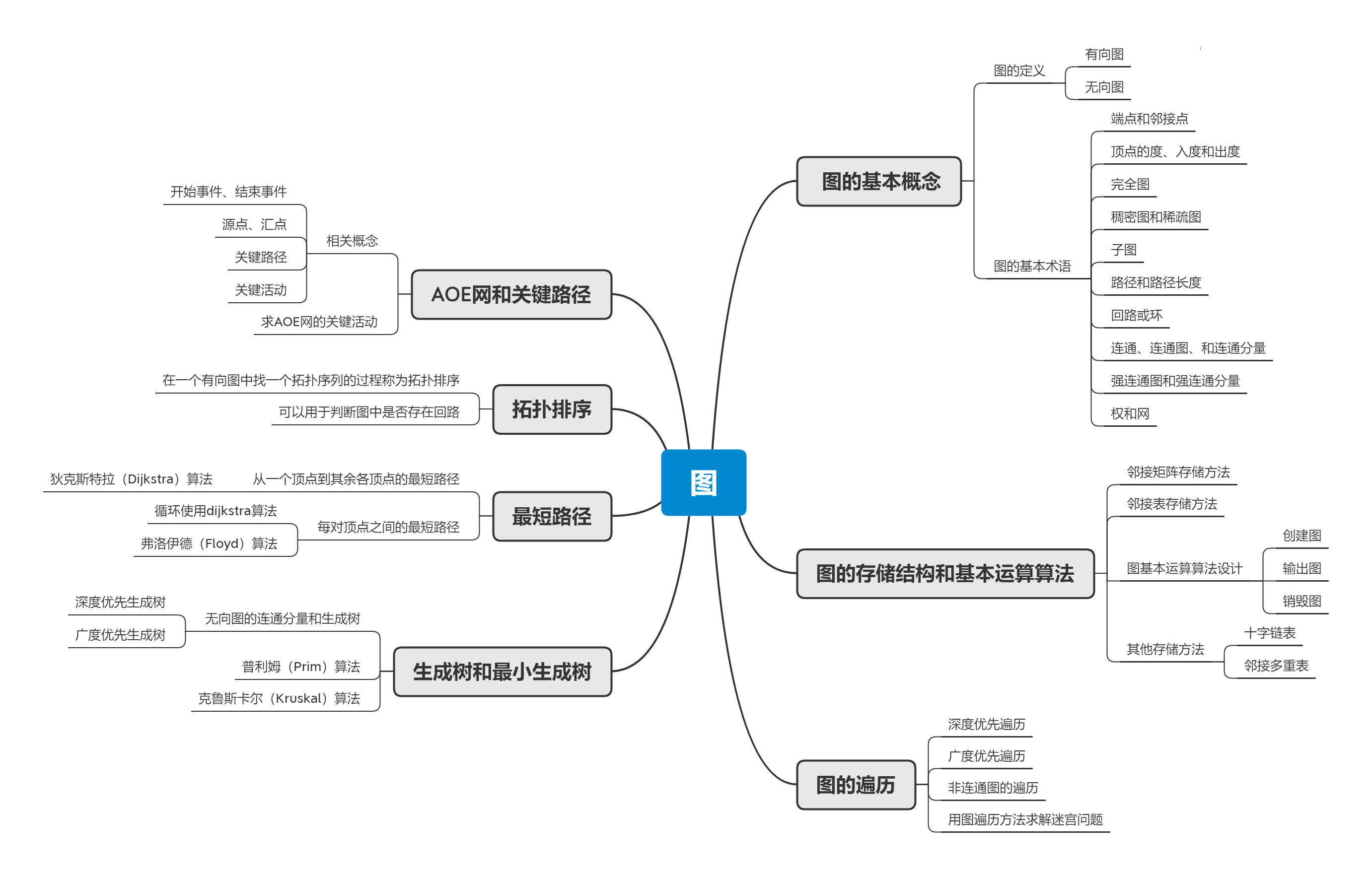
二、重要概念的笔记
图的邻接矩阵的相关算法设计
邻接矩阵存储结构及创建图
#include<iostream>
#include<string>
#include<queue>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
#define MAXVEXNUM 1000
#define MAXV 20
#define INF 0x7fffffff
typedef int ArcCell;
typedef int VexType;
typedef struct {
VexType vexs[MAXVEXNUM];//点的集合
ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
int vexNum, arcNum;
}MyGraph;
int visited[100];
int flag = 0;
int LocateVex(MyGraph*& G, VexType value)
{
for (int i = 0; i < G->vexNum; i++)
{
if (value == G->vexs[i])
return i;
}
return -1;
}
void CreateAdj2(MyGraph*& G, int n, int e) {
G = new MyGraph;
G->vexNum = n;
G->arcNum = e;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
G->arcs[i][j] = 0;
}
}
for (int i = 1; i <= n; i++) {
G->vexs[i] = i;
}
for (int j = 1; j <= G->arcNum; j++) {
int x, y; int value;
//cout << "请输入x点、y点的值及x到y的边的值:" << endl;
cin >> x; cin >> y;
//cout << "x=" << x << " "; cout << " y=" << y << " "; cout << " value=" << value << endl;
G->arcs[x][y] = 1;
G->arcs[y][x] = 1;
}
}
邻接矩阵的DFS
void DFS(MyGraph* G, int i) {
visited[i] = 1;
printf("%c ", G->vexs[i]);
for (int j = 0; j < G->vexNum; j++) {
if (G->arcs[i][j]!=0 && !visited[j]) {
DFS(G, j);
}
}
}
void DFSTraverse(MyGraph* G) {
for (int i = 0; i < G->vexNum; i++) {
visited[i] = 0;
}
for (int i = 0; i < G->vexNum; i++) {
if (!visited[i]) {
DFS(G, i);
}
}
}
邻接矩阵的BFS
void BSTTraverse(MyGraph* G) {
queue<int>Q;
for (int i = 0; i < G->vexNum; i++) {
visited[i] = 0;
}
for (int i = 0; i < G->vexNum; i++) {
if (!visited[i]) {
visited[i] = 1;
printf("%c ", G->vexs[i]);
Q.push(i);
while (!Q.empty()) {
i = Q.front();
Q.pop();
for (int j = 0; j < G->vexNum; j++) {
if (G->arcs[i][j]!=0 && !visited[j]) {
visited[j] = 1;
printf("%c ", G->vexs[j]);
Q.push(j);
}
}
}
}
}
}
输出邻接矩阵
void printMGraph(MyGraph*& G)
{
for (int i = 0; i < G->vexNum; i++)
{
for (int j = 0; j < G->vexNum; j++)
{
cout << G->arcs[i][j] << " ";
}
cout << endl;
}
}
利用邻接矩阵判断两个顶点之间有无路径
存在路径则返回true,不存在则返回false
bool printPathBetweenVex(MyGraph*& G, char startV, char endV) {
queue<int>Q;
char a[100]; int k = 0;
for (int i = 0; i < G->vexNum; i++) {
visited[i] = 0;
}
int i = LocateVex(G, startV);
if (i == -1) {
return false;
}
for (; i < G->vexNum; i++) {
if (!visited[i]) {
visited[i] = 1;
a[k] = G->vexs[i];
k++;
//printf("%c ", G->vexs[i]);
Q.push(i);
while (!Q.empty()) {
i = Q.front();
Q.pop();
for (int j = 0; j < G->vexNum; j++) {
if (G->arcs[i][j] != 0 && !visited[j]) {
visited[j] = 1;
a[k] = G->vexs[j];
k++;
//printf("%c ", G->vexs[j]);
Q.push(j);
}
}
}
}
}
for (int i = 0; i < k; i++) {
if (a[i] == endV) {
return true;
}
}
return false;
}
图的邻接表的相关算法设计
邻接表存储结构及创建图
#define MAXV 20
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include<queue>
using namespace std;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
int visited[MAXV];
int flag = 0;
void CreateAdj1(AdjGraph*& G, int n, int e) {//无向图的创建
ArcNode* p;
G = new AdjGraph;
for (int i = 1; i <= n; i++) {
G->adjlist[i].firstarc = NULL;
}
int x, y;
for (int i = 1; i <= e; i++) {
cin >> x >> y;
p = new ArcNode;
p->adjvex = y;
p->nextarc = G->adjlist[x].firstarc;
G->adjlist[x].firstarc = p;
p = new ArcNode;
p->adjvex = x;
p->nextarc = G->adjlist[y].firstarc;
G->adjlist[y].firstarc = p;
}
G->n = n;
G->e = e;
}
邻接表的DFS
void DFS(AdjGraph* G, int v) {
for (int i = 1; i <= G->n; i++) visited[i] = 0;
ArcNode* p;
flag++;
if (flag == 1) {
printf("%d", v);
}
else {
printf(" %d", v);
}
visited[v] = 1;
p = G->adjlist[v].firstarc;
while (p != NULL) {
if (visited[p->adjvex] == 0) {
DFS(G, p->adjvex);
}
p = p->nextarc;
}
}
邻接表的BFS
void BFS(AdjGraph* G, int v) {
for (int i = 1; i <= G->n; i++) visited[i] = 0;
ArcNode* p;
int t;
queue<int>Q;
printf("%d", v);
visited[v] = 1;
Q.push(v);
while (!Q.empty()) {
t = Q.front();
Q.pop();
p = G->adjlist[t].firstarc;
while (p != NULL) {
if (visited[p->adjvex] == 0) {
printf(" %d", p->adjvex);
visited[p->adjvex] = 1;
Q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
普利姆(Prim)算法
基本思路:对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示除去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。
过程图解:
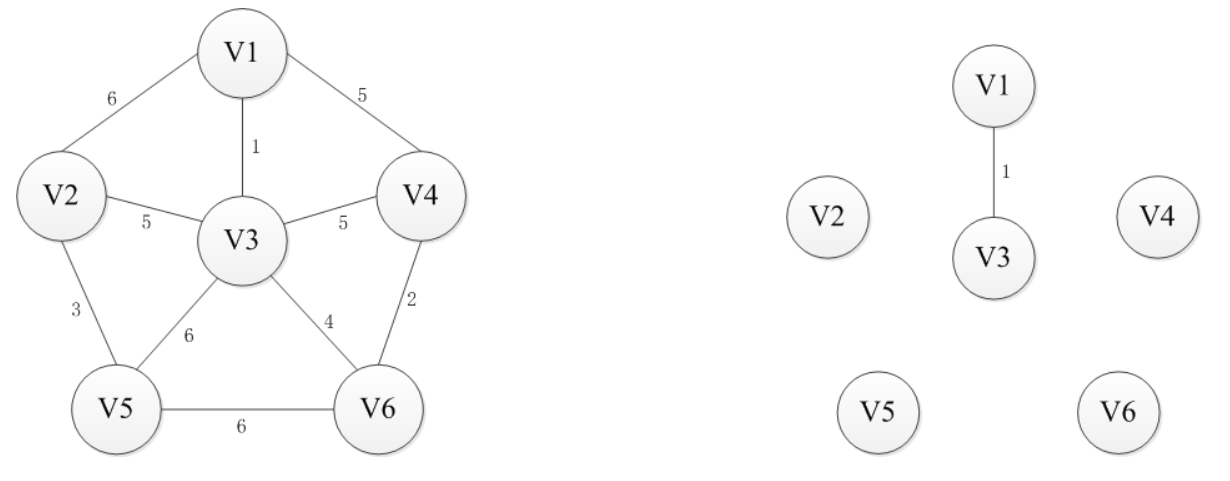

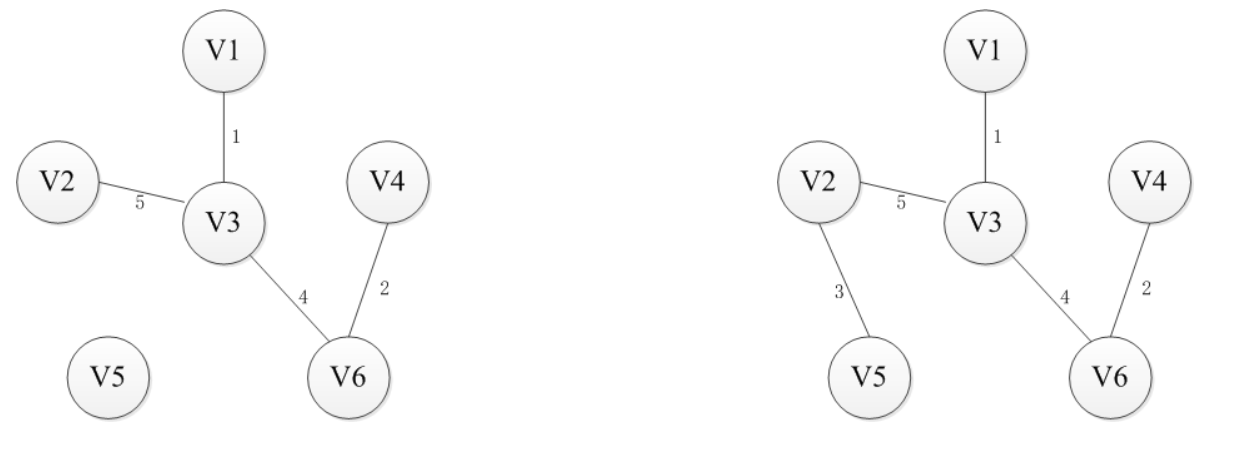
算法实现:
代码出自:https://www.cnblogs.com/yx1999/p/10357626.html
void MiniSpanTree_Prim(MGragh G)
{
int mini,i,j,k;
int adjvex[MAXVEX]; //保存相关顶点下标
int lowcost[MAXVEX]; //保存相关顶点间边的权值
lowcost[0] = 0;//这里把第0位的权值置0表示v0已加入生成树
//ps:lowcost[i] = 0 表示i那个下标的顶点加入生成树
adjvex[0] = 0; //初始化第一个顶点的下标为0
for(i = 0; i < G.numVertexes; i++)
{
lowcost[i] = G.arc[0][i];//将vo相关顶点的权值存入lowcost数组
adjvex[i] = 0;//置所有下标为v0
}
for(i = 1; i < G.numVertexes; i++) //最小生成树开始辽
{
mini = INFITINY; //先把权值的最小值置为无限大
j = 1;
k = 0;
while(j < G.numVertexes)
{
if(lowcost[j] != 0 && lowcost[j] < mini)//判断并向lowcost中添加权值
{
mini = lowcost[j];
k = j;
}
j++;
}
printf("(%d %d)",lowcost[k],k);
lowcost[k] = 0;//置0表示这个定点已经完成任务,找到最小权值分支
for(j = 1; j < G.numVertexes; j++)
{
if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
{
lowcost[j] = G.arc[k][j];
adjvex[j] = k;
}
}
}
}
克鲁斯卡尔(Kruskal)算法
基本思路:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路。 首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止。
对比普里姆和克鲁斯卡尔算法,克鲁斯卡尔算法主要针对边来展开,边数少时效率比较高,所以对于稀疏图有较大的优势;而普里姆算法对于稠密图,即边数非常多的情况下更好一些。
过程图解:
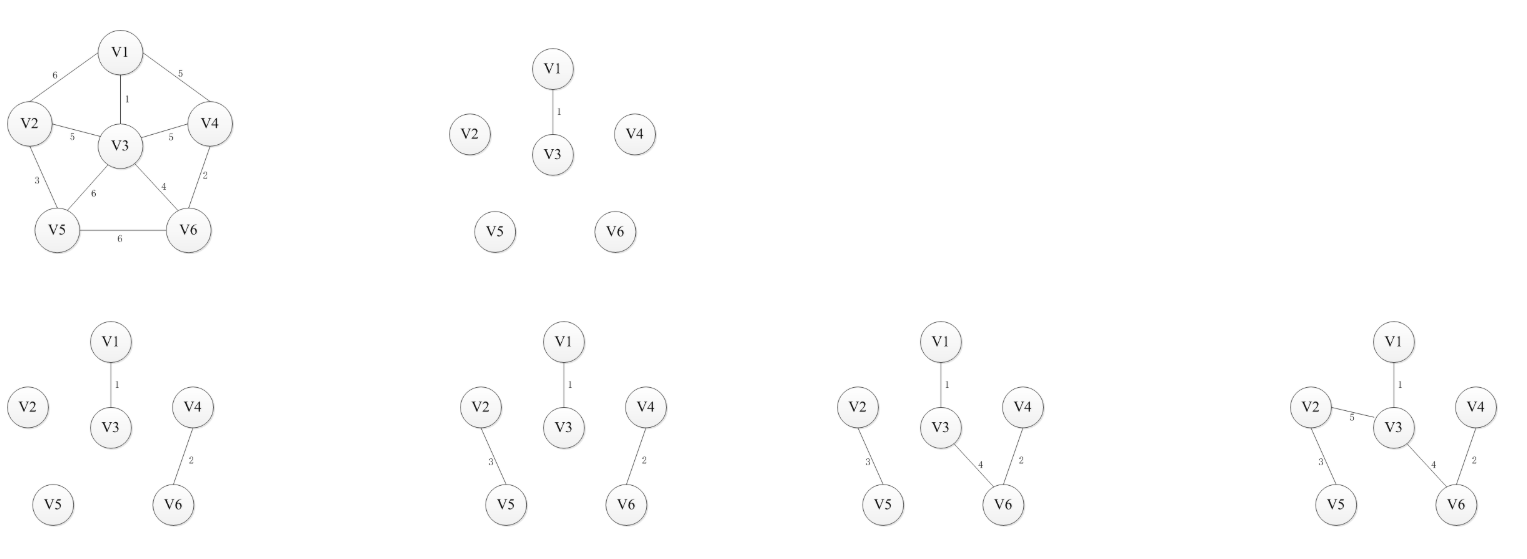
算法实现:
代码出自:https://blog.csdn.net/jnu_simba/article/details/8870481
void kruskal(Graph G)
{
int i,m,n,p1,p2;
int length;
int index = 0; // rets数组的索引
int vends[MAX]={0}; // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
EData rets[MAX]; // 结果数组,保存kruskal最小生成树的边
EData *edges; // 图对应的所有边
// 获取"图中所有的边"
edges = get_edges(G);
// 将边按照"权"的大小进行排序(从小到大)
sorted_edges(edges, G.edgnum);
for (i=0; i<G.edgnum; i++)
{
p1 = get_position(G, edges[i].start); // 获取第i条边的"起点"的序号
p2 = get_position(G, edges[i].end); // 获取第i条边的"终点"的序号
m = get_end(vends, p1); // 获取p1在"已有的最小生成树"中的终点
n = get_end(vends, p2); // 获取p2在"已有的最小生成树"中的终点
// 如果m!=n,意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
if (m != n)
{
vends[m] = n; // 设置m在"已有的最小生成树"中的终点为n
rets[index++] = edges[i]; // 保存结果
}
}
free(edges);
// 统计并打印"kruskal最小生成树"的信息
length = 0;
for (i = 0; i < index; i++)
length += rets[i].weight;
printf("Kruskal=%d: ", length);
for (i = 0; i < index; i++)
printf("(%c,%c) ", rets[i].start, rets[i].end);
printf("
");
}
狄克斯特拉(Dijkstra)算法
代码出自:https://blog.csdn.net/qq_16261421/article/details/106005266?fps=1&locationNum=2
void Dijkstra(MGraph g,int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i<g.n;i++)
{
dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v;
else
path[i]=-1;
}
s[v]=1;path[v]=0; //源点编号v放入s中
for (i=0;i<g.n;i++) //循环直到所有顶点的最短路径都求出
{
mindis=INF; //mindis置最小长度初值
for (j=0;j<g.n;j++) //选取不在s中且具有最小距离的顶点u
if (s[j]==0 && dist[j]<mindis)
{
u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入s中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF && dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
三、疑难问题及解决方案
PTA 7-4 公路村村通
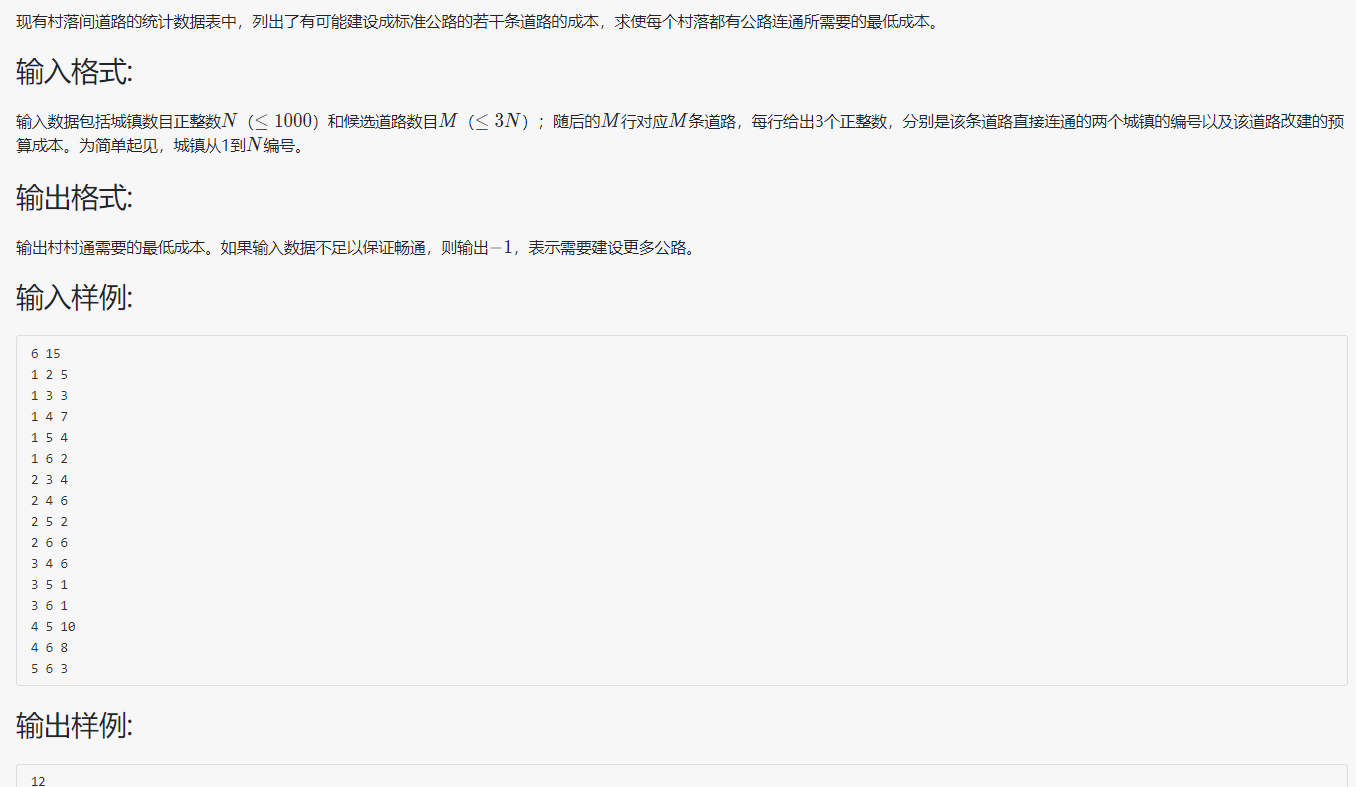
代码:
#include<iostream>
using namespace std;
#define MAXNUM 1001
#define INF 0X7fffffff
typedef struct {
int edges[MAXNUM][MAXNUM];
int vexs[MAXNUM];
int vexNum, arcNum;
}MyGraph;
int visited[MAXNUM] = { 0 };
void Prim(MyGraph* G, int v) {
int lowcast[MAXNUM];
int lowcost[MAXNUM];
int MIN;
int closet[MAXNUM], i, j, k;
for (i = 1; i <= G->vexNum; i++) {
lowcost[i] = G->edges[v][i];
closet[i] = v;
}
for (i = 1; i < G->vexNum; i++) {
MIN = INF;
for (j = 1; j <= G->vexNum; j++) {
if (lowcost[j] != 0 && lowcost[j] < MIN) {
MIN = lowcost[j];
k = j;
}
}
lowcast[i] = lowcost[k];
lowcost[k] = 0;
for (j = 1; j <= G->vexNum; j++) {
if (lowcost[j] != 0 && G->edges[k][j] < lowcost[j]) {
lowcost[j] = G->edges[k][j];
closet[j] = k;
}
}
}
int result = 0;;
for (i = 1; i < G->vexNum; i++) {
result += lowcast[i];
}
printf("%d", result);
}
void IfConnected(MyGraph* G,int v) {
visited[v] = 1;
for (int i = 1; i <= G->vexNum; i++) {
if (visited[i] == 0 && G->edges[v][i] != 0 && G->edges[v][i] != INF) {
IfConnected(G, i);
}
}
}
int main() {
int N, M;
cin >> N >> M;
MyGraph* G;
G = new MyGraph;
int i, j, x, y, value;
G->vexNum = N; G->arcNum = M;
for (i = 1; i <= N; i++) {
G->vexs[i] = i;
}
for (i = 1; i <= N; i++) {
for (j = 1; j <= N; j++) {
if (i == j) G->edges[i][j] = 0;
else G->edges[i][j] = INF;
}
}
for (i = 1; i <= M; i++) {
cin >> x >> y >> value;
G->edges[x][y] = value;
G->edges[y][x] = value;
}
if (M < N - 1) {
printf("-1");
return 0;
}
IfConnected(G, 1);
for (i = 1; i <= N; i++) {
if (visited[i] == 0) {
cout << "-1";
return 0;
}
}
Prim(G, 1);
return 0;
}
其他问题
关于本章图的算法,我们已经学了普利姆算法、克鲁斯卡尔算法、Dijkstra算法、Floyd算法、拓扑排序等等,虽然每种算法各有其对应的问题,但是有时候普利姆算法、克鲁斯卡尔算法和Dijkstra算法会弄混,做题目做着做着就搞混在一起了。