前言
一道模板题
后缀数组(SA)是一个比较强大的处理字符串的算法,是有关字符串的比较基础是吗?算法,所以必须掌握
实现主要有倍增和(DC3),而我太弱了只学了倍增
目录
知识点
1.基数排序+倍增
2.最长公共前缀Height
一些要维护的东西
(s):就是这个字符串,长度为(len)
(rank[i]):表示(i到len)这个后缀在所有后缀中的排名
(sa[i]):表示排名为(i)的后缀的首字符下标
(height[i]):表示相邻两个排名的后缀的的最长公共前缀的长度
基数排序+倍增构造SA
首先基数排序:就是低位到高位一位一位桶排,详见baidu
怎么排序?
如果一位一位来,那不就成了暴力了
所以我们要倍增排序
具体来说,对于一个长度为(2^k)的字符串,我们可以把它看成是两个长度为(2^{k-1})的字符串组成的,那么就相当于它有两个关键字,我们就从长度为(1)开始,每次对这两个关键字排序不就行了
一张古老的图
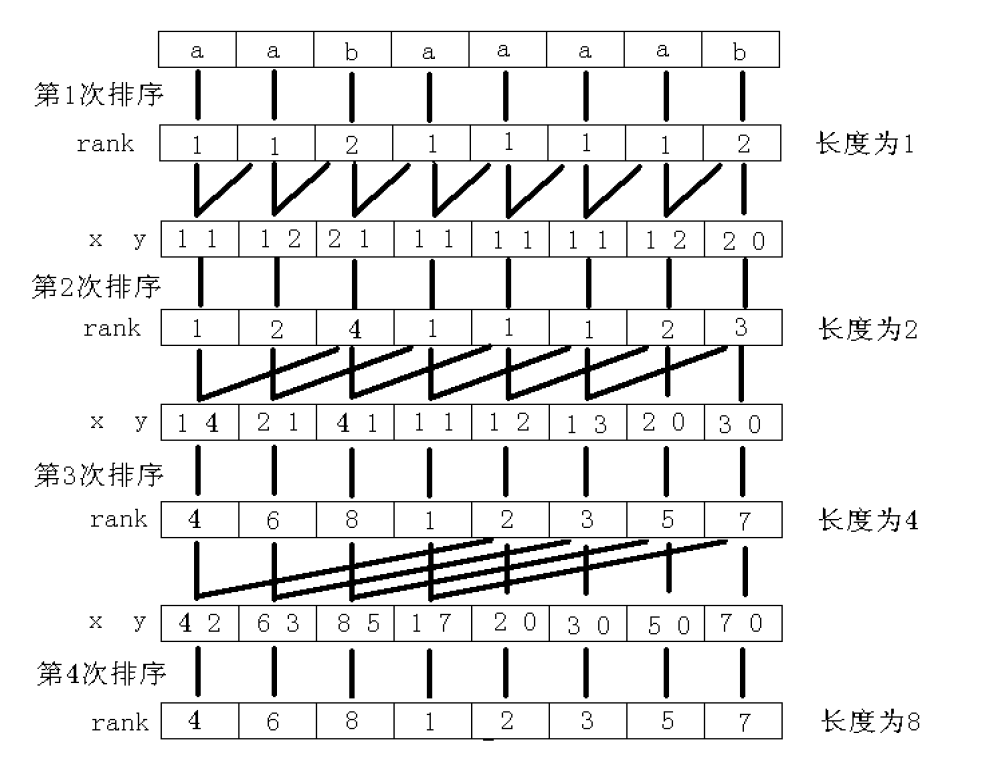
看代码
# include <bits/stdc++.h>
# define IL inline
# define RG register
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
const int _(1e6 + 5);
int len, sa[_], t[_], a[_], rk[_], y[_];
char s[_];
//t是桶;a和s一样;rk就是rank;y是辅助rk的数组,和sa性质相似;sa就是sa
IL bool Cmp(RG int i, RG int j, RG int k){ return y[i] == y[j] && y[i + k] == y[j + k]; } //确定两个子串是否相同
IL void Sort(){
RG int m = 80; //初始字符集大小
for(RG int i = 1; i <= len; ++i) ++t[rk[i] = a[i]];
for(RG int i = 1; i <= m; ++i) t[i] += t[i - 1];
for(RG int i = len; i; --i) sa[t[rk[i]]--] = i; //初始一个字符的排序
for(RG int k = 1; k <= len; k <<= 1){ //倍增
RG int l = 0;
for(RG int i = 0; i <= m; ++i) y[i] = 0;
//先按第二关键字排序,y记下编号
for(RG int i = len - k + 1; i <= len; ++i) y[++l] = i; //越界的第二关键字没有,放前面
for(RG int i = 1; i <= len; ++i) if(sa[i] > k) y[++l] = sa[i] - k; //剩下的按顺序排
//再按rk第一关键字排序
for(RG int i = 0; i <= m; ++i) t[i] = 0;
for(RG int i = 1; i <= len; ++i) ++t[rk[y[i]]];
for(RG int i = 1; i <= m; ++i) t[i] += t[i - 1];
for(RG int i = len; i; --i) sa[t[rk[y[i]]]--] = y[i];
//用这次的rk更新下次的
swap(rk, y); rk[sa[1]] = l = 1;
for(RG int i = 2; i <= len; ++i) rk[sa[i]] = Cmp(sa[i], sa[i - 1], k) ? l : ++l; //相同的rk一样
if(l >= len) break; //此时肯定不用排了,大家都不同
m = l; //记录下次排序的字符集大小
}
}
int main(RG int argc, RG char* argv[]){
scanf(" %s", s + 1); len = strlen(s + 1);
for(RG int i = 1; i <= len; ++i) a[i] = s[i] - '0';
Sort();
for(RG int i = 1; i <= len; ++i) printf("%d ", sa[i]);
return puts(""), 0;
}
有点难理解,多看几个博客就可以了
最长公共前缀---Height
有个(sa)和(rank)并没有什么卵用,这个时候就有(Height)这个美妙的东西
怎么求?
暴力求(O(n^2))显然不行
那么这个时候要利用(h)的美妙性质:(h[i]≥h[i-1]-1)
证明:设后缀(suf[k]和suf[i-1])为两个相邻排名的后缀,它们的最长公共前缀就是(h[i-1])
同时去掉第一个字符,那么就是(suf[k+1]和suf[i]),那它们两个的最长公共前缀显然就是(h[i-1]-1)
所以(suf[i])和排在它前面的后缀的最长公共前缀至少是(h[i-1]-1)
那么(h)就可以很快求出来了,那么(height)也就能很快求出来了
for(RG int i = 1; i <= len; ++i){
h[i] = max(0, h[i - 1] - 1);
if(rk[i] == 1) continue;
while(a[i + h[i]] == a[sa[rk[i] - 1] + h[i]]) ++h[i];
}
for(RG int i = 1; i <= len; ++i) height[i] = h[sa[i]];
刚刚学代码比较丑,而且可能有问题
应用
1.最长公共前缀
题:给定一个字符串,询问某两个后缀的最长公共前缀。
分析:
就是区间(height)的最小值,(RMQ)问题
重复子串:字符串A在字符串B中至少出现两次,则称A是B的重复子串。
2.可重叠最长重复子串
题:给定一个字符串,求最长重复子串,重复的两个子串可以重叠。
分析:
只需要求 height 数组里的最大值即可
3.不可重叠最长重复子串
题:给定一个字符串,求最长重复子串,重复的两个子串不能重叠。
分析:
考虑二分答案,每次二分一个答案(k),把(height)按(>=k)分组
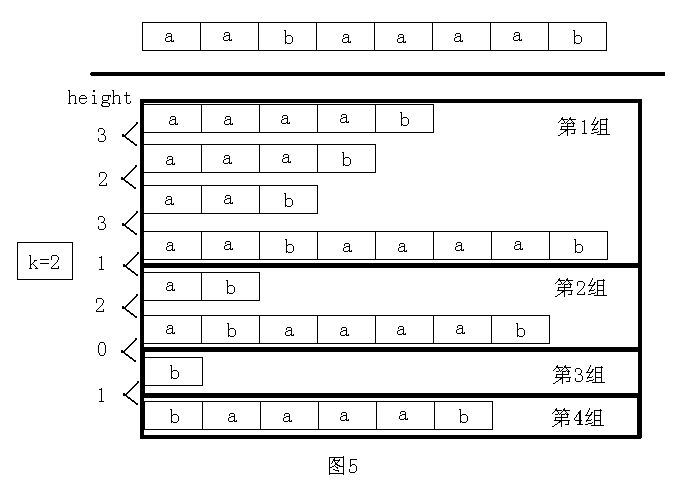
最长公共前缀不小于 k 的两个后缀一定在同一组。对于每组后缀,只须判断每个后缀的 sa 值的最大值和最小值之差是否不小于k即可
另外:利用 height 值对后缀进行分组的方法很常用
4.可重叠的 k 次最长重复子串
题:给定一个字符串,求至少出现 k 次的最长重复子串,这 k 个子串可以重叠
分析:
也是二分答案+分组,判断有没有一个组的后缀个数不小于 k
5.不相同的子串的个数
题:给定一个字符串,求不相同的子串的个数。
分析:
每个子串一定是某个后缀的前缀,也就是求所有后缀不同前缀的个数
每来一个后缀(suf(i))就会有,(len-sa[i]+1)的新的前缀,又由于有(height)个重复的,那么就是(len-sa[i]+1-height)的贡献
还有很多用法见下面的文献