CYJian的水题大赛

实在没忍住就去打比赛了然后一耗就是一天

最后Rank19还是挺好的（要不是乐多赛不然炸飞），这是唯一一套在Luogu上号称水题大赛的而实际上真的是水题大赛的比赛

好了我们开始看题

---

T1 八百标兵奔北坡

首先看到这道题你要先仔细想一想切比雪夫距离是什么

我们更加形象地理解一下就会知道这是一个等腰三角形（算了还是看图吧，对于红色的格子，所有黄色的格子对于它都在北面）：

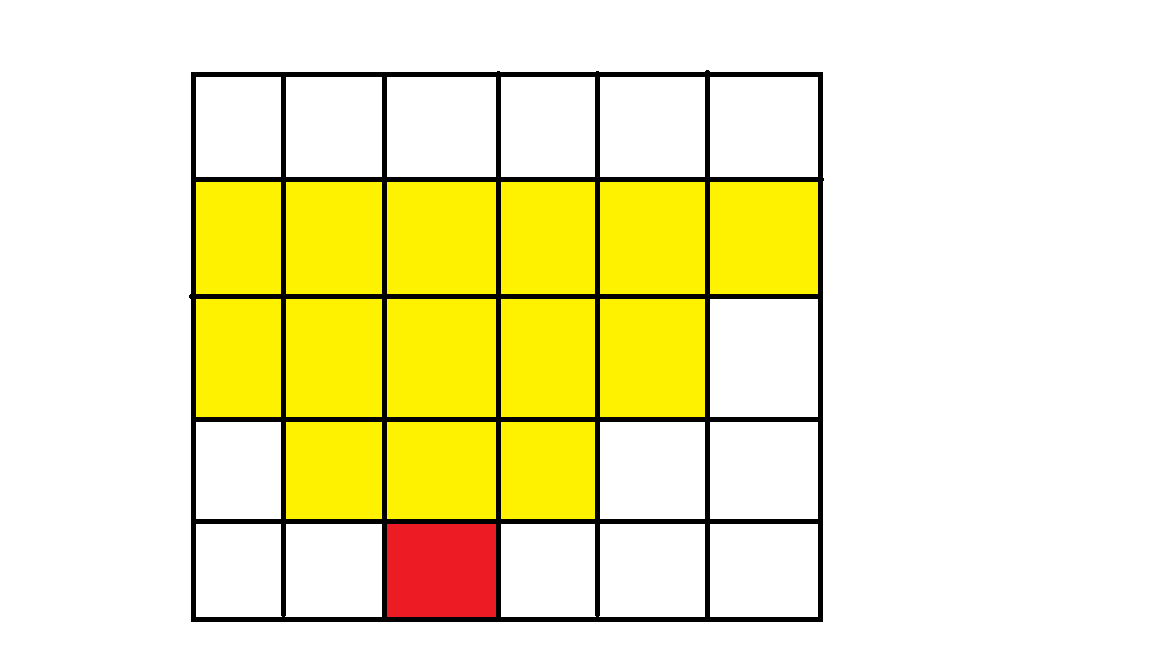
然后仔细看一下就发现每一个点可以设计一个DP的思想（类似于过河卒）：

• (f_{i,j}=0(if (i,j) is a mountain.))
• (f_{i,j}=min(min(f_{i-1,j-1},f_{i-1,j}),f_{i-1,j+1})+1)

CODE

#include<cstdio>
#include<cctype>
#include<cstring>
using namespace std;
const int N=1e3+5,fx[4]={0,1,0,-1},fy[4]={1,0,-1,0};
int n,m,k,h[N][N],x,y,f[N][N];
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch; while (!isdigit(ch=tc()));
    while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void write(int x)
{
    if (x>9) write(x/10);
    putchar(x%10+'0');
}
inline bool check(int x,int y)
{
    for (register int i=0;i<4;++i)
    {
        int xx=x+fx[i],yy=y+fy[i];
        if (xx>=1&&xx<=n&&yy>=1&&yy<=m&&h[xx][yy]>=h[x][y]) return 0;
    }
    return 1;
}
inline int min(int a,int b)
{
    return a<b?a:b;
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i,j; read(n); read(m); read(k);
    for (i=1;i<=n;++i)
    for (j=1;j<=m;++j) read(h[i][j]);
    memset(f,63,sizeof(f));
    for (i=1;i<=n;++i)
    for (j=1;j<=m;++j)
    if (check(i,j)) f[i][j]=0; else f[i][j]=min(min(f[i-1][j-1],f[i-1][j]),f[i-1][j+1])+1;
    while (k--)
    {
        read(x); read(y);
        if (f[x][y]<n) write(f[x][y]),putchar('
'); else puts("Pool Babingbaboom!");
    }
    return 0;
}

当然我比赛时不是这么写的

对于每一行处理出山的前缀和，然后查询时暴力向上跳即可，期望复杂度为(O(klogn))，最坏复杂度为(O(kn))

CODE

// luogu-judger-enable-o2
#include<cstdio>
#include<cctype>
#include<cstring>
using namespace std;
const int N=1005,K=100005,fx[4]={0,1,0,-1},fy[4]={1,0,-1,0};
int h[N][N],l[N][N],n,m,k,INF,x,y;
bool vis[N][N];
inline char tc(void)
{
    static char fl[100000],*A=fl,*B=fl;
    return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
    x=0; char ch; while (!isdigit(ch=tc()));
    while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void write(int x)
{
    if (x>9) write(x/10);
    putchar(x%10+'0');
}
inline bool check(int x,int y)
{
    for (register int i=0;i<4;++i)
    {
        int xx=x+fx[i],yy=y+fy[i];
        if (xx>=1&&xx<=n&&yy>=1&&yy<=m&&h[xx][yy]>h[x][y]) return 0;
    }
    return 1;
}
inline int max(int a,int b)
{
    return a>b?a:b;
}
inline int min(int a,int b)
{
    return a<b?a:b;
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i,j; read(n); read(m); read(k);
    for (i=1;i<=n;++i)
    for (j=1;j<=m;++j)
    read(h[i][j]);
    for (i=1;i<=n;++i)
    for (j=1;j<=m;++j)
    l[i][j]=l[i][j-1]+check(i,j);
    while (k--)
    {
        read(x); read(y); bool flag=0;
        for (i=x;i>=1;--i)
        if ((l[i][y]-l[i][max(y-x+i-1,0)])||(l[i][min(y+x-i,m)]-l[i][y-1])) { write(x-i); putchar('
'); flag=1; break; }
        if (!flag) puts("Pool Babingbaboom!");
    }
    return 0;
}

---

T2 灰化肥，会挥发

这应该是一道状压板子题了（主要是做的时候状态不是很好莫名很烦，然后都没有想用String来存最优解，一算数组炸了就去写暴力了）

我们考虑状压，设(f_{i,j})表示以第(i)（为了方便以([0,n))编号）个仓库结尾且状态为(j)（为二进制下的01串）的最优解

然后对于两点间的距离我们大力BFS预处理即可（存到(dis_{i,j})中）

然后稍加推到即可得出状态转移方程：

(f_{i,joplus(1<<i)}=f_{k,j}+dis_{k.i})

其中(oplus)表示异或，感觉这种转移实在是太基础了。

关于字典序的问题转移的时候直接一起搞即可（String在比较字典序是实在好用）

CODE

// luogu-judger-enable-o2
#include<cstdio>
#include<iostream>
#include<cctype>
#include<algorithm>
#include<cstring>
#include<string>
using namespace std;
const int R=505,N=18,state=66000,fx[4]={0,1,-1,0},fy[4]={1,0,0,-1};
char a[R][R],ch;
int r,c,x[N],y[N],n,dis[R][R],q[R*R][2],step[R][R],tot,f[N][state],num,INF,MIN;
bool vis[R][R];
string g[N][state];
inline void BFS(int id,int x,int y)
{
    register int i,H=0,T=1; q[1][0]=x; q[1][1]=y; step[x][y]=0; vis[x][y]=1;
    while (H<T)
    {
        int xx=q[++H][0],yy=q[H][1];
        if (isalpha(a[xx][yy])) dis[id][a[xx][yy]-'A']=step[xx][yy];
        for (i=0;i<4;++i)
        {
            int xxx=xx+fx[i],yyy=yy+fy[i];
            if (xxx>0&&xxx<=r&&yyy>0&&yyy<=c&&a[xxx][yyy]!='*'&&!vis[xxx][yyy]) 
            step[xxx][yyy]=step[xx][yy]+1,q[++T][0]=xxx,q[T][1]=yyy,vis[xxx][yyy]=1;
        }
    }
}
int main()
{
    register int i,j,k; cin>>r>>c>>n; 
    for (i=1;i<=r;++i)
    for (j=1;j<=c;++j)
    {
        cin>>a[i][j];
        if (isalpha(a[i][j])) x[a[i][j]-'A']=i,y[a[i][j]-'A']=j;
    }
    memset(dis,63,sizeof(dis)); memset(f,63,sizeof(f));
    for (i=0;i<n;++i)
    memset(vis,0,sizeof(vis)),BFS(i,x[i],y[i]);
    tot=(1<<n)-1; f[0][1]=0; INF=f[0][0]; g[0][1]="A";
    for (j=1;j<=tot;++j)
    for (i=1;i<n;++i)
    {
        if (j&(1<<i)) continue;
        for (k=0;k<n;++k)
        if (k^i&&(j&(1<<k)))
        {
            if (f[k][j]==INF) continue;
            if (f[i][j^(1<<i)]>f[k][j]+dis[k][i]) f[i][j^(1<<i)]=f[k][j]+dis[k][i],ch=i+'A',g[i][j^(1<<i)]=g[k][j],g[i][j^(1<<i)]+=ch;
            if (f[i][j^(1<<i)]==f[k][j]+dis[k][i]&&g[i][j^(1<<i)]>g[k][j]) ch=i+'A',g[i][j^(1<<i)]=g[k][j],g[i][j^(1<<i)]+=ch;
        }
    }
    for (MIN=INF,i=1;i<n;++i)
    {
        if (f[i][tot]<MIN) MIN=f[i][tot],num=i;
        if (f[i][tot]==MIN&&g[i][tot]<g[num][tot]) num=i;
    }
    printf("%d
",MIN); cout<<g[num][tot]; return 0;
}

---

T3 红鲤鱼与绿鲤鱼

一道很神奇的数学题，%%%yekehe大佬5min切掉此题。

我们首先发现罚时的位置和最后一次AC都是要计算上去的，因此我们先加上去即可。

然后对答案有影响的只有那B条绿鲤鱼

然后我们固定第一个AC的位置，然后后面只有(A+B-1)个位置要填上(B-1)个AC

那还等什么，组合数大法好，接下来因为每一位对答案的贡献都是一样的，因此我们直接乘上去即可。

然后别忘了这是期望，还有除以总方案数(C_{A+B}^B)

然后我就开始暴力计算了，对于多个阶乘和逆元都一起做。

然后正常人这么写都GG了（常数太大）

然后我就第一个不服了，之后开始了我一下午的卡常工作（都ZZ地没有再接下去想一步）

最后卡时间A了！（然后就被尊称为常数之王了）

一下总结几点卡常技巧：

1. 快速幂里可以展开多做几次，这样可以减少while语句的出现次数
2. 使用循环展开大法，推荐展开10次兼顾编译速度和运行速度
3. unsigned long long比long long快将近1倍
4. 手开O2，语音选C++11（这个很重要，编译优化快到死）

卡常CODE

// luogu-judger-enable-o2
#pragma G++ optimize (2)
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
const ull mod=998244853,less=998244851;
ull n,m;
inline ull quick_pow(ull x,ull p)
{
    ull tot=1;
    while (p)
    {
        if (p&1) tot=1LL*tot*x%mod;
        x=1LL*x*x%mod; p>>=1;
        if (p&1) tot=1LL*tot*x%mod;
        x=1LL*x*x%mod; p>>=1;
        if (p&1) tot=1LL*tot*x%mod;
        x=1LL*x*x%mod; p>>=1;
    }
    return tot;
}
int main()
{
    register ull i; scanf("%lld %lld",&n,&m); n%=mod; static ull ans=1,t=1;
    for (i=1;i+9<m;i+=10) 
    {
        t=t*quick_pow(i,less)%mod; t=t*quick_pow(i+1,less)%mod;
        t=t*quick_pow(i+2,less)%mod; t=t*quick_pow(i+3,less)%mod;
        t=t*quick_pow(i+4,less)%mod; t=t*quick_pow(i+5,less)%mod;
        t=t*quick_pow(i+6,less)%mod; t=t*quick_pow(i+7,less)%mod;
        t=t*quick_pow(i+8,less)%mod; t=t*quick_pow(i+9,less)%mod;
    }
    for (;i<m;++i) t=t*quick_pow(i,less)%mod;
    for (i=n+1;i+9<n+m;i+=10) 
    {
        t=t*i%mod; t=t*(i+1)%mod;
        t=t*(i+2)%mod; t=t*(i+3)%mod;
        t=t*(i+4)%mod; t=t*(i+5)%mod;
        t=t*(i+6)%mod; t=t*(i+7)%mod;
        t=t*(i+8)%mod; t=t*(i+9)%mod;
    }
    for (;i<n+m;++i)
    t=t*i%mod; ans=5*t%mod;
    ans=ans*(n+m+1)%mod*(n+m)%mod*quick_pow(2,less)%mod; 
    ans=ans*quick_pow(t*quick_pow(m,less)%mod*(n+m)%mod,less)%mod; 
    return printf("%lld",((10*n+5*m+5)%mod+ans)%mod),0;
}

然后如果你多想1min就可以发现上面的式子:

(frac{5(2A+B+1)+5cdot C_{B+A−1}^{B-1}cdot (A+B+1)cdot frac{(A+B)}{2}}{2})=(5cdot(2A+B+1)+5Bcdot(A+B+1))

然后直接(O(1))求即可

CODE

#pragma G++ optimize (2)
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
const ull mod=998244853;
ull n,m;
inline ull quick_pow(ull x,ull p)
{
    ull tot=1;
    while (p)
    {
        if (p&1) tot=1LL*tot*x%mod;
        x=1LL*x*x%mod; p>>=1;
    }
    return tot;
}
int main()
{
    register ull i; scanf("%lld %lld",&n,&m); n%=mod; static ull ans=1;
    ans=ans*(n+m+1)%mod*(n+m)%mod*quick_pow(2,mod-2)%mod; 
    ans=5*ans*quick_pow(n+m,mod-2)%mod*m%mod; 
    return printf("%lld",((10*n+5*m+5)%mod+ans)%mod),0;
}