一大早起来先做一道DP有助于清醒脑子
首先我们肯定考虑按(x)升序依次考虑每个点,容易发现因为题目中给的是极小值均为(0),那就意味着只要向下走就一定要碰到(x)轴
因此容易设计一个状态,(f_{i,0/1})表示当前走到(i)点,从(i-1)走到(i)的路径最后是向上还是向下
考虑如何转移,我们先来看一种情况:
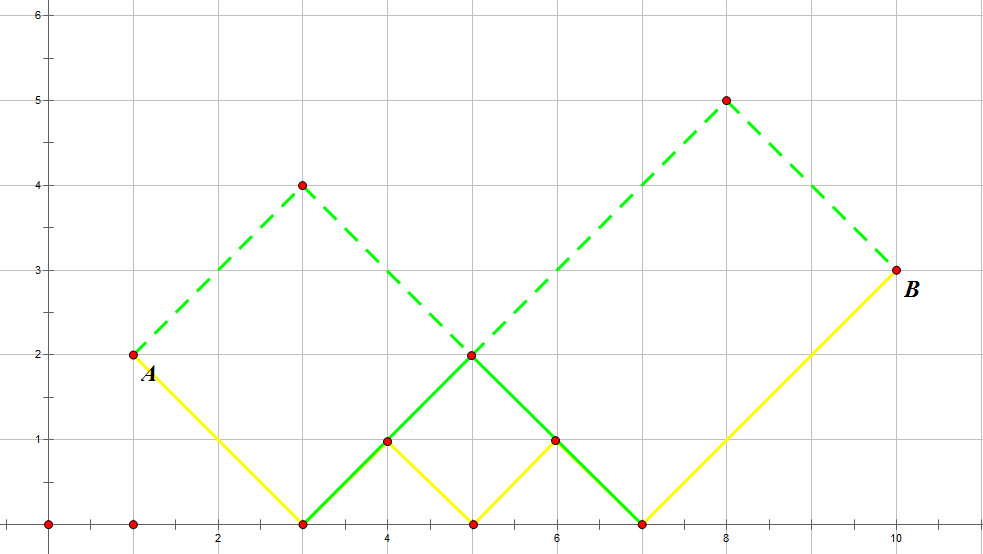
我们考虑先求出(A,B)分别向右下,左下与(x)轴的交点,首先考虑在交点之间的走法
容易发现黄色实线是一种最基本的走法,一上一下一上一下
考虑绿色实线的路径如何变化而来,其实很简单,就是在两个相邻的“锯齿”之间选择把这两个“锯齿”合并了
然后我们发现每一次合并后的图形形状都不相同且不会重复和遗漏,假设有(k)个锯齿,那么显然方案数就是(2^{k-1})
考虑加入(A,B)的情况,我们发现实线的情况和虚线的情况其实是可以相互转化的,因此系数乘上(2)即可
不过值得注意的是当(A)之前是向下走的时候,只能一口气走到底而不能走虚线路径,因此我们有转移方程:
[f_{i,0}=f_{i,1}=2^k imes f_{i-1,0}+2^{k-1} imes f_{i-1,1}
]
然后我们发现剩下的特殊情况都比较简单了,无非是两点恰好在同一直线上或是无法走到(x)轴,简单讨论即可
考虑第二问,相邻两个点如果贪心的想肯定是先向上走到最高然后向下,但是这样会被Hack掉(具体Hack数据看Luogu讨论)
被叉的原因也很简单,我们要判断两个点之间能否向上走到最高,条件允许才能转移,否则就是两点纵坐标的最大值
#include<cstdio>
#include<map>
#define RI register int
#define CI const int&
using namespace std;
const int N=1000005,mod=19940417;
int n,m,k,f[N][2],x[N],y[N],mx,tp; map <int,int> F; // f[x][0/1] 0:up/1:down
inline int quick_pow(int x,int p,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline int sum(CI x,CI y)
{
int t=x+y; return t>=mod?t-mod:t;
}
int main()
{
RI i,j; for (scanf("%d%d",&n,&k),i=1;i<=k;++i)
scanf("%d%d",&x[i],&y[i]),F[x[i]]=y[i]; F[0]=F[n]=0;
for (map <int,int>:: iterator it=F.begin();it!=F.end();++it)
x[++m]=it->first,y[m]=it->second; for (i=2;i<=m;++i)
for (f[1][1]=1,i=2;i<=m;++i)
{
bool flag=0; if (x[i]-x[i-1]==y[i]-y[i-1]) f[i][0]=sum(f[i-1][0],y[i-1]?0:f[i-1][1]); else //k=1
if (x[i]-x[i-1]==y[i-1]-y[i]) f[i][1]=sum(f[i-1][0],f[i-1][1]); else //k=-1
if (tp=x[i]-x[i-1]-y[i-1]-y[i],tp<0) f[i][1]=f[i-1][0],flag=1; else //unreached
if (!tp) f[i][0]=sum(f[i-1][0],f[i-1][1]),f[i][1]=f[i-1][0]; //one instraction
else f[i][0]=f[i][1]=sum(1LL*quick_pow(2,tp/2)*f[i-1][0]%mod,1LL*quick_pow(2,tp/2-1)*f[i-1][1]%mod),flag=1; //interval instractions
if (!y[i]) f[i][0]=0; if (flag) mx=max(mx,(x[i]-x[i-1]+y[i]+y[i-1])>>1); else mx=max(mx,max(y[i-1],y[i]));
}
return printf("%d %d",f[m][1],mx),0;
}