《大话数据结构》第9章 排序 9.8 归并排序（上）

9.8.1 归并排序介绍
        前面我们讲了堆排序，因为它用到了完全二叉树，充分利用了完全二叉树的深度是⌊log₂n⌋+1的特性，所以效率比较高。不过堆结构的设计本身是比较复杂的，老实说，能想出这样的结构就挺不容易，有没有更直接简单的办法利用完全二叉树来排序呢？当然是有。
        先来举一个例子。你们知道高考一本、二本、专科分数线是如何划分出来的吗？
        简单地说，如果各高校本科专业在某省高三理科学生中计划招收1万名，那么将全省参加高考的理科学生分数倒排序，第1万名的总分数就是当年本科生的分数线（现实可能会比这复杂，这里简化之）。也就是说，即使你是你们班级第一、甚至年级第一名，如果你没有上分数线，则说明你的成绩排不到全省前1万名，你也就基本失去了当年上本科的机会了。
        换句话说，所谓的全省排名，其实也就是每个市、每个县、每个学校、每个班级的排名合并后再排名得到的。注意我这里用到了合并一词。
我们要比较两个学生的成绩高低是很容易的，比如甲比乙分数低，丙比丁分数低。那么我们也就可以很容易得到甲乙丙丁合并后的成绩排名，同样的，戊己庚辛的排名也容易得到，由于他们两组分别有序了，把他们八个学生成绩合并有序也是很容易做到的了，继续下去……最终完成全省学生的成绩排名，此时高考状元也就诞生了。
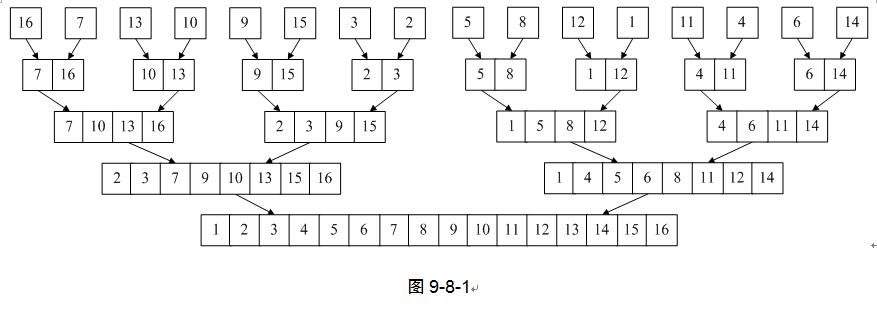
        为了更清晰地说清楚这里的思想，大家来看图9-8-1，我们将本是无序的数组序列{16,7,13,10,9,15,3,2,5,8,12,1,11,4,6,14}，通过两两合并排序后，再合并，最终获得了一个有序的数组。注意仔细观察它的形状，你会发现，它像极了一棵倒置的完全二叉树，通常涉及到完全二叉树结构的排序算法，效率一般都不低的——这就是我们要讲的归并排序法。
 

9.8.2 归并排序算法
        “归并”一词的中文含义就是合并、并入的意思，而在数据结构中的定义是将两个或两个以上的有序表组合成一个新的有序表。
        归并排序（Merging Sort）就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到⌈n/2⌉（⌈x⌉表示不小于x的最小整数）个长度为2或1的有序子序列；再两两归并，……，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法称为2路归并排序。 
        好了，有了对归并排序的初步认识后，我们来看代码。

/* 对顺序表L作归并排序 */

void MergeSort(SqList *L)

{ 

  MSort(L->r,L->r,1,L->length);

}

        一句代码，别奇怪，它只是调用了另一个函数而已。为了与前面的排序算法统一，我们用了同样的参数定义SqList *L，由于我们要讲解的归并排序实现需要用到递归调用 ，因此我们外封装了一个函数。假设现在要对数组{50,10,90,30,70,40,80,60,20}进行排序，L.length=9，我现来看看MSort的实现。

/* 将SR[s..t]归并排序为TR1[s..t] */

1 void MSort(int SR[],int TR1[],int s, int t)

2 {

3  int m;

4  int TR2[MAXSIZE+1];

5  if(s==t)

6   TR1[s]=SR[s];

7  else

8  {

9   m=(s+t)/2;   /* 将SR[s..t]平分为SR[s..m]和SR[m+1..t] */

10   MSort(SR,TR2,s,m); /* 递归地将SR[s..m]归并为有序的TR2[s..m] */

11   MSort(SR,TR2,m+1,t); /* 递归地将SR[m+1..t]归并为有序TR2[m+1..t] */

12   Merge(TR2,TR1,s,m,t); /* 将TR2[s..m]和TR2[m+1..t]归并到TR1[s..t] */

13  }

14 }

1) MSort被调用时，SR与TR1都是{50,10,90,30,70,40,80,60,20}，s=1，t=9，最终我们的目的就是要将TR1中的数组排好顺序。
2) 第5行，显然s不等于t，执行第8～13行语句块。
3) 第9行，m=(1+9)/2=5。m就是序列的正中间下标
4) 此时第10行，调用“MSort(SR,TR2,1,5);”的目标就是将数组SR中的第1～5的关键字归并到有序的TR2（调用前TR2为空数组），第11行，调用“MSort(SR,TR2,6,9);”的目标就是将数组SR中的第6～9的关键字归并到有序的TR2。也就是说，在调用这两句代码之前，代码已经准备将数组分成了两组了。如图9-8-2。
 

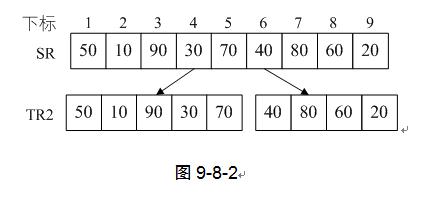
5) 第12行，函数Merge的代码细节一会再讲，调用“Merge(TR2,TR1,1,5,9);”的目标其实就是将第10和11行代码获得的数组TR2（注意它是下标为1～5和6～9的关键字分别有序）归并为TR1，此时相当于整个排序就已经完成了。如图9-8-3。
 

6) 再来看第10行递归调用进去后，s=1，t=5，m=(1+5)/2=3。此时相当于将5个记录再为三个和两个。继续递归进去，直到细分为一个记录填入TR2，此时s与t相等，递归返回，如图9-8-4的左图。每次递归返回后都会执行当前递归函数的第12行，将TR2归并到TR1中。如图9-8-4的右图。最终使得当前序列有序。
 

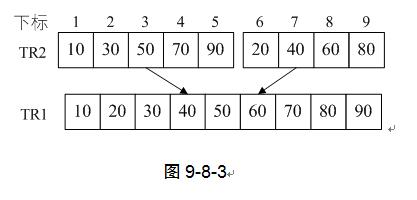
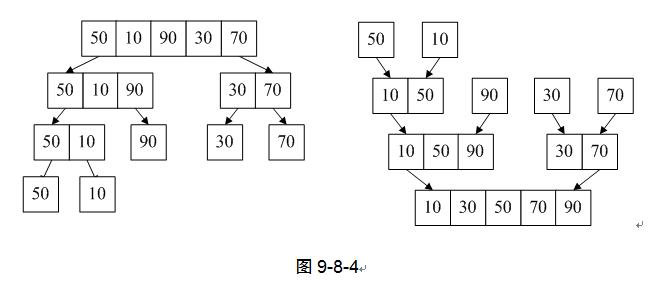
7) 同样的第11行也是类似方式，如图9-8-5。
 

8) 此时也就是刚才所讲的最后一次执行第12行代码，将{10,30,50,70,90}与{20,40,60,80}归并为最终有序的序列。
可以说，如果对递归函数的运行方式理解比较透的话，MSort函数还是很好理解的。我们来看看整个数据变换示意图，如图9-8-6。
 

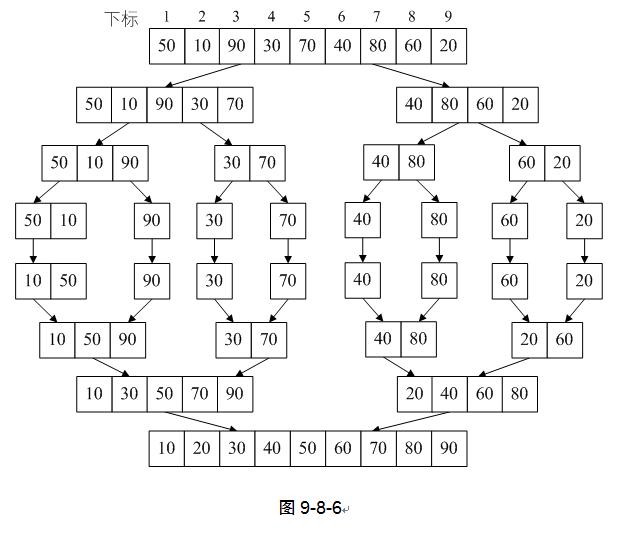
现在我们来看看Merge函数的代码是如何实现的。

/* 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n] */

1 void Merge(int SR[],int TR[],int i,int m,int n)

2 {

3  int j,k,l;

4  for(j=m+1,k=i;i<=m && j<=n;k++) /* 将SR中记录由小到大归并入TR */

5  {

6   if (SR[i]<SR[j])

7    TR[k]=SR[i++];

8   else

9    TR[k]=SR[j++];

10  }

11  if(i<=m)

12  {

13   for(l=0;l<=m-i;l++)

14    TR[k+l]=SR[i+l];  /* 将剩余的SR[i..m]复制到TR */

15  }

16  if(j<=n)

17  {

18   for(l=0;l<=n-j;l++)

19    TR[k+l]=SR[j+l];  /* 将剩余的SR[j..n]复制到TR */

20  }

21 }

1) 假设我们此时调用的Merge就是将{10,30,50,70,90}与{20,40,60,80}归并为最终有序的序列，因此数组SR为{10,30,50,70,90,20,40,60,80}，i=1，m=5，n=9。
2) 第4行，for循环，j由m+1=6开始到9，i由1开始到5，k由1开始每次加1，k值用于目标数组TR的下标。
3) 第6行，SR[i]=SR[1]=10，SR[j]= SR[6]=20，SR[i]<SR[j]，执行第7行，TR[k]=TR[1]=10，并且i++。如图9-8-7。
 

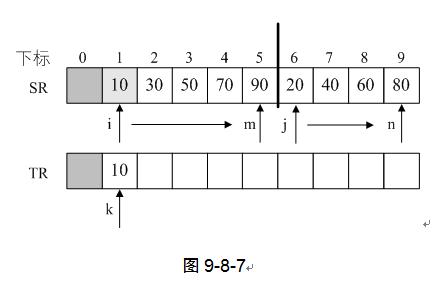
4) 再次循环，k++得到k=2，SR[i]=SR[2]=30，SR[j]= SR[6]=20，SR[i]>SR[j]，执行第9行，TR[k]=TR[2]=20，并且j++，如图9-8-8。
 

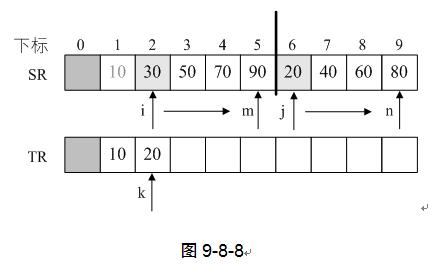
5) 再次循环，k++得到k=3，SR[i]=SR[2]=30，SR[j]= SR[7]=40，SR[i]<SR[j]，执行第7行，TR[k]=TR[3]=30，并且i++，如图9-8-9。
 

6) 接下来完全相同的操作，一直到j++后，j=10，大于9退出循环。如图9-8-10。
 

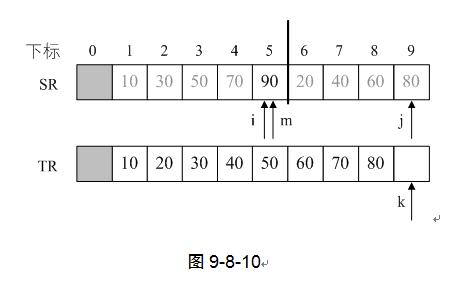
7) 第11～20行的代码，其实就将归并剩下的数组数据，移动到TR的后面。当前k=9，i=m=5，执行第13～20行代码，for循环l=0，TR[k+l]=SR[i+l]=90。大功告成。
        就这样，我们的归并排序就算是完成了一次排序工作，怎么样，和堆排序比，是不是要简单一些呢？