9.6.3 希尔排序算法
好了,为了能够真正弄明白希尔排序的算法,我们还是老办法——模拟计算机在执行算法时的步骤还研究算法到底是如何进行排序的。
希尔排序算法代码如下。
2 {
3 int i,j;
4 int increment=L->length;
5 do
6 {
7 increment=increment/3+1; /* 增量序列 */
8 for(i=increment+1;i<=L->length;i++)
9 {
10 if (L->r[i]<L->r[i-increment]) /* 需将L->r[i]插入有序增量子表 */
11 {
12 L->r[0]=L->r[i]; /* 暂存在L->r[0] */
13 for(j=i-increment;j>0 && L->r[0]<L->r[j];j-=increment)
14 L->r[j+increment]=L->r[j]; /* 记录后移,查找插入位置 */
15 L->r[j+increment]=L->r[0]; /* 插入 */
16 }
17 }
18 }
19 while(increment>1);
20 }
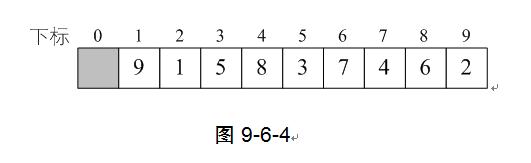
1) 程序开始运行,此时我们传入的SqList参数的值为length=9,r[10]={0,9,1,5,8,3,7,4,6,2}。这就是我们需要等待排序的序列,如图9-6-4所示。
2) 第4行,变量increment就是那个“增量”,我们初始值让它等于待排序的记录数。
3) 第5~19行是一个do循环,它提终止条件是increment不大于1时。其实也就是增量为1时就停止循环了。
4) 第7行,这一句很关键,但也是难以理解的地方,我们后面还要谈到它,先放一放。这里执行完成后,increment=9/3+1=4。
5) 第8~17行是一for循环,i从4+1=5开始到9结束。
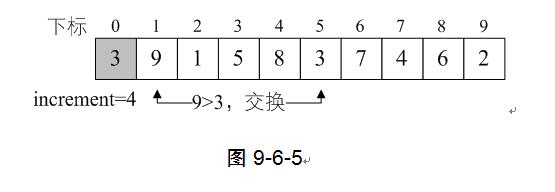
6) 第10行,判断L.r[i]与L.r[i-increment]大小,L.r[5]=3<L.r[i-increment]=L.r[1]=9,满足条件,第12行,将L.r[5]=3暂存入L.r[0]。第13~14行的循环只是为了将L.r[1]=9的值赋给L.r[5],由于循环的增量是j-=increment,其实它就循环了一次,此时j=-3。第15行,再将L.r[0]=3赋值给L.r[j+increment]=L.r[-3+4]=L.r[1]=3。如图9-6-5,事实上,这一段代码就干了一件事,就是将第5位的3和第1位的9交换了位置。
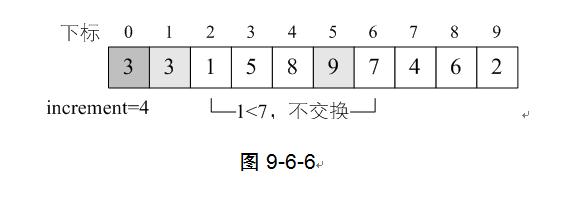
7) 循环继续,i=6,L.r[6]=7>L.r[i-increment]=L.r[2]=1,因此不交换两者数据。如图9-6-6。
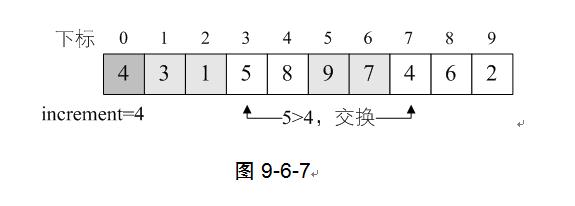
8) 循环继续,i=7,L.r[7]=4<L.r[i-increment]=L.r[3]=5,交换两者数据。如图9-6-7。
9) 循环继续,i=8,L.r[8]=6<L.r[i-increment]=L.r[4]=8,交换两者数据。如图9-6-8。
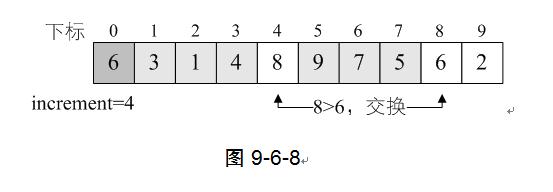
10) 循环继续,i=9,L.r[9]=2<L.r[i-increment]=L.r[5]=9,交换两者数据。注意,第13~14行是循环,此时还要继续比较L.r[5]与L.r[1]的大小,因为2<3,所以还要交换L.r[5]与L.r[1]的数据,如图9-6-9。
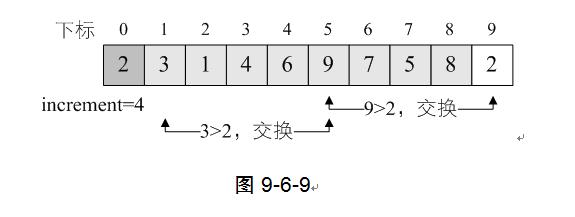
最终第一轮循环后,数组的排序结果为图9-6-10所示。细心的同学会发现,我们的数字1、2等小数字已经在前两位,而8、9等大数字已经在后两位,也就是说,通过这样的排序,我们已经让整个序列基本有序了。这其实就是希尔排序的精华所在,它将关键字较小的记录,不是一步一步地往前挪动,而是跳跃式地往前移,从而使得每次完成一轮循环后,整个序列就朝着有序坚实地迈进一步。
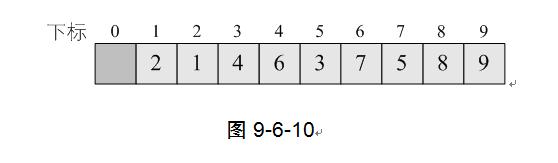
11) 我们继续,在完成一轮do循环后,此时由于increment=4>1因此我们需要继续do循环。第7行得到increment=4/3+1=2。第8~17行for循环,i从2+1=3开始到9结束。当i=3、4时,不用交换,当i=5时,需要交换数据,如图9-6-11
12) 此后,i=6、7、8、9均不用交换。如图9-6-12
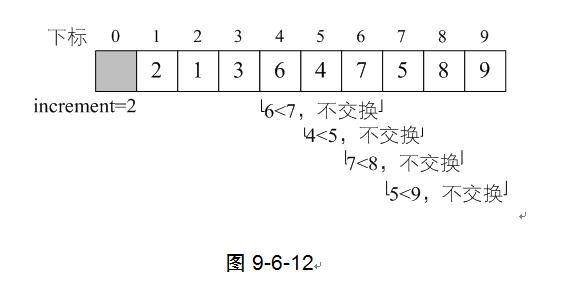
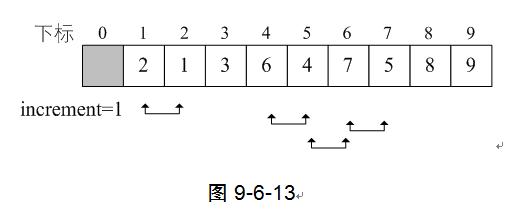
13) 再次完成一轮do循环,increment=2>1,再次do循环,第7行得到increment=2/3+1=1。此时这就是最后一轮do循环了。尽管第8~17行for循环,i从1+1=2开始到9结束,但由于当前序列已经基本有序,可交换数据的情况大为减少,效率其实很高。如图9-6-13,图中箭头连线为需要交换的关键字。
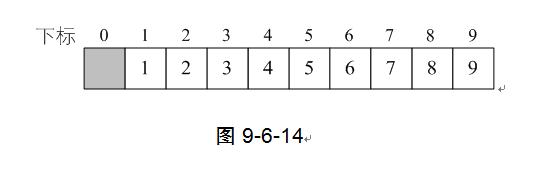
最终完成排序过程,如图9-6-14。
9.6.4 希尔排序复杂度分析
通过这段代码的剖析,相信大家有些明白,希尔排序的关键并不是随便的分组后各自排序,而是将相隔某个“增量”的记录组成一个子序列,实现跳跃式的移动,使得排序的效率提高。
这里“增量”的选取就非常关键了。我们在代码中第7行,是用increment=increment/3+1;的方式选取增量的,可究竟应该选取什么样的增量才是最好,目前还是一个数学难题,迄今为止还没有人找到一种最好的增量序列。不过大量的研究表明,当增量序列为dlta[k]=2t-k+1-1(0≤k≤t≤⌊log2(n+1)⌋)时,可以获得不错的效率,其时间复杂度为O(n3/2),要好于直接排序的O(n2)。需要注意的是,增量序列的最后一个增量值必须等于1才行。另外由于记录是跳跃式的移动,希尔排序并不是一种稳定的排序算法。
不管怎么说,希尔排序算法的发明,使得我们终于突破了慢速排序的时代(超越了时间复杂度为O(n2)),之后,相应的更为高效的排序算法也就相继出现了。