红黑树的特点
(1)每个节点都是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。【这里的叶子节点指的是空(NIL/NULL)的叶子节点】
(4)如果一个节点是红色的,则它的子节点一定是黑色的。
(5)从一个节点到这个节点的子孙节点的所有的路径上有相同数目的黑色节点。
注意:
(01) 特性(3)中的叶子节点,是只为空(NIL或null)的节点。
(02) 特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
红黑树的应用
主要用来存储有序的数据,它的时间复杂度是O(lgN),效率非常之高。如java中的TreeMap, TreeSet,C++ STL中的set map 以及
linux的虚拟内存管理,都是通过红黑树来实现的。
红黑树的基本操作(一)左旋和右旋
红黑树的基本操作中添加和删除。在对红黑树进行添加和删除后,都会用到旋转的方法,因为添加和删除会让树的结构发生变化,可能不再满足红黑树的
性质。通过旋转,我们可以使它又成为一个红黑树。
基本定义
见代码中的RBNode
旋转总结
(1)左旋和右旋是相对的两个概念,原理类似。
(2)下面是如何区分左旋和右旋。
区分左旋与右旋
仔细观察上面"左旋"和"右旋"的示意图。我们能清晰的发现,它们是对称的。无论是左旋还是右旋,被旋转的树,在旋转前是二叉查找树,并且旋转之后仍然是一颗二叉查找树。
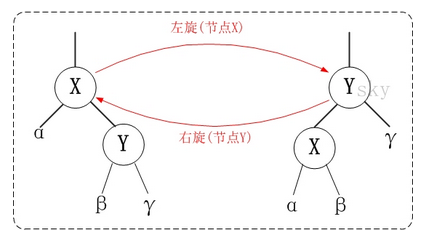
左旋示例图(以x 为节点)
z
x /
/ --(左旋)--> x
y z /
y
对x 进行左旋,意味着将x 的右孩子 设为x 的父亲节点,也就是,将x 变成了一个左节点(x成了为z的左孩子)。因此,左旋转中的左,意味着被旋转的节点将变成一个左节点。
右旋示例图
y
x
/ --(右旋)--> x
y z
z
对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为y的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。