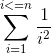TonyFang+Sps+我=5/12
滚了个大粗
2016年9月21日16:42:36 10题完工辣
01
题意:求形同的数中大于n的最小值
题解:预处理所有的(5194个),在这里面二分
#include<map> #include<stack> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline #include<set> il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() ll p[10000],_p; set<ll>q; int main(){ q.insert(1); int cnt=0; while(!q.empty()){ p[++_p]=*q.begin(); q.erase(p[_p]); ll t=p[_p]; if(t>1000000000){break;} if(2*t<=1000000000)q.insert(2*t); if(3*t<=1000000000)q.insert(5*t); if(5*t<=1000000000)q.insert(3*t); if(7*t<=1000000000)q.insert(7*t); } int T=gi; while(T--){ int n=gi; int pos = lower_bound(p+1, p+_p+1, n) - p; printf("%I64d ", p[pos]); } }
02
题解:显然收敛,如果n很大就输出一个定值,否则暴力
OrzFang
# include <stdio.h> # include <string.h> using namespace std; typedef long double ld; typedef double db; ld p[1000010]; char str[100010]; int main() { for (int i=1; i<=1000000; ++i) p[i] = p[i-1] + 1.0f/((ld)i * i); while(~scanf("%s", str)) { int sz = strlen(str), n; if(sz >= 7) puts("1.64493"); else { n = 0; for (int i=0; i<sz; ++i) n = (n<<3) + (n<<1) + str[i] - '0'; printf("%.5lf ", (db)p[n]); } } return 0; }
03
题意:给定屏蔽词集合和文章,输出屏蔽后的结果
题解:AC自动机。卡空间*****
04
题意:
有两个茶杯和一个很大的水壶,水壶可以往茶杯里倒水,没了-----zzq
题解:
很明显模拟之后我们发现要分类讨论。
①1<R≤2:倒1体积水到一个杯子即可,故答案为1
②0<R≤1:明显不用倒水即可,故答案为0
③0<L≤1:第一杯1体积,之后每次2体积往上交替加即可。答案为(R−1)/2+1
④R−L≤2,第一次倒(L+1)/2第二次倒(L+3)/2+1即可,答案为2.
⑤其他情况,在保证L的情况下,每次2体积往上交替即可。第一次倒(L+1)/2,第二次倒(L+3)/2即可,故答案为(R−L)/2+1
复杂度O(T)-----TonyFang
#include<map> #include<stack> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() #define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout); int main(){ ll l,r; while(scanf("%I64d %I64d",&l,&r)==2){ if(r<=1)puts("0"); else if(r<=2)puts("1"); else if(r-l<=2)puts("2"); else if(l<=1){ printf("%I64d ",(r-1)/2+1); }else printf("%I64d ",(r-l)/2+1); } }
05
题意:扩展石头剪刀步的出售方式,n种出手,问游戏是否平衡
题解:判断奇偶性,奇数可以,偶数不行。
06
题意:最大化欧拉路上点权异或和
题解:如果是欧拉回路,枚举起点.否则欧拉路是唯一的,判断一下度数就可以了
OrzFang
# include <stdio.h> using namespace std; int T, n, m, fa[100010], cnts[100010], deg[100010], v[100010]; inline int getf(int x) { return fa[x] == x ? x : fa[x] = getf(fa[x]); } int main() { scanf("%d", &T); while(T--) { scanf("%d%d", &n, &m); for (int i=1; i<=n; ++i) { fa[i] = i; deg[i] = 0; scanf("%d", &v[i]); } for (int i=1, u, vs; i<=m; ++i) { scanf("%d%d", &u, &vs); deg[u] ++, deg[vs] ++; int fu = getf(u), fv = getf(vs); if(fu != fv) fa[fu] = fv; } int cnt=0; bool all = 1; for (int i=1; i<=n; ++i) if(deg[i] & 1) cnt++, all = 0; if(cnt > 2) { puts("Impossible"); continue; } cnt = 0; for (int i=1; i<=n; ++i) cnts[getf(i)] ++; for (int i=1; i<=n; ++i) if(cnts[i] > 0) ++cnt; if(cnt > 1) { puts("Impossible"); continue; } if(! all) { int ans = 0; for (int i=1; i<=n; ++i) { if (deg[i]&1) deg[i] = deg[i]/2 + 1; else deg[i] /= 2; if (deg[i]&1) ans ^= v[i]; } printf("%d ", ans); } else { int ans = 0, anss, maxx=0; for (int i=1; i<=n; ++i) { deg[i] /= 2; if (deg[i]&1) ans ^= v[i]; } for (int i=1; i<=n; ++i) { anss = ans ^ v[i]; if(anss > maxx) maxx = anss; } printf("%d ", maxx); } } return 0; }
07
题意:合并x个数列的时间是长度和,合并后长度为长度和
求一个最小的k,使得合并所有数列的时间<=T
题解:
k叉哈夫曼树。
多组数据的Tnlog^2n做法卡一卡可以强行冲过去
但是根据某种合并的单调性,可以不用pq,用两个队取出前?个最小值就是Tnlogn的
#include<map> #include<stack> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() #define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout); int n,m,a[100005]; bool check(int k){ int j,ans=0,now,cnt; queue<int>p,q; for(int i=1;i<=n;i++)p.push(a[i]); if((j=(n-1)%(k-1))!=0){ now=0; for(int i=1;i<=j+1;i++) now+=p.front(),p.pop(); ans+=now; q.push(now); } while(p.size()+q.size()>1){ cnt=now=0; while(cnt<k){ if(!p.empty()&&(q.empty()||p.front()<=q.front())) now+=p.front(),p.pop(); if(!q.empty()&&(p.empty()||q.front()<=p.front())) now+=q.front(),q.pop(); cnt++; } ans+=now; q.push(now); } return ans<=m; } int main(){ int t=gi; while(t--){ n=gi;m=gi; for(int i=1;i<=n;i++)a[i]=gi; sort(a+1,a+n+1); int l=2,r=n,ans; while(l<=r){ int mid=(l+r)/2; if(check(mid)) ans=mid,r=mid-1; else l=mid+1; } printf("%d ",ans); } return 0; }
08
09
题意:有边权的树,求删除各条边后直径的和
题解:树形dp
找出树的一条直径
(a, b),然后分别以a, b为根,dp 预处理子树v的直径。
如果删掉的边不在直径上,那么有一颗子树的直径就是原树的直径,另一边已经预处理好了。如果在直径上,很显然两遍都预处理了。
#include<map> #include<stack> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() #define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout); using namespace std; const int N=233333; int cnt,last[N]; int mx[N],dp[N][3],pos[N][2],down[N],give[N]; struct edge{int to,nxt,v;}e[N]; void addedge(int a,int b,int v){e[++cnt]=(edge){b,last[a],v};last[a]=cnt;} void update (int x,int d,int t){ if(d>dp[x][0]){ dp[x][2]=dp[x][1]; dp[x][1]=dp[x][0];pos[x][1]=pos[x][0]; dp[x][0]=d; pos[x][0]=t; } else if(d>dp[x][1]){ dp[x][2]=dp[x][1]; dp[x][1]=d; pos[x][1]=t; } else gmax(dp[x][2],d); } void dfs(int x,int fa){ for(int i=last[x];i;i=e[i].nxt) if(e[i].to!=fa){ dfs(e[i].to,x); int d=dp[e[i].to][0]+e[i].v; gmax(mx[x],mx[e[i].to]); update(x,d,e[i].to); } mx[x]=max(mx[x],dp[x][0]+dp[x][1]); } ll ans=0; void DP(int x,int fa){ update(x,give[x],0); int d1=0,d2=0,p,d; for(int i=last[x];i;i=e[i].nxt) if(e[i].to!=fa){ if(mx[e[i].to]>d1) d2=d1,d1=mx[e[i].to],p=e[i].to; else d2=gmax(d2,mx[e[i].to]); } for(int i=last[x];i;i=e[i].nxt) if(e[i].to!=fa){ if(pos[x][0]==e[i].to) d=dp[x][1]+dp[x][2]; else if(pos[x][1]==e[i].to) d=dp[x][0]+dp[x][2]; else d=dp[x][0]+dp[x][1]; if(e[i].to!=p)gmax(d,d1); else gmax(d,d2); gmax(d,down[x]); ans+=max(mx[e[i].to],d); down[e[i].to]=d; if(pos[x][0]!=e[i].to) give[e[i].to]=dp[x][0]+e[i].v; else give[e[i].to]=dp[x][1]+e[i].v; DP(e[i].to,x); } } int main(){ int T=gi; while(T--){ int n=gi;cnt=ans=0; memset(give,0,sizeof(give)); memset(down,0,sizeof(down)); memset(last,0,sizeof(last)); memset(pos,0,sizeof(pos)); memset(mx,0,sizeof(mx)); memset(dp,0,sizeof(dp)); for(int i=1;i<n;i++){ int a,b,v; a=gi;b=gi;v=gi; addedge(a,b,v); addedge(b,a,v); } dfs(1,1); DP(1,1); printf("%I64d ",ans); } return 0; }
10
题意:做十次n<=100 ,体积<=10^9的01背包。体积和价值随机生成
题解:
搜索QAQ 我先坑着 做作业去了
#include<iostream> #include<stdio.h> #include<stdlib.h> #include<string.h> #include<math.h> #include<algorithm> using namespace std; int n,m,x[110],y[110],a[110][110],f[110]; long long p; inline void dfs(int i,int j,long long k) { if(k>p) p=k; if(i>n || k+(m-j)*double(y[i])/x[i]<p) return; dfs(i+1,j,k); if(!f[i] && j+x[i]<=m) { int l; for(l=i+1;l<=n;l++) f[l]-=a[i][l]; dfs(i+1,j+x[i],k+y[i]); for(l=i+1;l<=n;l++) f[l]+=a[i][l]; } } int main() { int i,j; while(scanf("%d%d",&n,&m)!=EOF) { for(i=1;i<=n;i++) { scanf("%d%d",&x[i],&y[i]); f[i]=0; } p=0; for(i=1;i<n;i++) for(j=i+1;j<=n;j++) if(double(y[j])/x[j]>double(y[i])/x[i]) { swap(x[i],x[j]); swap(y[i],y[j]); } for(i=1;i<n;i++) for(j=i+1;j<=n;j++) if(x[i]<=x[j] && y[i]>=y[j]) { a[i][j]=1; f[j]++; } else a[i][j]=0; for(i=1,j=0;i<=n;i++) if(j+x[i]<=m) { j+=x[i]; p+=y[i]; } //cout<<p<<" "; dfs(1,0,0); cout<<p<<" "; } return 0; }
11
题意:边权为1的无向图,每条边有一个花费,求最小花费使得1~n 最短路每条都被截断
题解:1~n的最短路图上最小割,同bzoj1266 [AHOI2006]上学路线route
我写的 QAQ qnmdSPS错误题面吔屎啦
#include<map> #include<stack> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() #define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout); using namespace std; int n,m; namespace maxf{ const int N=1005,M=233333; struct edge{ int to,next;ll cap; }e[M]; int last[N],cnt=1;int h[N]; void insert(int u,int v,ll cap,ll revc){ e[++cnt]=(edge){v,last[u],cap};last[u]=cnt; e[++cnt]=(edge){u,last[v],revc};last[v]=cnt; } bool bfs(int s,int t){ memset(h,-1,sizeof(h)); h[s]=0; queue<int>q; q.push(s); while(!q.empty()){ int u=q.front();q.pop(); for(int i=last[u];i;i=e[i].next){ if(e[i].cap&&h[e[i].to]==-1){ h[e[i].to]=h[u]+1; q.push(e[i].to); } } } return h[t]!=-1; } ll dfs(int v,int t,ll f){ if(v==t) return f; ll used=0,w=0; for(int u=last[v];u;u=e[u].next){ if(h[e[u].to]==h[v]+1){ w=dfs(e[u].to,t,min(f-used,e[u].cap)); e[u].cap-=w; e[u^1].cap+=w; used+=w; if(used==f) return f; } } if(!used) h[v]=-1; return used; } ll maxflow(int s,int t){ ll ans=0; while(bfs(s,t)){ ans+=dfs(s,t,(1ll<<60)); if(ans>=(1ll<<60))return ans;} return ans; } int main(){ cout<<maxflow(1,n)<<endl; } } namespace graph_theory{ #define M 220000 struct edge{ int to,next,v,cost; }e[M]; #define N 10000 int cnt,last[N],inq[N],dis[N]; //dis:length of shorest path //inq: is point "i" be pushed into the queue void insert(int a,int b,int c,int d){ e[++cnt]=(edge){b,last[a],c,d};last[a]=cnt; } int spfa(int s,int t){ queue<int>q; for(int i=1;i<=N-1;i++)dis[i]=(1e9); q.push(s);dis[s]=0;inq[s]=true; while(!q.empty()){ int c=q.front();q.pop();inq[c]=false; for(int i=last[c];i;i=e[i].next){ if(dis[e[i].to]>dis[c]+e[i].v){ //update dis[e[i].to] dis[e[i].to]=dis[c]+e[i].v; if(!inq[e[i].to]){ q.push(e[i].to); inq[e[i].to]=true; } } } } return dis[t]; } int main(){ memset(last,0,sizeof(last));cnt=1; n=gi;m=gi; for(int i=1;i<=m;i++){ int a,b,c; a=gi;b=gi;c=gi; insert(a,b,1,c); insert(b,a,1,c); } spfa(1,n); memset(maxf::last,0,sizeof(maxf::last));maxf::cnt=1; for(int i=1;i<=n;i++){ for(int j=last[i];j;j=e[j].next){ if(dis[i]+e[j].v==dis[e[j].to]){ maxf::insert(i,e[j].to,e[j].cost,0); } } } return 0; } #undef N #undef M } int main(){ int T=gi; while(T--){ graph_theory::main(); maxf::main(); } }
12
题意:给定50个数(5组)每次询问删除三个数后,剩下的数能否取出不超过十个,和为87
题解:bitset的dp
#include<cstring> #include<bitset> #include<complex> #include<iostream> #include<assert.h> #include<algorithm> using namespace std; #define inf 1001001001 #define infll 1001001001001001001LL #define ll long long #define dbg(vari) cerr<<#vari<<" = "<<(vari)<<endl #define gmax(a,b) (a)=max((a),(b)) #define gmin(a,b) (a)=min((a),(b)) #define Ri register int #define gc getchar() #define il inline il int read(){ bool f=true;Ri x=0;char ch;while(!isdigit(ch=gc))if(ch=='-')f=false;while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=gc;}return f?x:-x; } #define gi read() #define FO(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout); int n; bitset<90>f[110]; int a[101],ans[55][55][55]; bool dp(int x,int y,int z){ for(int i=0;i<=n;i++)f[i].reset(); f[0][0]=1; for(int i=1;i<=n;i++){ if(i==x||i==y||i==z) continue; for(int j=10;j>=1;j--)f[j]|=f[j-1]<<a[i]; } return f[10][87]==1; } int main(){ int t=gi; while(t--){ n=gi; for(int i=1;i<=n;i++)a[i]=gi; for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) for(int k=j;k<=n;k++){ ans[i][j][k]=dp(i,j,k); } int m=gi; while(m--){ int jimmy[4]; for(int i=1;i<=3;i++)jimmy[i]=gi; sort(jimmy+1,jimmy+4); if(ans[jimmy[1]][jimmy[2]][jimmy[3]])puts("Yes"); else puts("No"); } } }