原创
标题:发现环
小明的实验室有N台电脑,编号1~N。原本这N台电脑之间有N-1条数据链接相连,恰好构成一个树形网络。在树形网络上,任意两台
电脑之间有唯一的路径相连。
不过在最近一次维护网络时,管理员误操作使得某两台电脑之间增加了一条数据链接,于是网络中出现了环路。环路上的电脑由于两
两之间不再是只有一条路径,使得这些电脑上的数据传输出现了BUG。
为了恢复正常传输。小明需要找到所有在环路上的电脑,你能帮助他吗?
输入
-----
第一行包含一个整数N。
以下N行每行两个整数a和b,表示a和b之间有一条数据链接相连。
对于30%的数据,1 <= N <= 1000
对于100%的数据, 1 <= N <= 100000, 1 <= a, b <= N
输入保证合法。
输出
----
按从小到大的顺序输出在环路上的电脑的编号,中间由一个空格分隔。
样例输入:
5
1 2
3 1
2 4
2 5
5 3
样例输出:
1 2 3 5
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
本人解题思路:
主要还是要用到 DFS ;目的是在一棵树中,找到一个环路;假定选择在环路中的A结点作为环路的起点,则A结点也可以作为环
路的终点,由于不知哪个结点在环路中,要依次枚举结点 1~N;
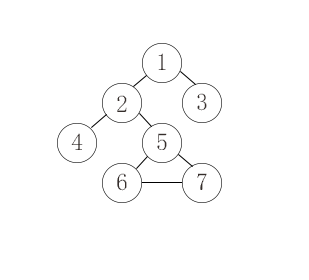
假设用户输入的数据为:
7
1 2 (0)
1 3 (0)
2 4 (0)
2 5 (0)
5 6 (0)
5 7 (0)
6 7 (0)
第三列的(0/1/-1)数码的意义:
0 :此边未遍历
-1:此边经判断不在环上
1:此边在环上
在上图中,5-6-7组成环,现在从结点1(以结点1为起点和终点)开始遍历每条边(边的遍历顺序与用户输入的边的顺序有关);
在遍历过程中只有回到起点时,遍历结束。
搜索用户输入的N行数据,找到有数码1的某行(例子中为第1行),先将此行第三列的数码置1(代表遍历过),再以此行的另
一个结点(例子中为2)为起点,搜索N行数据中数码位为0的行数据(1代表遍历过),停留在第三行,将第三列数码位置1,再
以4为起点继续搜索,此时4为叶子结点,搜索数据未果,所以递归回来将 2 4 (1)——> 2 4 (-1)表示此边定不在环中;此时
再以2为起点继续搜索N行数据,停留在 2 5 (1);再以5为起点继续搜索,停留在 5 6(1),继续搜索停留在 6 7 (1),当停
留在 5 7 (1)的时候,虽然出现了环 5 - 6 - 7,但是不满足以 1 为终点,所以搜索失败(再以7为起点搜索未果);递归回来,
5 7 (-1); 6 7 (-1);5 6 (-1);2 5 (-1);继续以1为起点搜索......所以当以5为第一个起点搜索时,才会搜索成功。
#include<stdio.h> #include<stdlib.h> int arr[100000][3]={0}; //分配3列 int N=0; int flag=0; //flag==1 表示找到起点,返回 int unaccess=0; void dfs(int num,int value){ int i=0; int j=0; for(i=0;i<=N-1;i++){ if(flag==1){ break; } for(j=0;j<=1;j++){ //*************** if(i==N-1 && j==1 && arr[i][j]!=num){ //叶子结点 unaccess=1; break; } if(i==N-1 && j==1 && arr[i][j]==num){ if(arr[i][2]==1){ //叶子结点在第N行,这条边已经遍历过 unaccess=1; break; } } //*************** if(arr[i][j]==num && arr[i][2]==0){ arr[i][2]=1; //*************** if(j==0){ if(arr[i][1]==value){ //判断是不是起点 flag=1; break; } } else{ if(arr[i][0]==value){ flag=1; break; } } //*************** if(j==0){ dfs(arr[i][1],value); if(flag==1){ break; } if(unaccess==1){ arr[i][2]=-1; } unaccess=0; } else{ dfs(arr[i][0],value); if(flag==1){ break; } if(unaccess==1){ arr[i][2]=-1; } unaccess=0; } } } } } int main(){ scanf("%d",&N); int i=0; int j=0; for(i=0;i<=N-1;i++){ for(j=0;j<=1;j++){ scanf("%d",&arr[i][j]); } } for(i=0;i<=N-1;i++){ //最后一列为0代表此边可以走 arr[i][2]=0; } int num=0; for(num=1;num<=N;num++){ // num代表起点和终点 dfs(num,num); if(flag==1){ break; } else{ for(int z=0;z<=N-1;z++){ //以新的起点继续dfs arr[z][2]=0; } } } int *RT; //此数组用来存放环中结点 RT=(int *)malloc(sizeof(int)*(N+1)); for(i=1;i<=N;i++){ RT[i]=0; } for(i=0;i<=N-1;i++){ if(arr[i][2]==1){ RT[arr[i][0]]=1; RT[arr[i][1]]=1; } } for(i=1;i<=N;i++){ if(RT[i]==1){ printf("%d ",i); } } free(RT); return 0; }
有 错误 或 改良方法 欢迎提出。
12:49:48
2018-05-10