设有n个可用作分类的测量值,为了在不降低(或尽量不降低)分类精度的前提下,减小特征空间的维数以减少计算量,需从中直接选出m个作为分类的特征。 问题:在n个测量值中选出哪一些作为分类特征,使其具有最小的分类错误?
从n个测量值中选出m个特征,一共有 中可能的选法。 一种“穷举”办法:对每种选法都用训练样本试分类一下,测出其正确分类率,然后做出性能最好的选择,此时需要试探的特征子集的种类达到 种,非常耗时。 需寻找一种简便的可分性准则,间接判断每一种子集的优劣。 对于独立特征的选择准则 一般特征的散布矩阵准则
对于独立特征的选择准则 类别可分性准则应具有这样的特点,即不同类别模式特征的均值向量之间的距离应最大,而属于同一类的模式特征,其方差之和应最小。 假设各原始特征测量值是统计独立的,此时,只需对训练样本的n个测量值独立地进行分析,从中选出m个最好的作为分类特征即可。

讨论:
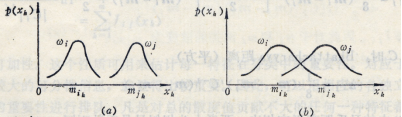
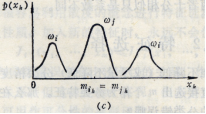
上述基于距离测度的可分性准则,其适用范围与模式特征的分布有关。 三种不同模式分布的情况 (a) 中特征xk的分布有很好的可分性,通过它足以分离i和j两种类别; (b) 中的特征分布有很大的重叠,单靠xk达不到较好的分类,需要增加其它特征; (c) 中的i类特征xk的分布有两个最大值,虽然它与j的分布没有重叠,但计算Gk约等于0,此时再利用Gk作为可分性准则已不合适。 因此,假若类概率密度函数不是或不近似正态分布,均值和方差就不足以用来估计类别的可分性,此时该准则函数不完全适用。

类内、类间的散布矩阵Sw和Sb 类间离散度越大且类内离散度越小,可分性越好。 散布矩阵准则J1和J2形式 使J1或J2最大的子集可作为所选择的分类特征。 注:这里计算的散布矩阵不受模式分布形式的限制,但需要有足够数量的模式样本才能获得有效的结果
