在上一篇博客中分享了尝试用单链表修改程序,虽然在Dev上运行没有错误,但是PTA设置的测试点有几个没有通过,具体不清楚问题出现在哪里,所以现在把之前正确的程序放在这里。
著名的王牌间谍 007 需要执行一次任务,获取敌方的机密情报。已知情报藏在一个地下迷宫里,迷宫只有一个入口,里面有很多条通路,每条路通向一扇门。每一扇门背后或者是一个房间,或者又有很多条路,同样是每条路通向一扇门…… 他的手里有一张表格,是其他间谍帮他收集到的情报,他们记下了每扇门的编号,以及这扇门背后的每一条通路所到达的门的编号。007 发现不存在两条路通向同一扇门。
内线告诉他,情报就藏在迷宫的最深处。但是这个迷宫太大了,他需要你的帮助 —— 请编程帮他找出距离入口最远的那扇门。
输入格式:
输入首先在一行中给出正整数 N(<),是门的数量。最后 N 行,第 我行(1)按以下格式描述编号为 i 的那扇门背后能通向的门:
K D[1] D[2] ... D[K]
其中 K 是通道的数量,其后是每扇门的编号。
输出格式:
在一行中输出距离入口最远的那扇门的编号。题目保证这样的结果是唯一的。
输入样例:
13
3 2 3 4
2 5 6
1 7
1 8
1 9
0
2 11 10
1 13
0
0
1 12
0
0
输出样例:
12
根据题目要求和输入形式,分析数据存储结构,跟树结构相似,所以采用二叉树知识进行解题。
每行序号表示门序号,然后是这个门后面通向其他门个数,再来输入通向那些门。所以这个结构就像一个节点,然后它的孩子个数,跟树结构很像。#include<iostream> #include<queue> using namespace std; typedef struct //结构体数组,一个数据域存放门数量,另外用一个指针指向存放通道门序号的数组 { int doors;//门的数量 int *p; //指向后面门的编号序列 }node; int input(node *a,int n)//读入n扇门的信息 ,并返回跟所在门序号(下标) { int i,j; bool *vi; vi=new bool[n+1];//找出根结点的辅助数组 for(i=0;i<n+1;i++) vi[i]=false; for(i=1;i<n+1;i++) { cin>>a[i].doors; if(a[i].doors)//门后面有通道 { a[i].p=new int[a[i].doors];//申请存储门后面通道 for(j=0;j<a[i].doors;j++) { cin>>a[i].p[j]; vi[a[i].p[j]]=true; } } else //door后面没有通向其他门的通道 { a[i].p=NULL; } } for(i=1;i<n+1;i++)//找出根结点所在下标(起点) { if(!vi[i]) return i; } } int level(node *a,int r)//从a[r]开始对a数组进行层次遍历,并返回遍历最后一个结点的序号 {//跟二叉树层次遍历相似,找到最远的门,也就是层次遍历最后的那个叶结点 queue<int> q; int f,i; q.push(r); while(!q.empty()) { f=q.front(); q.pop(); if(a[f].doors) //t号门后面有通道门 { for(i=0;i<a[f].doors;i++) { q.push(a[f].p[i]); } } } return f;//遍历到最后一个门序号,即是深度最大叶结点 } int main() { node *a;//用于存储整棵树 int n,root; cin>>n; a=new node[n+1]; root=input(a,n); // cout<<root; cout<<level(a,root); return 0; }
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。
例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
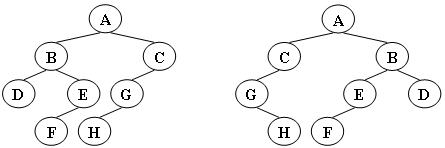 图1
图1 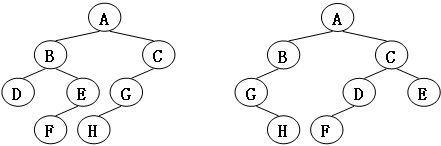 图2
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
这道题再次用到查找树的根结点的函数,跟之前完全一样,主要实现操作在于判断树同构的算法。
有以下几种情况:
1、两棵树为空,则同构
2、有一棵树为空,则不同构
3、都不为空,但是根结点名称不同,则不同构
4、都不为空,同构时的符合情况:
(1)左1=左2 且 右1=右2
(2)左1=右2 且 右1=左2
第4步判断操作可以基于前面3点,用递归方式实现。
#include<iostream> #include<queue> using namespace std; typedef struct { char name; int l,r; } node; int BuildTree(node T[]) //建立二叉树 { int i,N; bool check[100]={false};//check数组用于查找树的根节点 char x,y; cin>>N; if(N)//树结点个数不为0 { for(i=0;i<N;i++) { cin>>T[i].name>>x>>y; if(x!='-')//若结点不为空,将节点索引放入左子树结点 { T[i].l=x-'0'; check[T[i].l]=true;//记录此结点索引,在check数组将该位置置为true } else { T[i].l=-1;//若结点为空,将其置为-1 } if(y!='-')//同上,放入右子树 { T[i].r=y-'0'; check[T[i].r]=true; } else { T[i].r=-1; } } for(i=0;i<N;i++)//遍历check数组,除了根结点之外,其它元素为true或-1 { if(!check[i]) return i;//返回根结点下标 } } else return -1;// 若树为空,返回 -1 } int treetonggou(node t1[],node t2[],int x,int y)//判断两棵树是否同构 { if(x==-1&&y==-1) return 1;//两棵树为空,同构 else if(x==-1||y==-1) return 0;//有一棵树为空,不同构 else if(t1[x].name!=t2[y].name) return 0;//根结点名称不同,不同构 else//递归判断所在根结点是否符合 { return((treetonggou(t1,t2,t1[x].l,t2[y].l))&&(treetonggou(t1,t2,t1[x].r,t2[y].r))//判断两棵树此结点情况:左=左并且右=右 ||(treetonggou(t1,t2,t1[x].l,t2[y].r))&&(treetonggou(t1,t2,t1[x].r,t2[y].l)));//左=右并且右=左 } } int main() { node t1[100],t2[100]; int r1,r2; r1=BuildTree(t1); r2=BuildTree(t2);//cout<<r1<<" "<<r2; //cout<<treetonggou(t1,t2,r1,r2); if(treetonggou(t1,t2,r1,r2)) cout<<"Yes"; else cout<<"No"; return 0; }
做这道题开始不是很顺利,问题出在我用递归方式不对,在第4步时候是这样的:
int treetonggou(node t1[],node t2[],int x,int y) { if(x==-1&&y==-1) return 1; else if(x==-1||y==-1) return 0; else if(t1[x].name!=t2[y].name) return 0; else { if((treetonggou(t1,t2,t1[x].l,t2[y].l))&&(treetonggou(t1,t2,t1[x].r,t2[y].r))) return 1; if((treetonggou(t1,t2,t1[x].l,t2[y].r))&&(treetonggou(t1,t2,t1[x].r,t2[y].l))); return 1; } }
看是用了递归函数,之后一分析,其实没有用到前面基础进行递归,而是有自己的返回值了,没有用到递归的思想,在几个测试点没通过,因为没有考虑到各种情况,比如:
遍历结果相同,但树不同构;孩子结点相同,但根结点不同,树不同构。
之后几次修改,得到上面那个很长的return语句,最后通过。