哈哈,先原谅这一个月在重围中的借口。有几次想起还有blogs这件事,也是觉得可能这个月没有publication留下。结果刚才debug发现了些有趣的事情,当然,现象是表面,insight是关键。由此的事情远没有完成,先在这里记下,探索也是部分的需要计划的:)
Introduction
事情源于之前做的一个分类问题,由于牵涉了新设想的结构和函数,于是只是在固定的极小样本集里面先train一下,看看是否能够达到饱和。但是从后面的结果来看,acc在0.6-0.7范围中就停止了(由于样本数量只有128个作为一次性的batch-data输入,进行多次的反复update,检查了abs-Grad-sum,发现在长时段内趋于0)。
Debug
最开始,我以为是容量不够,于是扩大了宽度,发现效果轻微;后面又引入低层的特征进行扩容尝试,收获了相同的结果。
今天下午又拿出来试了下,却意外的把GradBlock放在了这个子项(classification)的最终激活函数之后(后面检查时才发现的),结果发现很快就收敛到饱和状态。
检查了几遍系统后,我只将Block那行注释,确定系统不能达到饱和。于是开始关注激活层,用tanh替换了所有夹在预训练model的conv层以外的relu,并取消对Grad的Block,发现系统较快的就达到饱和(在abs-Grad-sum还没有低于10的时候);之后有将系统逐渐缩小参数规模,发现在最开始的规模上,同样可以达到饱和。
Proposal
一些观点需要在这里整理。
Observations
先来整理下调试的路径。
- 一个比较关键的现象是切断Grad在最末的激活函数与后续(全连接)的系统后,系统出现了预期的饱和状态;
- 另外,替换relu为tanh后,系统收敛较慢,但依然在短期内到达饱和。
- 全部使用relu,在更长时间的将abs-Grad-sum趋于0的尝试的末尾,依然收敛在较低水平。
Note
在这里说些看法。
从以上的Debug中,容易产生这样的想法,问题的产生源于两种激活函数的不同。但具体是怎样的一种特性解释,需要讨论。
一种想法是,relu的死区使大量单元陷入,导致性能下降,这种看法可能成立(后面与大师兄谈论,大师兄的第一反应是relu的死区丢失了信息);但1的观测说明在relu之前的系统即使通过随机初始化,后面的信息也是足够用来使之饱和。
另一种,想法是:不可导的特性,使以此激活函数为节点的前后两个子系统在梯度下降的优化策略中,出现了前后不一致。
后续的系统通过梯度计算出前面的系统应该做出的调整,但后向传播通过relu时却带上了某种程度的不可预见性(不能根据梯度信息来确定调整后会出现的状态),造成的结果就是优化过程变得不稳定(可能前后一致性不统一听起来更慎重),也就是说前后子系统的优化方向发生偏差。
另外,从最终收敛,但性能较低的情况看,死区的存在也是有贡献的。
About relu
说道此处,顺带说下,我对relu于分类问题的看法。
还想得起之前在毕业设计文中,写到不动点映射特性是解决分类问题的关键(当时还没有了解到relu的存在)。而relu正是具备这样的特性,死区的存在使得有更大的机会进行不动点映射系统的构建。稍微牵强些,是否可以认为这种特性正好是利于进行特征提取的?而对分类问题可能还需要对特征的敏感性?但这样看,对于分类问题,到底是否还是一个单纯的不动点映射问题?
在这种观点下,是否可以认为relu类的带有某种不动点特性的函数,更适宜进行定性,而于回归问题,存在这缺陷;
Future Works
还有些路径需要执行才能验证上文的部分猜测。
- 替换relu为leaky-relu,重新测试
若干未列明,跑路要紧。。。
Oct 31, 2017
今早试了下用leaky-relu进行替换的试验。
LeakyReLU
按照昨天的观点,由于函数导数的不连续性,后向传播方式下的梯度优化将产生不稳定现象。
看到结果之前我的猜测是中途可能出现不稳定,但由于死区特性得到了弱化,在后期会出现收敛(饱和)。但结果却出现了Gradient Explosion,以下是每次更新后,计算的abs-Grad-sum结果:
INFO: 2017-10-31 09:56:14,343 clip.py [line: 7] gradient sum: 2570469.820984
INFO: 2017-10-31 09:56:18,898 clip.py [line: 7] gradient sum: 7628072.981415
INFO: 2017-10-31 09:56:23,442 clip.py [line: 7] gradient sum: 104128273.523438
INFO: 2017-10-31 09:56:27,982 clip.py [line: 7] gradient sum: 1003394306.062500
INFO: 2017-10-31 09:56:32,531 clip.py [line: 7] gradient sum: 26595445776.000000
INFO: 2017-10-31 09:56:37,070 clip.py [line: 7] gradient sum: 82864352460.000000
INFO: 2017-10-31 09:56:41,611 clip.py [line: 7] gradient sum: 2485723173798.000000
INFO: 2017-10-31 09:56:46,155 clip.py [line: 7] gradient sum: 14795568299674.000000
INFO: 2017-10-31 09:56:50,706 clip.py [line: 7] gradient sum: 340887166279834.000000
INFO: 2017-10-31 09:56:55,246 clip.py [line: 7] gradient sum: 1506918417760358.000000
INFO: 2017-10-31 09:59:05,430 clip.py [line: 7] gradient sum: 119767988743176352.000000
INFO: 2017-10-31 09:59:09,977 clip.py [line: 7] gradient sum: 217811190464643200.000000
INFO: 2017-10-31 09:59:14,519 clip.py [line: 7] gradient sum: 9045955479473225728.000000
INFO: 2017-10-31 09:59:19,065 clip.py [line: 7] gradient sum: 48279445897211805696.000000
INFO: 2017-10-31 09:59:23,603 clip.py [line: 7] gradient sum: 1324136950814446977024.000000
INFO: 2017-10-31 09:59:28,138 clip.py [line: 7] gradient sum: 6650622893084393865216.000000
INFO: 2017-10-31 09:59:32,678 clip.py [line: 7] gradient sum: 137297709636549848596480.000000
INFO: 2017-10-31 09:59:37,218 clip.py [line: 7] gradient sum: 1513821207037384203436032.000000
INFO: 2017-10-31 09:59:41,755 clip.py [line: 7] gradient sum: nan
INFO: 2017-10-31 09:59:46,290 clip.py [line: 7] gradient sum: nan
这个试验,我在不同时间测试了两次,最终结果是一致的。看来不稳定状态是存在的,但最终却成了误差振荡器。
对比relu和leaky的结果,更容易使人相信的是,前者没有产生Explosion的原因很有可能是,严格死区的存在使系统保持了性质上的稳定;而leaky中,负向性质的死区,给系统埋下了震荡的机会。
从以上讨论来看,在relu的不饱和情况中,有较大的可能,收敛时relu的输出几乎全部为0,关于此一点可以参考,abs-Grad-sum为0。
我检查了下,收敛时histogram分布大致是这样的:
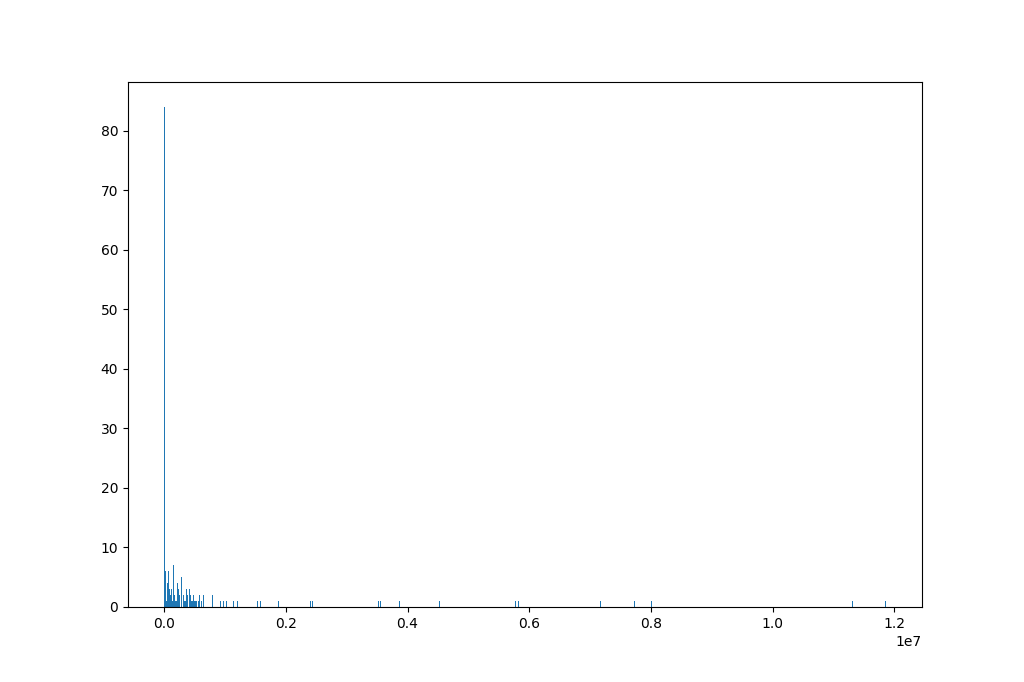 *Fig-1:Histogram of relu's output(x ranges from .1 to max)*
*Fig-1:Histogram of relu's output(x ranges from .1 to max)*
这个分布横坐标起止:[.1,max],用以对比0的统计量。
 *Fig-2: Histogram of relu's (-.1 to .1)*
*Fig-2: Histogram of relu's (-.1 to .1)*
此分布横坐标起止:[-.1,.1]。已经可以看出,明显地就放在0上。
另外,从Fig-1中,了解到,已经出现极大的相应值了,说明这个系统已经废掉。
Batch-Normalization
从原理上看,BN相当于一个阻尼器,防止参数过快的变化。所以可以部分地预计到,使用BN后优化过程将会更接近理想状况。从试验上来看,在conv之后,引入BN,再接入Leaky-/ReLU,两者都可以达到饱和。这一点,印证了前述的不稳定预计。
先这样吧。