大致题意: 给定平面上(n)个点,求最大的矩形面积。
暴力
显然,一个矩形两条对角线中点坐标相等、长度相等。
于是我们暴力枚举两点作为一条对角线,然后把中点坐标的两倍、长度的平方存储下来(用整数避免精度)。
接着我们枚举每一对能构成一个矩形的对角线,计算其面积。
考虑一个矩形长成这个样子:(图中红色部分)
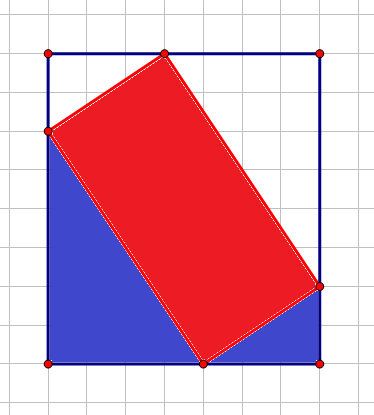
显然它的面积就是大矩形(横坐标最大值与最小值的差值×纵坐标最大值与最小值的差值)减去蓝色部分的两倍(取一条对角线的两点分别与另一条对角线的一点取坐标差计算直角三角形面积)。
具体实现详见代码。
代码
#include<bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int&
#define I inline
#define W while
#define N 1500
#define LL long long
using namespace std;
int n,a[N+5],b[N+5];
struct data
{
int i,j,x,y;LL l;I data(CI p=0,CI q=0,CI a=0,CI b=0,LL t=0):i(p),j(q),x(a),y(b),l(t){}
I bool operator < (Con data& o) Con {return x^o.x?x<o.x:(y^o.y?y<o.y:l<o.l);}//排序
I bool operator == (Con data& o) Con {return x==o.x&&y==o.y&&l==o.l;}//判相等
}s[N*N+5];
int main()
{
RI i,j;for(scanf("%d",&n),i=1;i<=n;++i) scanf("%d%d",a+i,b+i);
#define sqr(x) 1LL*(x)*(x)
RI cnt=0;for(i=1;i^n;++i) for(j=i+1;j<=n;++j)//枚举两点作为对角线
s[++cnt]=data(i,j,a[i]+a[j],b[i]+b[j],sqr(a[i]-a[j])+sqr(b[i]-b[j]));
RI x,y;RI XMx,XMn,YMx,YMn;LL S1,S2,t,ans=0;
for(sort(s+1,s+cnt+1),i=1;i<=cnt;i=j+1)//枚举对角线
{
for(j=i;j<=cnt&&s[i]==s[j+1];++j);//找到所有能构成一个矩形的对角线
for(x=i;x^j;++x) for(y=x+1;y<=j;++y)//枚举
XMx=max(max(a[s[x].i],a[s[x].j]),max(a[s[y].i],a[s[y].j])),//横坐标最大值
XMn=min(min(a[s[x].i],a[s[x].j]),min(a[s[y].i],a[s[y].j])),//横坐标最小值
YMx=max(max(b[s[x].i],b[s[x].j]),max(b[s[y].i],b[s[y].j])),//纵坐标最大值
YMn=min(min(b[s[x].i],b[s[x].j]),min(b[s[y].i],b[s[y].j])),//纵坐标最小值
S1=abs(1LL*(a[s[x].i]-a[s[y].i])*(b[s[x].i]-b[s[y].i])),//一个直角三角形面积两倍
S2=abs(1LL*(a[s[x].j]-a[s[y].i])*(b[s[x].j]-b[s[y].i])),//另一直角三角形面积两倍
ans<(t=1LL*(XMx-XMn)*(YMx-YMn)-S1-S2)&&(ans=t);//大面积减小面积
}return printf("%lld",ans),0;
}