算法正则化可以有效地防止过拟合, 但正则化跟算法的偏差和方差又有什么关系呢?下面主要讨论一下方差和偏差两者之间是如何相互影响的、以及和算法的正则化之间的相互关系
假如我们要对高阶的多项式进行拟合,为了防止过拟合现象,我们要使用图下所示的正则化。因此我们试图通过下面的正则化项,来让参数的值尽可能小。正则化项的求和范围,照例取为j等于1到m,而非j等于0到m。

然后我们来分析以下三种情形。第一种情形:正则化参数lambda取一个比较大的值(比如lambda的值取为10000甚至更大)。在这种情况下,所有这些参数,包括theta1,包括theta2,包括theta3等等,将被大大惩罚。其结果是这些参数的值将近似等于0,并且假设模型h(x)的值将等于或者近似等于theta0的值,因此我们最终得到的假设函数应该是近似一条平滑的直线。因此这个假设处于高偏差,对数据集欠拟合。因此这条水平直线,对这个数据集来讲不是一个好的假设模型。

与之对应的另一种情况:lambda值很小(比如说lambda的值等于0,如下图)。在这种情况下,如果我们要拟合一个高阶多项式的话,此时我们通常会处于过拟合的情况。在这种情况下,拟合一个高阶多项式时,如果没有进行正则化,或者正则化程度很微小的话,我们通常会得到高方差和过拟合的结果。通常来说,lambda的值等于0,相当于没有正则化项,因此是过拟合假设。
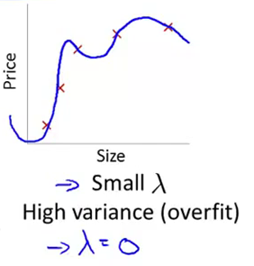
只有当我们取一个中间大小的lambda值时(如下图),我们才会得到一组合理的,对数据刚好拟合的theta参数值。
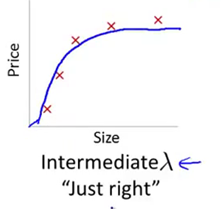
那么我们应该怎样自动地选择出一个最合适的正则化参数lambda呢?
假设在使用正则化的情形中,定义Jtrain(θ)为另一种不同的形式。目标同样是最优化,但不使用正则化项。在前面的介绍中,当我们没有使用正则化时,我们定义的Jtrain(θ) 就是代价函数J(θ)。但当我们使用正则化多出这个lambda项时,我们就将训练集误差(Jtrain)定义为训练集数据预测的平方误差的求和。或者准确的说,是训练集的平均误差平方和,但不考虑正则化项。与此类似,我们定义交叉验证集误差以及测试集误差为:对交叉验证集和测试集进行预测,取平均误差平方和的形式。我们对于训练误差Jtrain、交叉验证集误差Jcv,和测试集误差Jtest的定义都是平均误差平方和。或者准确地说,是训练集、验证集和测试集进行预测,在不使用正则化项时,平均误差平方和的二分之一。
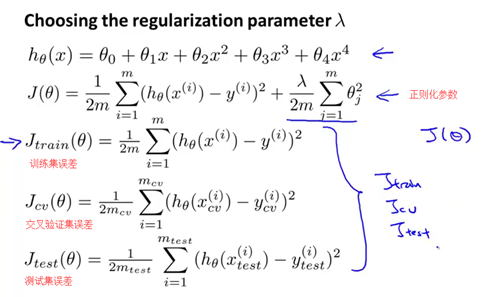
下面是我们自动选取正则化参数lambda的方法。通常做法是选取一系列想要尝试的lambda值(比如是0.01,0.02,0.04等等),通常来讲,一般将步长设为2倍速度增长,一直到一个比较大的值。以两倍步长递增的话,最终取值10.24,实际上我们取的是10,但取10已经非常接近了。小数点后的0.24,对最终的结果不会有太大影响。因此,这样就得到了12个不同的正则化参数lambda对应的12个不同的模型。我们将从这个12个模型中选出一个最合适的模型,当然,我们也可以试小于0.01或者大于10的值。得到这12组模型后,接下来我们要做的事情是选用第一个模型(也就是lambda等于0),最小化代价函数J(θ)。这样我们就得到了某个参数向量theta,与之前做法类似,我使用theta上标(1)来表示第一个参数向量theta。然后再取第二个模型,也就是lambda等于0.01的模型,最小化代价方差,那么会得到一个完全不同的参数向量theta(2),同理,会得到theta(3)对应第三个模型,以此类推,一直到最后一个lambda等于10或10.24的模型,对应theta(12)。接下来就可以用所有这些假设,所有这些参数,以及交叉验证集来评价它们了。因此我们可以从第一个模型、第二个模型等等开始,对每一个不同的正则化参数lambda进行拟合。然后用交叉验证集来评价每一个模型,也即测出每一个参数thata在交叉验证集上的平均误差平方和。然后我就选取这12个模型中交叉验证集误差最小的那个模型作为最终选择。对于本例而言,假如说最终选择了theta(5),也就是五次多项式,因为此时的交叉验证集误差最小。做完这些,如果想看看该模型在测试集上的表现,我们可以用经过学习得到的模型theta(5) 来测出它对测试集的预测效果。这里我们依然用交叉验证集来拟合模型。这也是为什么我们之前预留了一部分数据作为测试集的原因。这样就可以用测试集比较准确地估计出参数向量theta对于新样本的泛化能力。这就是模型选择在选取正则化参数lambda时的应用。

最后一个问题是,当我们改变正则化参数lambda的值时,交叉验证集误差和训练集误差会随之发生怎样的变化。我们最初的代价函数J(θ) 是这样的形式(如下图)

但在这里我们把训练误差定义为不包括正则化项,交叉验证集误差也定义为不包括正则化项(如下图)
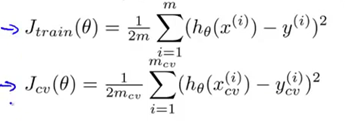
我们要做的是绘制出Jtrain和Jcv的曲线。随着我们增大正则化项参数lambda的值,我们的假设在训练集上以及在交叉验证集上的表现如何变化。就像我们之前看到的,如果正则化项参数lambda的值很小,也就是说我们几乎没有使用正则化,有很大可能处于过拟合。而如果lambda值取的很大的时候(也就是说取值在横坐标的右端,如下图),很有可能处于高偏差的问题。所以,如果画出Jtrain和Jcv的曲线,就会发现当lambda的值取得很小时,对训练集的拟合相对较好,因为没有使用正则化。因此,对于lambda值很小的情况,正则化项基本可以忽略。我们只需要对平方误差做最小化处理即可。当lambda增大时,训练集误差Jtrain的值会趋于上升。因为lambda的值比较大时,对应着高偏差的问题,此时连训练集都不能很好地拟合。反过来,当lambda的值取得很小的时候,数据能随意地与高次多项式很好地拟合。交叉验证集误差的曲线是这样的(下图紫红色曲线),在曲线的右端,当lambda值取得很大时,我们会处于欠拟合问题,也对应着偏差问题。那么此时交叉验证集误差将会很大,这是交叉验证集误差Jcv。由于高偏差的原因我们不能很好地拟合,我们的假设不能在交叉验证集上表现地比较好。而曲线的左端对应的是高方差问题,此时我们的lambda值取得很小很小,因此我们会对数据过度拟合。所以由于过拟合的原因,交叉验证集误差Jcv结果也会很大。前面就是当我们改变正则化参数lambda的值时,交叉验证集误差和训练集误差随之发生的变化。在中间取的某个lambda的值表现得刚好合适,交叉验证集误差或者测试集误差都很小。
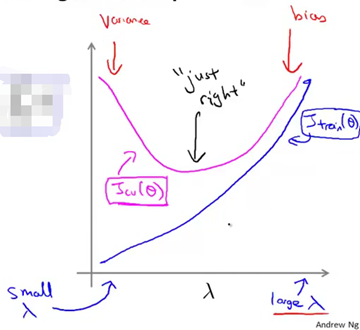
当然在这里画的图显得太卡通也太理想化了。对于真实的数据你得到的曲线可能比这看起来更凌乱,会有很多的噪声。通过绘出交叉验证集误差的变化趋势曲线,可以选择出或者编写程序自动得出能使交叉验证集误差最小的那个点,然后选出那个与之对应的参数lambda的值。当我们在尝试为学习算法选择正则化参数lambda的时候,通常都会得出类似上图的结果,帮助我们更好地理解各种情况,同时也帮助我们确认选择的正则化参数值好不好。