归并排序法
参考文章:
https://zh.wikipedia.org/wiki/Category:%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95
https://www.cnblogs.com/chengxiao/p/6194356.html
https://zh.wikipedia.org/wiki/%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F
基本思想:
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略。
分治法将问题分(divide)成一些小的问题后求解,而治(conquer)的阶段则将分的阶段得到的各答案"集成"在一起,因此叫分而治之。
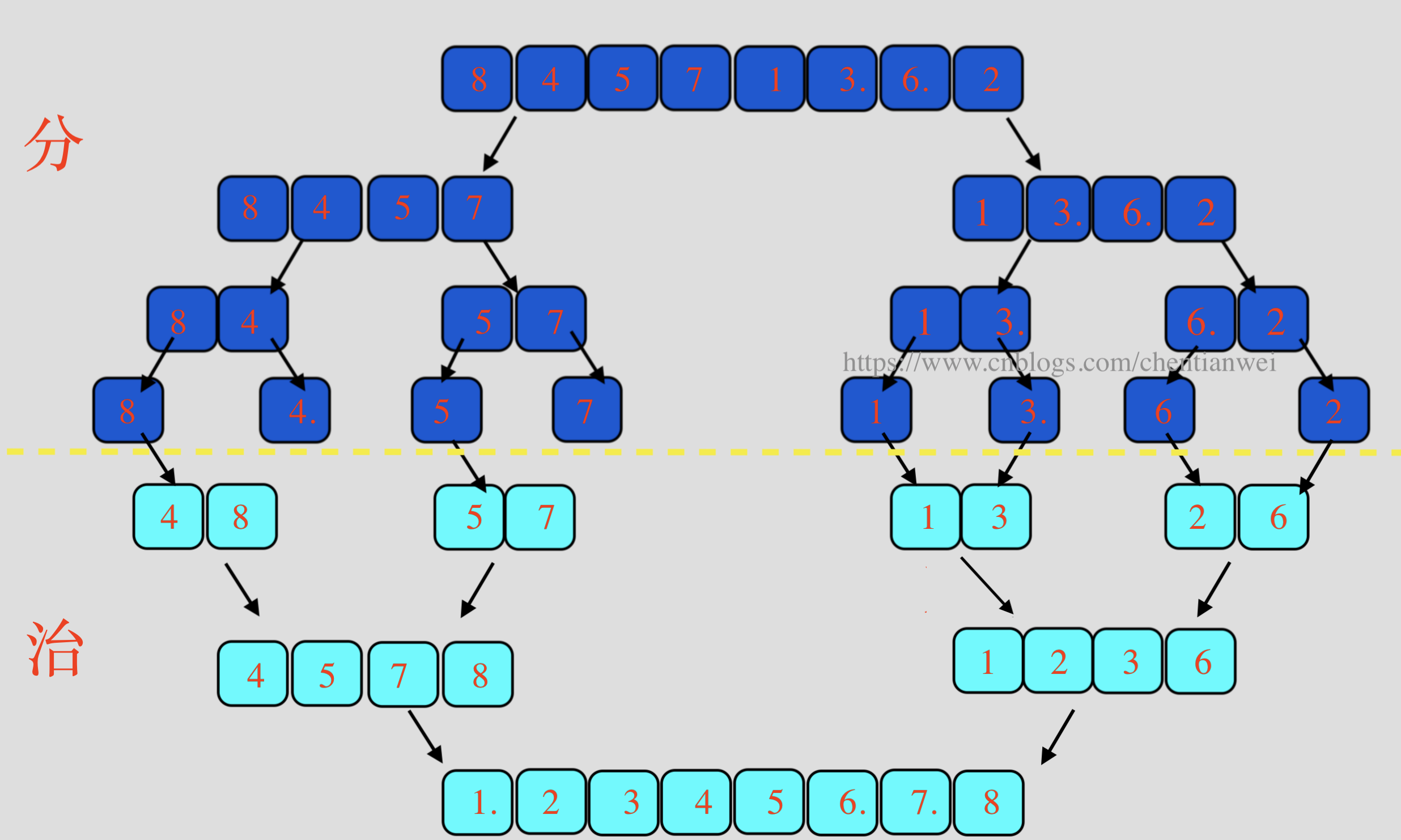
由图可以看到,这种结构很像一棵二叉树。“分”阶段可以理解为递归拆分子序列的过程。递归的深度h = lgN。
时间复杂度最好最坏都是
实现归并排序的2种方法:
递归法(Top-down)
- 申请空间merge,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列。
- 设定两个指针p1和p2,最初位置分别为两个已经排序序列的起始位置left[0], right[0]。
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置。
- 如果是序列是数组结构,也可以不动指针,而是进行删除操作。即每次比较后,把被移动第一个元素的那个数组,使用shift方法删除被移动的第一个元素,然后继续这比较,left[0] <=> right[0]。但是⚠️,数组删除第一个元素导致它从新分配指针给每个数组元素,需要花费时间。所以还是使用移动指针的方法好✌️。
- 被移动指针的序列,是那个有相对较小的元素的序列。
- 重复步骤3直到其中一个指针到达序列尾。
- 将另一序列剩下的所有元素直接复制到合并序列merge的尾巴。
function merge(left, right){ var result = []; //使用指针能提高速度。不使用shift方法,因为数组会重新分配指针,导致多花费时间。 while(left.length > 0 && right.length > 0){ if(left[0] < right[0]){ result.push(left.shift()); }else{ result.push(right.shift()); } } return result.concat(left, right); } function mergeSort(arr){ if(arr.length <=1) return arr; var middle = Math.floor(arr.length / 2); var left = arr.slice(0, middle); var right = arr.slice(middle); return merge(mergeSort(left), mergeSort(right)); }
或者使用指针(比较麻烦):
function merge(left, right){ var result = []; //改用指针 var i = 0; var j = 0; // 当指针i或者j增长到大于最后一个元素index的时候,结束循环。 left.length - 1就是最后一个元素的索引 while( (left.length - 1) >= i && (right.length - 1) >= j ) { if(left[i] < right[j]) { result.push(left[i]) i = i + 1 } else { result.push(right[j]) j = j + 1 } } //把剩下的数组合并到result if ( left.length == i) { return result.concat(right[j]) } else { return result.concat(left[i]) } }
ruby的实现:见git
迭代法(Bottom-up)
原理如下(假设序列共有{displaystyle n}
- 将序列每相邻两个数字进行归并操作,形成{displaystyle ceil(n/2)}
个序列,排序后每个序列包含两/一个元素
- 若此时序列数不是1个则将上述序列再次归并,形成{displaystyle ceil(n/4)}
个序列,每个序列包含四/三个元素
- 重复步骤2,直到所有元素排序完毕,即序列数为1
迭代法,就是从下往上。
总结:
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。
每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)