Segment tree
Wiki(翻译)
一种静态树的数据结构。用于储存intervals, segments。它可以查询储存的segments。
在原理上,这个结构建立后就不能修改。
翻译称为“线段树”。
线段树储存 a set I of n intervals, 创建的时间复杂度O(n log n).
它搜索k个intervals的时间复杂度是O(log n + k)
它的使用领域:
在计算几何学和地理数据系统 computational geometry, and geographic information systems.
线段树能够被概括到高纬领域“The segment tree can be generalized to higher dimension spaces.”
英文文章的理解
Segment tree用在数组的范围查询和这个数组的元素修改。例如,查询一个数组的一段(从索引L到R)的所有元素的和, 或者它的查询最小值查询。
个人认为,线段树就是对一个超长数组的预先计算,比如范围求和,求最/小大值。把这些结果存储在线段树节点内,当需要查询的时候,无需遍历数组,而是以更快的速度O(lgN),从线段树内得到查询结果。
什么是线段树?
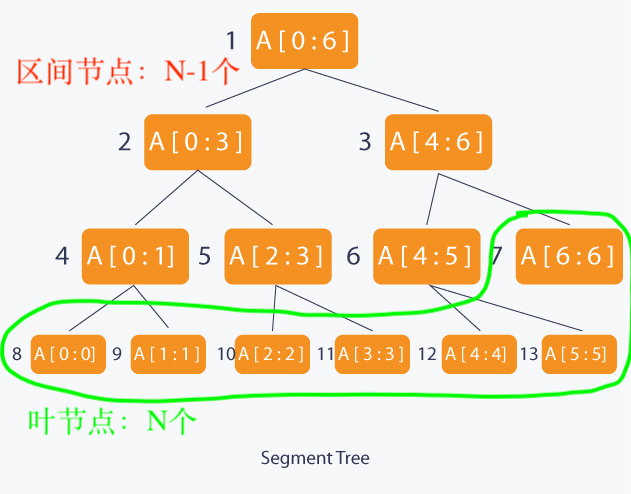
一个二叉树。每个节点是一个线段interval/或者叫区间segment。
假如一个数组A, 长度为N, 使用线段树T:
- T的root是整个数组A[0: N-1],即整个数组的sum。
- 每个叶节点代表单个元素A[i], 0=< i < N
- 每个内部节点代表一段区间A[i: j], 就是从A[i]到A[j]的和sum。
根节点代表整个数组。然后被分开成2部分区间,分别代表左儿子和右儿子。
每个父节点和子节点的关系,都是这样的。所以线段树的高度(时间复杂度)是 O(lg N)。
N个叶节点代表N个数组的元素。非叶节点的数量为N-1。因此全部节点的数量为2*N - 1。
线段树被建立后,结构就不能修改了。但可以修改节点的值,因此它可以有2类操作:
- Update: 更新数组元素A, 并在线段树上做出相应的变化。
- Query:可以查询一个区间并返回结果(指定区间,求最大/小值,求和)
操作
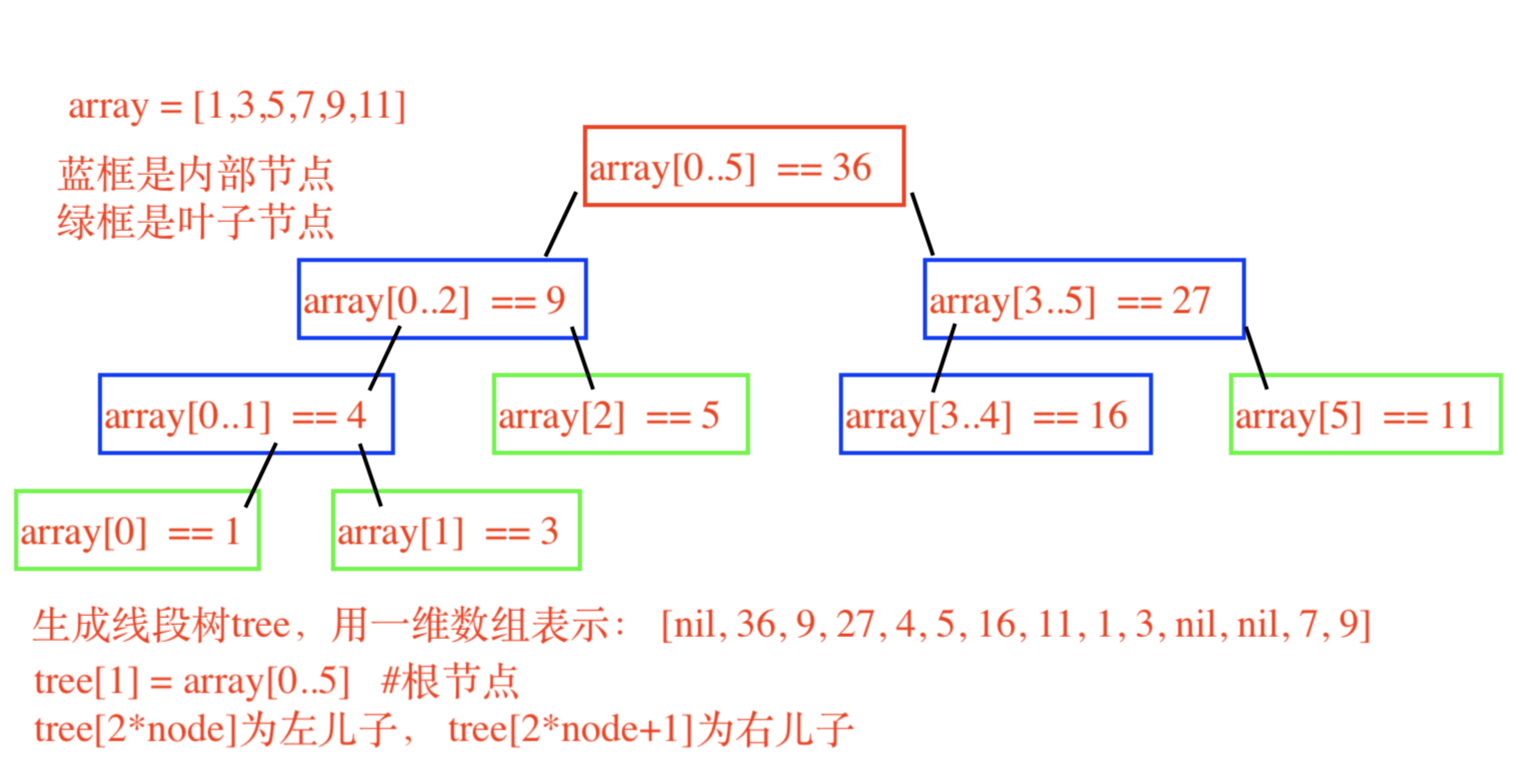
既然线段树是一个二叉树,那么一个一纬数组就可以代表它。tree = [], 然后构建线段树后,tree的元素存储root/内节点/叶子节点的值。
其中:
tree[1] = array[0..6]
tree[2] = array[0..3]
tree[3] = array[4..6]
...略
建立Segment-tree
首先,确认“节点内储存什么数据?”的问题。例如:如果问题是查找一段区间的元素的和sum,那么每个非叶子节点储存它的儿子节点的数据的和sum。
然后,使用递归方法建立树结构。因为叶节点储存数组元素,所以在递归回归的过程中,通过儿子节点的值相加得到父亲节点的值。
代码见下:
tree[1] == A[0..6]
void build(int node, int start, int end) #node代表节点编号。 { if(start == end) { // Leaf node will have a single element, A代表数组。 tree[node] = A[start]; } else { int mid = (start + end) / 2; // Recurse on the left child,建立左儿子节点,并在回归时,返回它自身。 build(2*node, start, mid); // Recurse on the right child build(2*node+1, mid+1, end); // Internal node will have the sum of both of its children。父节点的值:sum。 tree[node] = tree[2*node] + tree[2*node+1]; } }
ruby代码的实现:
array = [1,3,5,7,9,11] # 用tree来存线段树。 tree = [] def build(node, start, tail, array, tree) # 判断是否是叶节点,然后把数组array的元素存入线段树的叶节点。 if start == tail tree[node] = array[start] else mid = (start + tail)/2.to_i # 建立左儿子和右儿子 build(2*node, start, mid, array, tree) build(2*node + 1, mid + 1, tail, array, tree) # 递归的回归过程中(bottom_up),计算内节点的值 tree[node] = tree[2*node] + tree[2*node +1] end end build(1, 0, array.size - 1 , array, tree)
p tree
#结果是:
# [nil, 36, 9, 27, 4, 5, 16, 11, 1, 3, nil, nil, 7, 9]
小结:
线段树可以使用递归方法建立Recursion(bottom-up 方法)。从root向下形成树结构,再从叶节点一路向上到root,更新从叶节点到root的过程中的节点的值。
每一步,2个儿子节点形成它们的父节点。每个内部节点都代表它们儿子区间的合成。最后递归在root完成,root代表了了整个array的sum。
Update
代码和构建代码的过程类似,都是从root开始,根据元素的index,从root开始判断,找到它所在的叶节点。
然后,更新叶节点的值,并返回叶节点的值给父节点,然后一路向上,回归的过程中更新内部节点。
时间
def update(node, start, tail, idx, val, tree) if start == tail tree[node] = val return end # 判断idx在左子树还算右子树 mid = (start + tail)/2.to_i if start <= idx && idx <= mid update(2*node, start, mid, idx, val, tree) else update(2*node + 1, mid+1, tail, idx, val, tree) end tree[node] = tree[2*node] + tree[2*node +1] end build(1, 0, array.size - 1 , array, tree) p tree #结果是: # [nil, 36, 9, 27, 4, 5, 16, 11, 1, 3, nil, nil, 7, 9] # 更新array的元素 array[1] == 2 array[1] = 2 # 更新线段树 update(1, 0, array.size - 1, 1, 2, tree) p tree #结果: [nil, 35, 8, 27, 3, 5, 16, 11, 1, 2, nil, nil, 7, 9] # tree[9] 即array[1]
Query
范围查询是线段树结构的优势。时间复杂度lgN。
方法:
假如想要得到从L到R的范围的array的元素的sum。首先,从root开始递归,并检查内部节点是否在范围(L to R)内。然后,判断有几种情况:
- 要查询范围正好和节点的范围完全重合(start == L && R == tail),直接返回节点的值。
- 要查询范围完全不在节点的范围内(不相交) ( R <start || L > tail),返回值0即可。
- 要查询范围在节点的范围内部(被包含)(start < L && R < tail),继续向下递归查询。
- 要查询范围包含了节点的范围 (包含),(L < start && tail < R), 直接返回节点的值。
- 要查询范围部分在节点的范围内 (部分相交),继续向下递归查询。
经过整理其实就三种情况:
- L <= start && tail <= R, 返回node的值
- R <start || L > tail, 返回0
- 其他2种:部分相交和要查询范围在节点范围内(但不重合)的情况。继续向下递归
还使用上面的例子:数组array, 用户想要查询array[2]到array[4]的sum。怎么通过线段树结构计算sum?
代码:
# node为当前查找的节点的在线段树的索引 # queryL, 用户查找的左边界 # queryR, 用户查找的右边界 def query(node, start, tail, queryL, queryR) # 不相交,返回0 if queryR < start || tail < queryL return 0 # 查询范围包含(或完全重合)了当前节点的范围。 elsif queryL <= start && tail <= queryR return tree[node] else #其他情况:部分相交和要查询范围在节点范围内(但不重合)的情况,递归: mid = (start + tail)/2.to_i p1 = query(2*node, start, mid, queryL, queryR) p2 = query(2*node + 1, mid + 1, tail, queryL, queryR) return p1 + p2 end end
对一段数组来说,按它的基本结构:求和操作的话花费O(N)时间;更新元素的值花费O(1)
换成线段树结构后:
根据需求构建它使用O(N), 完全更新一个元素是O(logN), query是O(logN)。
参考: