69. x 的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。
解题思路
本题应该还加一个要求, 不允许直接开根号得出结果
方法一: 袖珍计算器算法
[sqrt{x}=x^{1 / 2}=left(e^{ln x}
ight)^{1 / 2}=e^{frac{1}{2} ln x}
]
根据以上公式, 可以替代直接根号的运算。但是这样计算的结果, 可能会带有误差。有精度丢失导致值偏小的可能性。所以在返回结果时, 需要把ans+1拿来尝试一次。
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
int ans = (int) Math.exp(0.5 * Math.log(x));
return (long) (ans + 1) * (ans + 1) <= x ? ans + 1 : ans;
}
方法二: 二分法
找整数x, x+1,使得x ^ 2 <= n 并且(x+1)^2 > n。可使用二分的方法来查找。二分的初始下界是0, 初始上界是N。
public int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long) mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
方法三: 牛顿迭代法
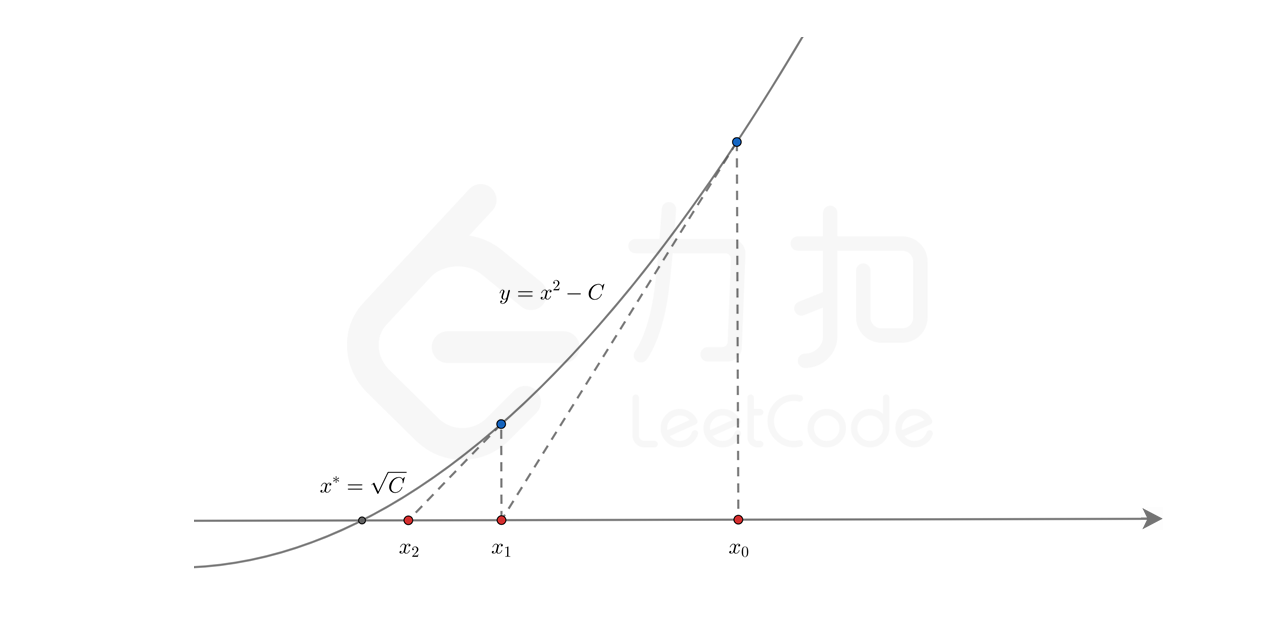
如图, 不断得用切线与X轴的交点为基础做切线迭代, 用于X轴的交点不断去逼近结果。
具体的公式推导如下:
我们选择 (x 0=C) 作为初始值。
在每一步迭代中, 我们通过当前的交点 (x_{i},) 找到函数图像上的点 (left(x_{i}, x_{2}^{2}-C
ight),) 作一条斜率为 (f^{prime}left(x_{i}
ight)=2 x_{i}) 的直线, 直线的方程为:
[egin{aligned}
y l &=2 x ileft(x-x_{i}
ight)+x_{2}^{2}-C \
&=2 x i x-left(x_{i}^{2}+C
ight)
end{aligned}
]
与横轴的交点为方程 (2 x i x-left(x_{2}^{2}+C ight)=0) 的解, 即为新的迭代结果 (x_{i+1}:)
[x_{i+1}=frac{1}{2}left(x_{i}+frac{C}{x_{i}}
ight)
]
在进行 (k) 次迭代后, (x_{k}) 的值与真实的零点 (sqrt{C}) 足田接近, 即可作为答案。
这种方法有几点需要明白:
为什么选择 (x 0=C) 作为初始值?
- 因为 (y=x^{2}-C) 有两个零点 (-sqrt{C}) 和 (sqrt{C}) 。如果我们取的初始值较小,可能会迭代到 (-sqrt{C}) 这 个零点, 而我们希望找到的是 (sqrt{C}) 这个零点。因此选择 (x 0=C) 作为初始值,每次迭代均有 (x_{i+1}<x_{i},) 零点 (sqrt{C}) 在其左侧, 所以我们一定会迭代到这个零点。
- 迭代到何时才算结束?
每一次迭代后, 我们都会距离零点更进一步,所以当相邻两次迭代得到的交点非常接近时, 我们 就可以断定, 此时的结果已经足够我们得到答案了。一般来说, 可以判断相邻两次迭代的结果的 差值是否小于一个极小的非负数 (epsilon,) 其中 (epsilon) 一般可以取 (10^{-6}) 或 (10^{-7}) 。 - 如何通过迭代得到的近似零点得出最终的答案?
由于 (y=f(x)) 在 ([sqrt{C},+infty]) 上是凸函数 (convex function) 且恒大于等于零,那么只要我们选取 的初始值 (x 0) 大于等于 (sqrt{C},) 每次迭代得到的结果 (x_{i}) 都会恒大于等于 (sqrt{C}) 。因此只要 (epsilon) 选择地足 句小, 最终的结果 (x k) 只会稍稍大于真正的零点 (sqrt{C}) 。在题目给出的 32 位整数范围内,不会出现 下面的情况:
真正的零点为 (n-1 / 2 epsilon,) 其中 (n) 是一个正整数, 而我们迭代得到的结果为 (n+1 / 2 epsilon_{circ}) 在对结 果保留整数部分后得到 (n,) 但正确的结果为 (n-1_{0})
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (Math.abs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return (int) x0;
}