本文主要有以下三部分内容:
- 介绍了Golomb编码,及其两个变种:Golomb-Rice和Exp-Golomb的基本原理
- C++实现了一个简单的BitStream库,能够方便在bit流和byte数字之间进行转换
- C++实现了Golomb-Rice和Exp-Golomb的编码,并进行了测试。
在文章的最后提供了本文中的源代码下载。
Golomb编码的基本原理
Golomb编码是一种无损的数据压缩方法,由数学家Solomon W.Golomb在1960年代发明。Golomb编码只能对非负整数进行编码,符号表中的符号出现的概率符合几何分布(Geometric Distribution)时,使用Golomb编码可以取得最优效果,也就是说Golomb编码比较适合小的数字比大的数字出现概率比较高的编码。它使用较短的码长编码较小的数字,较长的码长编码较大的数字。
Golomb编码是一种分组编码,需要一个正整数参数m,然后以m为单位对待编码的数字进行分组,如下图:

对于任一待编码的非负正整数N,Golomb编码将其分为两个部分:所在组的编号GroupID以及分组后余下的部分,GroupID实际是待编码数字N和参数m的商,余下的部分则是其商的余数,具体计算如下:
对于得到的组号q使用一元编码(Unary code),余下部分r则使用固定长度的二进制编码(binary encoding)。
一元编码(Unary coding)是一种简单的只能对非负整数进行编码的方法,对于任意非负整数num,它的一元编码就是num个1后面紧跟着一个0。例如:
| num | Unary coding |
|---|---|
| 0 | 0 |
| 1 | 10 |
| 2 | 110 |
| 3 | 1110 |
| 4 | 11110 |
| 5 | 111110 |
其编解码的伪代码如下:
UnaryEncode(n) {
while (n > 0) {
WriteBit(1);
n--;
}
WriteBit(0);
}
UnaryDecode() {
n = 0;
while (ReadBit(1) == 1) {
n++;
}
return n;
}使用一元编码编码组号也就是商q后,对于余下的部分r则有根据编码数字大小的不同有不同的处理方法。
- 如果参数m是2的次幂(这也是下面将要介绍的Golomb-Rice编码),则使用取r的二进制表示的低log2(m)log2(m)位,作为r的码字
- 如果参数m不是2的次幂,如果m不是2的次幂,设b=⌈log2(m)⌉b=⌈log2(m)⌉
- 如果r<2b−mr<2b−m,则使用b-1位的二进制编码r。
- 如果r≧2b−mr≧2b−m,则使用b位二进制对r+2b−mr+2b−m进行编码
总结,设待编码的非负整数为N,Golomb编码流程如下:
- 初始化正整数参数m
- 取得组号q以及余下部分r,计算公式为:q=N/m,r=N%mq=N/m,r=N%m
- 使用一元编码的方式编码q
- 使用二进制的方式编码r,r所使用位数的如下:
- 如果参数m是2的次幂(这也是下面将要介绍的Golomb-Rice编码),则使用取r的二进制表示的低log2(m)log2(m)位,作为r的码字。
- 如果参数m不是2的次幂,如果m不是2的次幂,设b=⌈log2(m)⌉b=⌈log2(m)⌉
- 如果r<2b−mr<2b−m,则使用b-1位的二进制编码r。
- 如果r≧2b−mr≧2b−m,则使用b位二进制对r+2b−mr+2b−m进行编码
说明:
- ⌈a⌉⌈a⌉ 大于a的最小整数 ceil运算
- ⌊a⌋⌊a⌋ 小于a的最大整数 floor运算
Golomb-Rice 编码
Golomb-Rice是Golomb编码的一个变种,它给Golomb编码的参数m添加了个限制条件:m必须是2的次幂。这样有两个好处:
- 不需要做模运算即可得到余数r,
r = N & (m - 1) - 对余数r编码更为简单,只需要取r二进制的低log2(m)log2(m)位即可。
则Golomb-Rice的编码过程更为简洁:
- 初始化参数m,m必须为2的次幂
- 计算q和r,
q = N / m ; r = N & (m - 1) - 使用一元编码编码q
- 取r的二进制位的低log2(m)log2(m)位作为r的码字。
解码过程如下:
bool b;
uint64_t unary = 0;
b = bitStream.getBit();
while (b)
{
unary++;
b = bitStream.getBit();
}
std::bitset<64> bits;
bits.reset();
for (int i = 0; i < k; i++)
{
b = bitStream.getBit();
bits.set(i, b);
}
N = unary * m + bits.to_ulong();Exponential Golomb 指数哥伦布编码
Rice的编码方式和Golomb的方法是大同小异的,只是选择m必须为2的次幂。而Exp-Golomb则有了一个很大的改进,不再使用固定大小的分组,而使组的大小呈指数增长。如下图:

Exp-Golomb的码元结构是:** [M zeros prefix] [1] [Offset] **,其中M是分组的编号GroupID,1可以看着是分隔符,Offset是组内的偏移量。
Exp-Golomb需要一个非负整数K作为参数,称之为K阶Exp-Golomb。其中当K = 0时,称为0阶Exp-Golomb,目前比较流行的H.264视频编码标准中使用的就是0阶的Exp-Golomb,并且可以将任意的阶数K转为0阶Exp-Golomb编码。
首先来看下0阶Exp-Golomb编码,如下图:
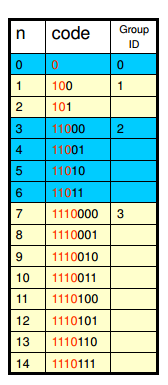
上图是0阶Exp-Golomb编码的前几个组的分组情况,可以看出编号为m的组,其组内的最小元素的值是2m−12m−1,也就是说对于非负整数N,其在编号为m的组内的充要条件是:2m−1≤N≤2m+1−12m−1≤N≤2m+1−1。所以可以由如下公式计算得到组号m以及组内的偏移量Offset
有了组号以及组内的偏移量后,其编码就比较简单了,具体过程如下:
- 首先使用公式计算组号m,m=⌊log2(num+1)⌋m=⌊log2(num+1)⌋
- 对组号m进行编码,连续写入m个0,最后写入一个1作为结束。
- 计算组内偏移量offset,Offset=num+1−2mOffset=num+1−2m
- 取offset二进制形式的低m位作为offset码元
0阶Exp-Golomb的编码后的长度是:2∗m+12∗m+1,其解码过程和上面的Rice码类似,读入bit流,是0则继续,1则停止,然后统计0的个数m;接着读入m位的bit,就是offset,最后解码后的数值是:N=2m−1+offsetN=2m−1+offset。
k阶Exp-Golomb
前面提到任意的k阶Exp-Golomb可以转换为0阶Exp-Golomb进行求解,这是为何呢。Exp-Golomb的组的大小实际上是呈2的指数增长,不同的参数k,实际控制的是起始分组的大小,具体是什么意思呢。
- k = 0,其组的大小为1,2,4,8,16,32,...
- k = 1,其组的大小为2,4,8,16,32,64,...
- k = 2,其组的大小为4,8,16,32,64,...
- ...
- k = n,其组的大小为2n,2n+1,⋯2n,2n+1,⋯
不同的k造成了其起始分组的大小不同,所以对于任意的k阶Exp-Golomb编码都可以转化为0阶,具体如下:
设待编码数字为N,参数为k
- 使用0阶Exp-Golomb编码 N+2k−1N+2k−1
- 从第一步的结果中删除掉高位的k个0
以上的算法描述来自: https://en.wikipedia.org/wiki/Exponential-Golomb_coding
在搜索得到中文资料中,对于K阶Exp-Golomb的算法描述大多如下:
- 将num以二进制的形式表示(若不足k位,则在高位补0),去掉其低k位(若刚好是k位,则为0)得到数字n
- 计算n + 1的最低有效位数lsb,则M = lsb - 1。就是prefix中0的个数
- 将第1步中去掉的k位二进制串放到(n + 1)的低位,得到[1][INFO]
其实现以及描述都不如wikipedia,故在下面的实现部分使用的是Wikipedia的方法。
在资料搜集的过程中,对于Exp-Golomb算法描述不止上述的两种,还有其他的形式,但都是殊途同归,也许得到的编码是不一样的,但是其编码的长度却是一样的,也就没有过多的计较。
最后附上k = 0,1,2,3时前29个数字的编码:
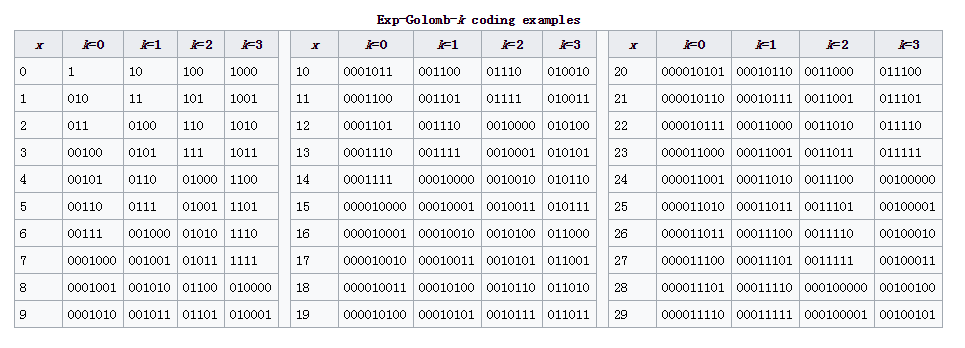
注意1之前的0的个数就是该数字所在的组的编号,同一组内的编码长度是相同的。
实现
通过上面的描述可以发现,Golomb编码的实现是很简单的,唯一的难点在于bit的操作。编码过程是将对bit进行操作,然后拼凑为byte,写入buffer;解码则是相反的过程,读取byte转化为bit stream,操作一个个的bit。具体来说就是以下两个功能:
- 将bit流转换为byte数组
- 将byte数组转换为bit流
而在C/C++中最小的数据类型也是8位的byte,这就造成了对bit的进行操作有一定的难度,好在C++中std::bitset结构能够在一定成都上简化对bit的操作。
BitBuffer / ByteBuffer
首先实现一个底层的库,实现bit流和byte之间的转换。在Golomb编码中,对bit和byte的操作只需要简单的get/put操作,因此封装了两个结构体BitBuffer和ByteBuffer,具体的声明如下:
//////////////////////////////////////////////////////
//
// Bits buffer
// 将bytes转化为bit stream时,在该buffer中缓存待处理的bit
//
/////////////////////////////////////////////////////
struct BitBuffer
{
std::bitset<bit_length> data; // 使用bitset缓存bit
int pos; // 当前bit的指针
int count;// bitset中bit的个数
// 构造函数
BitBuffer();
// 从bitset中取出一个bit
bool getBit();
// 从bitset中取出一个byte
uint8_t getByte();
// 向bitset中写入一个bit
void putBit(bool b);
// 向bitset中写入一个byte
void putByte(uint8_t b);
};
////////////////////////////////////////////////////
//
// Bytes buffer
//
///////////////////////////////////////////////////
struct ByteBuffer
{
uint8_t *data; // Byte数据指针
uint64_t pos; // 当期byte的指针
uint64_t length; // 数据长度
uint64_t totalLength; // 总的放入到 byte buffer中的字节数
// 构造函数
ByteBuffer();
// 取出一个byte
uint8_t getByte();
// 写入一个byte
void putByte(uint8_t b);
// 设置byte数组
void setData(uint8_t *buffer, int len);
};BitBuffer是一个bit的缓存,无论是将bit流转换为byte还是将byte转换为bit流,都将bit放在此结构体中进行缓存。ByteBuffer用来管理byte数组的缓存
这两个结构体中只向上层提供简单的get/put方法,不做任何的逻辑判断。也就是说只要调用了get方法就一定会有数据返回,调用了put方法就一定有空间存放数据。
BitStream
在编码时,需要将得到的bit流以byte的形式写出;解码则是将byte数组以bit流的形式读入。这就需要两种类型的bitstream:BitOutputStream和BitInputStream,其声明如下:
////////////////////////////////////////////////////////
//
// Bit Output Stream
// 将bit stream转化为byte数组
// 这里也只提供功能,至于byte缓存满的处理放到编码器中处理
//
////////////////////////////////////////////////////////
class BitOutputStream
{
;
public:
// 写入一个bit
void putBit(bool b);
// 写入多个相同的bit
void putBit(bool b, int num);
// 设置数据数组
void setBuffer(uint8_t *buffer, int len);
void resetBuffer();
/*
判断byte buffer中是可用的bit长度
*/
uint64_t freeLength();
// Flush bit buffer to byte buffer
bool flush();
uint64_t getTotalCodeLength()
{
return bytes.pos;
}
private:
BitBuffer bits;
ByteBuffer bytes;
};
class BitInputStream
{
public:
// 读取一个bit
bool getBit();
// 设置byte buffer
void setBuffer(uint8_t *buffer, int len);
BufferState check();
private:
BitBuffer bits;
ByteBuffer bytes;
};编码时需要BitOutputStream将bit流转换为byte数组,也就是个putBit的过程,需要注意的一点是在编码结束的时候需要调用方法flush,该函数有两个功能:
- 将BitBuffer中缓存的bit刷新到byte数组中
- 写入编码的编码终止符。编码终止符在解码过程中是一个很重要的判断标志,这里假定Golomb编码后码元的最大长度为64位,所以可设编码终止符为:连续64bits的0。在解码时,要判断接下来的是不是编码终止符。
- 将编码后输出的字节数填充为8(8 bytes,64 bits)的倍数,在解码时以8 bytes为单位进行解码,并且每次判断是不是编码终止符时也需要至少8 bytes。
编码/解码
有了BitStream的支持后,编解码过程是很简单的。
编码
每次编码前,首先计算编码后码元的长度,如果byte缓存空间不足以存放整个码元,则将byte buffer填充满后,剩余的部分,在bitset中缓存。返回false,指出缓存已满,需要处理缓存中的数据后才能继续编码或者更换一个新的Byte buffer存放编码后的数据.
bool GolombEncoder::encode(uint64_t num)
{
uint64_t q = num >> k;
uint64_t r = num & (m - 1);
auto len = q + 1 + k; // 编码后码元的长度
/*
不会判断缓存是否为满,直接向里面放,不足的话缓存到bit buffer中
*/
bitStream.putBit(1, q);
bitStream.putBit(0);
for (int i = 0; i < k; i++)
{
bitStream.putBit(static_cast<bool>(r & 0x01));
r >>= 1;
}
return bitStream.freeLength() >= len; // 空间足够,存放编码后的码元则返回true;否则返回false
}上述代码以Golomb-Rice编码为例。在putBit时候的不会判断缓存是否够用,直接存放,如果Byte Buffer不足以存放本次编码的bits,则将Byte Buferr填充满后,余下的bits在BitBuffer中缓存,然后返回false,告诉调用者byte buffer已经填满,可以处理当前buffer的数据后调用resetBuffer后继续编码;也可以直接更换一个新的byte buffer。
解码
在每次解码前,先要调用check方法来判断byte buffer的状态,byte buffer中有以下几种状态
- 空,数据已读取完
- 编码终止符,buffer中的数据是编码终止符,解码结束
- 数据不足,buffer中的数据不足以完成本次解码,需要读取新的buffer
- 数据足够,继续解码
check的实现如下:
enum BufferState
{
BUFFER_EMPTY, // buffer empty
BUFFER_END_SYMBOL, // end_symbol 编码的中止符,已经没有编码的数据
BUFFER_LACK, // buffer数据不足以完成解码,需要新的buffer
BUFFER_ENGOUGH // 数据足够,继续解码
};
// 检测buffer的状态
// 在每次解码开始前调用
BufferState BitInputStream::check()
{
// buffer中已无数据
if (bits.count <= 0 && bytes.pos >= bytes.length)
return BufferState::BUFFER_EMPTY;
// buffer中还有数据,分为两种情况:不足64bits和有64bits
auto count = (bytes.length - bytes.pos) * 8 + bits.count;
// buffer中的数据足够64位
if (count >= 64)
{
// bit buffer中数据就有64bits
if (bits.count >= 64)
{
if (bits.data.none()) // 64 bits 0
return BufferState::BUFFER_END_SYMBOL; // 编码中止符
else
return BufferState::BUFFER_ENGOUGH; // 数据足够继续解码
}
// bit buffer中的数据不足64bit
else
{
if (!bits.data.none())
return BufferState::BUFFER_ENGOUGH;
int count = ((64 - bits.count) / 8 + 1);
int index = 0;
while (index < count)
{
auto b = bytes.data[bytes.pos + index];
index++;
if (b != 0)
return BufferState::BUFFER_ENGOUGH;
}
return BUFFER_END_SYMBOL;
}
}
// buffer中数据不足64位,不进行解码,
// 将byte buffer中的数据取出放在bit buffer后,返回BUFFER_LACK
else
{
while (bytes.pos < bytes.length)
{
auto b = bytes.getByte();
bits.putByte(b);
}
return BufferState::BUFFER_LACK;
}
}check的过程有些复杂,但代码中的注释已足够清晰,这里就不再详述了。
Golomb-Rice的解码过程如下:
/////////////////////////////////////////////////////////
//
// 解码
// 在每次解码前需要check buffer的状态,根据不同的状态决定解码是否继续
//
///////////////////////////////////////////////////////
BufferState GolombDecoder::decode(uint64_t& num)
{
auto state = bitStream.check();
// buffer中数据足够,进行解码
if (state == BufferState::BUFFER_ENGOUGH)
{
bool b;
uint64_t unary = 0;
b = bitStream.getBit();
while (b)
{
unary++;
b = bitStream.getBit();
}
std::bitset<64> bits;
bits.reset();
for (int i = 0; i < k; i++)
{
b = bitStream.getBit();
bits.set(i, b);
}
num = unary * m + bits.to_ulong();
}
return state;
}解码完成后会返回当前byte buffer的状态,
- 状态是
BUFFER_END_SYMBOL,则解码过程已经完成 - 状态是
BUFFER_EMPTY,byte buffer没有设置 - 状态是
BUFFER_LACK,byte buffer中的数据不足以完成一次解码,需要读入新的数据 - 状态是
BUFFER_ENGOUGH,byte buffer中的数据足够,继续下一次的解码
测试
仍然以Golomb-Rice编码为例,测试代码如下
GolombEncoder encoder(m);
encoder.setBuffer(buffer, 1024);
ofstream ofs;
ofs.open("golomb.gl", ios::binary);
for (int i = 0; i < length; i++)
{
auto b = encoder.encode(nums[i]);
if (!b)
{
cout << "Lack of buffer space,write the data to file" << endl;
cout << "reset buffer" << endl;
ofs.write((const char*)buffer, encoder.getToalCodeLength());
encoder.resetBuffer();
break;
}
}
encoder.close();
ofs.write((const char*)buffer, encoder.getToalCodeLength());
ofs.close();
cout << "Golomb finished coding" << endl;- 实例编码器时,需要设定编码的参数m和以及存放编码后数据的buffer;
- 编码时,判断编码的的返回值,如果为true则继续编码,为false则buffer已满,将buffer写入文件后,
resetBuffer继续编码。 - 编码结束后,调用
close方法,写入编码终止符,并将整个编码后的数据填充为8的倍数。
下面代码Golomb-Rice的解码调用过程
ifstream ifs;
ifs.open("golomb.gl", ios::binary);
memset(buffer, 0, 1024);
ifs.read((char*)buffer, 664);
ofstream encodeOfs;
encodeOfs.open("encode.txt");
GolombDecoder decoder(m);
decoder.setBuffer(buffer, 1024);
uint64_t num;
auto state = decoder.decode(num);
int index = 0;
while (state != BufferState::BUFFER_END_SYMBOL)
{
encodeOfs << num << endl;
state = decoder.decode(num);
index++;
}
ifs.close();
encodeOfs.close();
cout << "decode finished" << endl;编码是也需要根据返回的状态,来处理byte buffer,在上面已详述。
总结
终于完成了这篇博文,本文主要对Golomb编码进行了一个比较详尽的描述,包括Golomb编码的两个变种:Golomb-Rice和Exp-Golomb。在编码实现部分,难点有三个:
- byte数组和bit流之间的转换
- 需要一个唯一的编码终止符
- 解码时,byte buffer中剩余数据不足以完成一次解码
针对上述问题,做了如下工作:
- 实现了一个简单的BitStream库,能够方便在bit流和byte数组之间进行转换
- 对编码后的码元长度做了一个假设,其最长长度不会超过64位,这样就使用64比特的0作为编码的终止符
- 在编码的时,会将编码后的总字节数填充为8的倍数,解码的过程中就以8字节为单位进行,当byte buffer中的数据不足8字节时,可以判定当前buffer中的数据并不是全部的数据,需要继续读入数据已完成解码