Network
之前将人工神经网络的 BP算法给详细推导了2遍, 算是对神经网络有了一个初步的认识, 当然, 重点还是算法的推导, 从数学的角度看, 就是多元复合函数求偏导, 应用链式法则 而已, 思想非常朴素.
而神经网络初步认识来看, 跟传统的 ML 理论的区别在于, 它更像一个经验的过程, 即debug. 它将一个样本输入(向量) 的每个分量, 进行一些 奇怪 的线性处理 (加权, 求和), 然后进行压缩投影 (0-1), 这样一层层地处理数据, 最后再来个 归一化 为一个向量(近似概率) 的输出. 这个过程呢, 称为 前向, 得到结果跟真实值之间的误差, 通过 反向 传递的方式来 动态调整权值参数 直到每个节点的 梯度接近0 就停止了调整了, 也就意味着, 网络基本构建完成了.
很多人都总是从生物学的角度来看待神经网络, 对我这种典型的文科生而已, 这反而增加了理解的难度, 什么神经元, 突触, 网络这些... 很害怕. 但我从控制论 的角度来理解, 神经网络过程, 其实就是一个 正反馈, 和 负反馈 的过程. 我突然想举个小栗子.
我小的时候在乡下, 家里的电视是需要安装一个很大的那种 "天锅" 来接收卫星信号的. 锅很大, 在老家的一个院子里, 用一个木的柱子给支起来, 一刮风, 就容易没信号, 尤其是正在看动画片来劲的时候给断信号. 处理方式呢, 就是去手动给挪动 "锅" 的位置, 另一个小伙伴盯着电视, 一边给我反馈, 有还是没有. 往左挪动还是往右, 这样一点点的调试, 知道有信号为止. 稍带回忆了一波童年. 通过调试, 能够看到调试结果和预期直接的 偏差 , 这个过程就是 前向 呀, 而根据 偏差 我知道下一步要如改进调整的方向和力度, 这个就是 误差反向传递的过程呀, 即负反馈 嘛. 从生活中来理解, 我觉得是让理论落地的最快办法.
还有一个更直观的栗子, 考驾照时, 科目二的 倒车入库 这个不断调试的过程就是 负反馈过程呀.
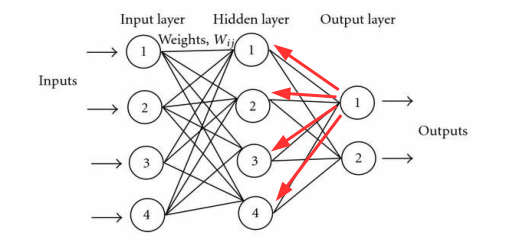
最后我从数据角度来理解, 感觉神经网络更像是一个 数据处理, 数据建模的过程 , 我有一个目标, 就是达到老板期望的预测值, 但我的数据如果不处理, 不做特征工程是不行的, 但是又没有经规范化的方法 让我选择哪些特征, 于是呢, 我只能 凭借专业理论知识, 业务知识, 随机瞎弄 进行不断试验, 每次都进行这些参数的记录, 一旦发现达到老板的期望值, 就把这些参数给记录下来, 这就是经验. 但有个问题, 中间的过程可能很复杂和有点黑箱, 这就引出一个更致命的问题 模型的可解释性低, 这也是我个人几乎不怎么用神经网络的原因. 因为我可能很难像老板解释, 为甚么会这样.
但凡学过商科, 学过经济的小伙伴都清楚, 参数的可解释性, 绝对是最为重要的, 没有之一. 那我为啥又要来整一下神经网络呢, 好奇呀.
为啥又要来整卷积呢, 这个词更为奇怪. 之前有讨论过, 从学界来看, 一个3层的网络结构, 只要中间节点够多, 几乎可以模拟世界上所有的函数. 而卷积呢, 相对于是增加了网络的层数, 为啥要这样做... 看完这篇笔记就明白了.
卷积的原理
卷积神经网络, 常见的应用场景, 如在自然语言处理方面, 对文章进行分类等. 或者在强化学习中, 如让机器自动学会聊天, 下棋等. 但最为直观的, 还是在 计算机视觉方面, 典型的图像识别来阐明卷积神经网络是最好的啦.
卷积神经网络 (Convolutional Neuron Networks) 简称 CNN . 最早提出来是 1998 年被4个大神在Patper中提出的. 是谁咱也不想问, 咱也不知道. 当时想解决就是想解决一个 图片识别的问题. 输入呢是手写数字图片, 通过多个卷积层以后呢, 产生一个分类的问题, 输出是一个 1~10 的数字, 类似于一个 概率分布.
图片的数字表达
以一个灰度的图像为例, 要将图片数字化表达, 即是一个二维的矩阵. 黑和白的颜色强度呢, 可用用数字 (0 -255) 来表达, 越接近 0 就越黑呀. 最白就是255呀. 为啥是 0-255, 计算机中一般用 8 bit 来存储一个颜色的值. 那能存最大的值不就是 ((1 1 1 1 1 1 1 1)_2 = 255) 再加上 0, 一个256个色阶.

卷积 Convolution
就是一种变换而已, 对输入矩阵的值进行 某种变换, 产生一个同样大的 新矩阵. 暂时也不知道怎么解释好, 感觉人家就是这么玩的.
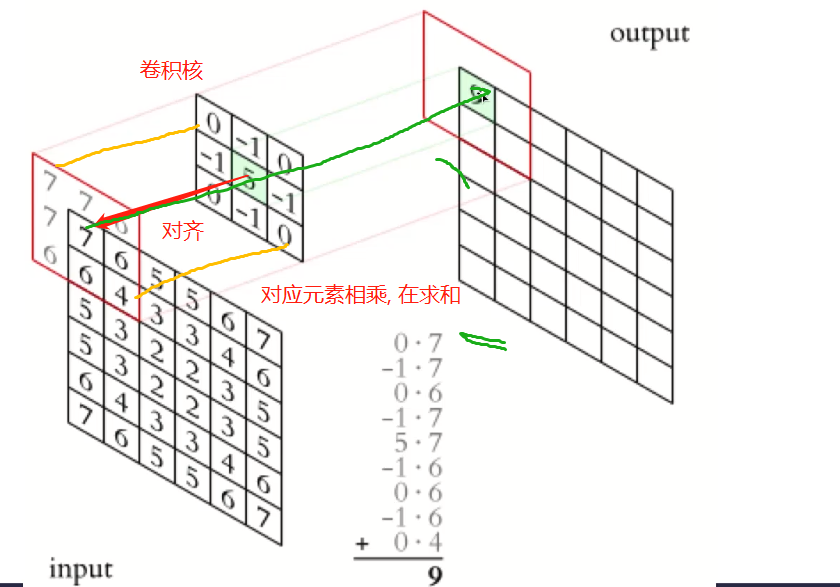
再求和, 打错字了. 不想改了, 意思到了就行.
然后, 再移动一下, 将卷积核 的中心 5 对准 输入矩阵的第二个元素 6, 做同样的操作. 对应元素相乘, 再求和. 将结果填充到输出矩阵的的对应位置 (a_{12}).
.... 就一直这样, 用 卷积核来 "扫描" 输入矩阵的每个元素, 并填充到对应 输出矩阵的对应位置...
卷积核: 核 (kernel) 的概念, 跟前面 svm 的 kernel 是类似的, 嗯, 就可理解为 某种算子(option) 吧.
缺失值: 如上示意图, 假设有缺失, 则可进行 填充, 方式有很多, 如 knn呀, 均值呀之类的, 自己看着办.
维数: 输入是 nxp 的矩阵, 输出也是 nxp的矩阵. 维数没有变化, 只是数据经过 kernel 给改变了.
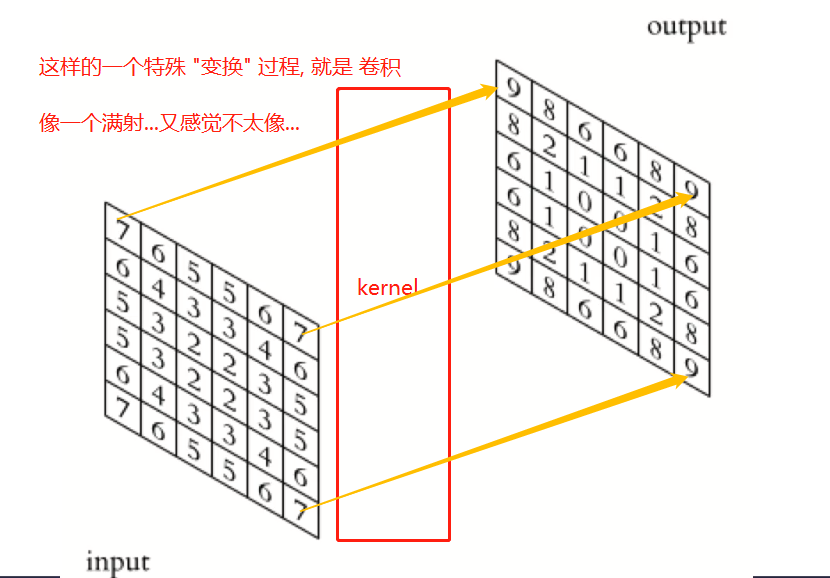
卷积 (convolution) 大致就是这样的一个 变换过程, 目测应该是线性的, 因为其只是涉及 加法和数乘 , 但其变换的 矩阵, 暂时我感觉写不出来呀...., anyway, 卷积这个概念, 应该是有初步的理解了.
最大池化 Max Pool
卷积可以看作是对输入矩阵的一个变换(通过卷积核), 得到一个新的矩阵, 数值改变了, 但维数是没有变的, 于是一般会进行一个池化的操作, 对于新矩阵. 即把矩阵进行 降维, 比如卷积后的矩阵是 4 x 4 的, 通过 池化呢, 变为了 2x2 的. 但这个降维 跟前面的 PCA 和 LDA 不同, 没有那么麻烦, 需要计算方差, 投影什么的. 池化, 就是大致是将, 矩阵进行一个 过滤, 分块 操作, 每一块用 一个值来代表该区域的特征.
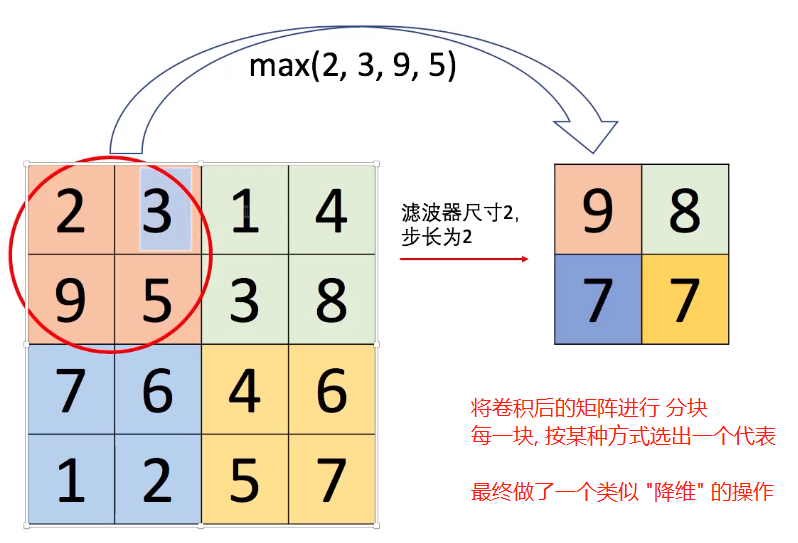
不对, 纠正一下, 不是 分块, 因其有 尺寸 和步长 的概念嘛, 更像是一个不断过滤 的过程, 因此叫滤波器嘛 , 不改图了, 适当给自己留点退路.
平均池化 Average Pool
跟最大池化,的唯一区别在于, 每次过滤出来而 "小块" 中的 代表值的计算方式不同而已, 最大池化是选小块中最大的数字, 而平均池化自然是选择最该小区域的平均值了呀.
卷积作为特征提取器
卷积和池化的作用呢, 从效果上来看, 就类似一个, 提取图片主要特征的过程.
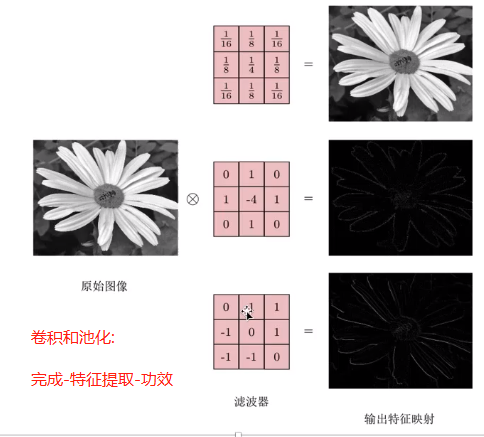
感觉这应该是卷积最大的功效了. 提取图片的主要特征. 至于用什么样的 滤波器, 卷积核, 以及如何选择池化的方式, 这是一个, 调参 的过程, 没有严格的理论证明和推导. 有些经验是说, 选择用大量较小的核 和 更多的层数 来进行选择. 这些传统的核的选择, 也是前人的一些经验的结果, 有点像个黑箱操作, 经验值等. 多测试验证似乎只能这样.
典型的 CNN 网络结构
黑白图像
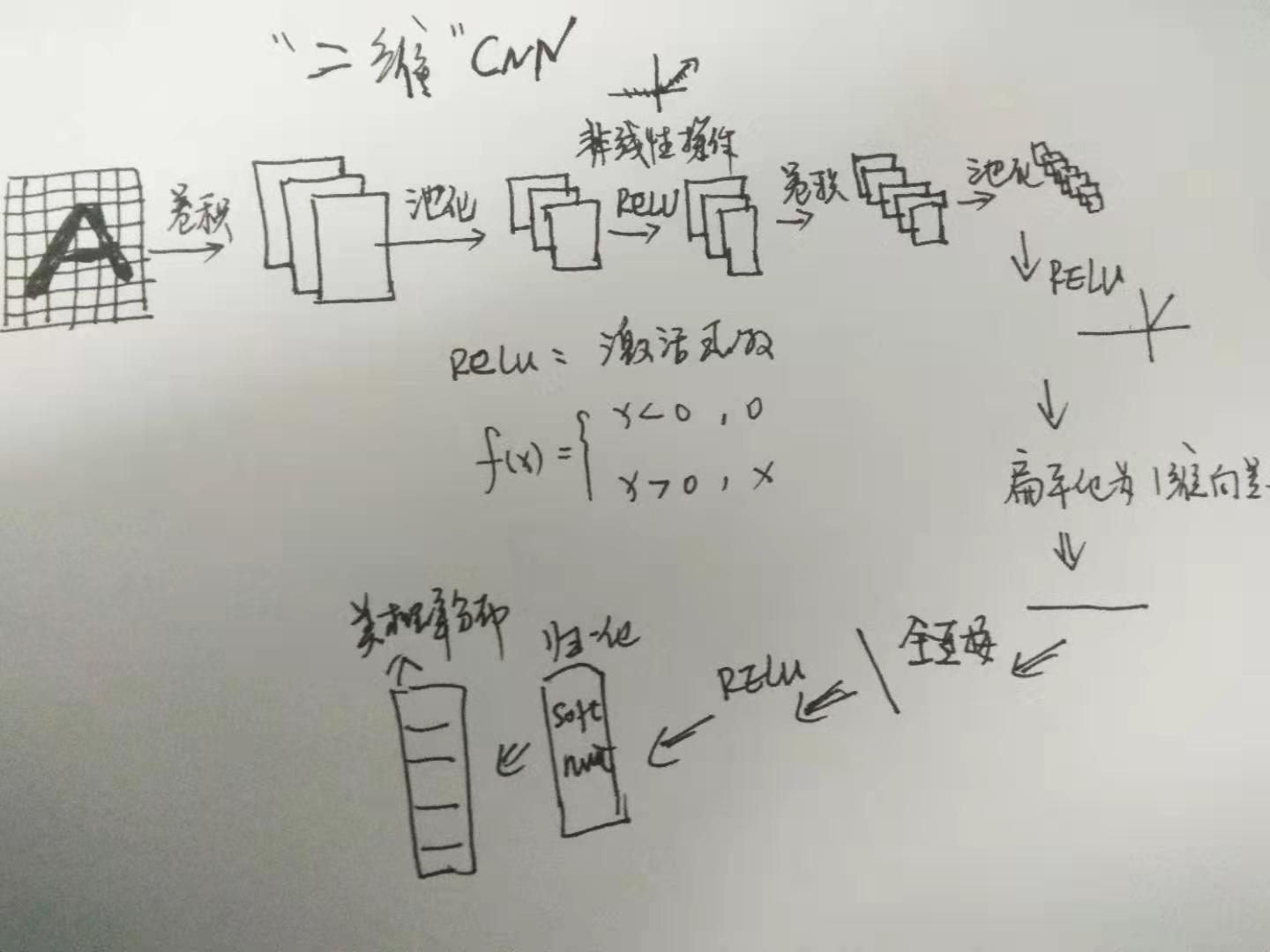
彩色图像
单个矩阵是表达不能表达了, 用 RGB 这样的3个矩阵来表达呀, 分别是 R, G, B 三个矩阵, 同时呢, 也可以选择多个不同的核和滤波器来进行选择.

还可以, 这波彩色图片的操作. 也没啥特别的, 就是这么做的呀.
Why Convolution
卷积层的特征
上面说到了, 卷积的过程可以看作是一个特征提取的过程. 那为什么要进行卷积操作呢? 或者说, 能进行特征提取的依据是什么?
其实, 原因非常直观, 卷积能提取特征, 是 利用了图像的局部像素间的相关性(locality). 就是像素之间的关系呀.
带来的好处是显而易见的, 降低了网络系数的数量(模型的复杂度), 避免过拟合 , 做了卷积和过滤嘛, 肯定是大幅度降低了计算复杂度, 尤其是节约了内存.
至于过拟合这个点, 之前的各种 ML 算法几乎都讨论通透了. 模型越复杂, 就越容易过拟合. 正好插又插一嘴, 在接触 ML之前呢, 我的所有数据分析, 建模理论, 都是 统计建模. 包括在学术上也是, 我一直在尽可能地让模型去几乎能去模拟样本数据 即一直走在过拟合的路上. 模型太复杂, 很多时候反而不好.
降低计算复杂度
假设呢, 我们有输入一个 200x200 的黑白图片.
**首先考虑全连接层. **
对于普通全连接层, 层数不多, 但隐含层的节点非常多( 要拟合嘛), 隐含层神经元大于输入层个数., 在做向量拉伸(flat) 的时候, 200x200 = 4000 这是输出节点个数. 然后假设隐藏神经元为 60000. 则第一个隐含层包含的系数个数:
((200 * 200 + 1) * 60000 = 2400060000)
假设一个浮点数存储占 4个byte, 则需要的空间为: (2400060000 * 4/ (1024^3) = 8.9GB)
我的天哪, 就处理个 200x200 的图片要用 8.9GB 的空间, 这也太扯了..
然后考虑卷积层
假设有 20 个滤波器, 每个尺寸为 5x5, 则第一个卷积层包含的系数个数为:
((5 * 5 + 1) * 20 = 520)
需要的内存为: ((520 * 4) / (1024^3) = 2k)
这二者简直是指数级 的差异哦, 在空间占用这一方面上.
小结
本篇的目的, 就是对卷积 CNN 有一个直观上的认识, 重点在理解概念即可.
- 卷积的概念和应用场景
- 卷积和池化过程 (卷积, 卷积核, 滤波器, 步长...)
- 卷积带来的好处, 提取图片主要特征, 降低计算量, 尤其是在空间上.