可怜的小猪&香农熵

这是一道leetcode上面的题：https://leetcode-cn.com/problems/poor-pigs/

 开始看到真的一头雾水，看了很多题解。最后恍然大悟只要明白进制这题也就不难了。

下面以示例1参考：从1000个桶bucket中找到其中一桶有毒的，问在规定的时间内最少需要几头猪？

桶状态bucket有且只有两种：无毒1、有毒0。

猪的状态state有且只有两种：存活1、死亡0。

有 bucket0 <--> state0　　&　　bucket1 <--> state1

------做一次实验试出毒药，找出1000桶bucket的毒药至少需要多少只猪呢？-------

H(X) = log₂1000 = 9.96　　10头　　

这也是香农熵的公式。

1000桶按二进制（0/1）编码。每头猪给喂当前当前进制位上为1的桶的所有液体，如猪1喂（1,3,5,7.....），猪2喂（2,3,6,7,10....）。

假设第666桶bucket是有毒的。

那么结果必然是只有（1,3,6,7,9）号猪是活的，（2,4,5,8,10）号猪死了。那么猪死了就把对应的二进制位置为1，二进制转换1010011010 --------- 666。所以666桶有毒。

--------------那么可以做4次试验，找出1000桶bucket的毒药至少需要多少只猪呢？-------------

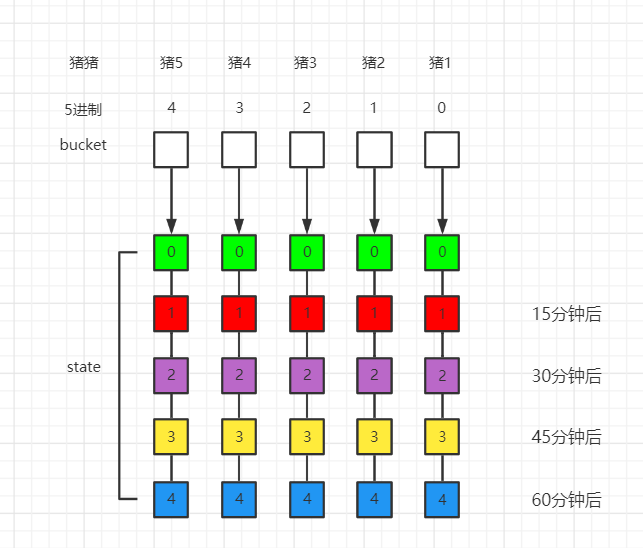
1、依然是把1000个桶bucket按照5进制分组；此时只需要5bit的信息。

2、每头猪给喂当前进制位上为1的桶的所有液体（0-15分钟），当前进制位上为2的桶的所有液体（15-30分钟），当前进制位上为3的桶的所有液体（30-45分钟），当前进制位上为4的桶的所有液体（45-60分钟）。

3、那么一只猪有5种状态，15分钟死亡（state1），30分钟死亡（state2），45分钟死亡（state3），60分钟死亡（state4），最终存活（state0）；

H(X) = log₅1000 = 4.29　　5头

最好的情况，5进制转换 11111 ------- 781,第一次试验就知道了781只桶有毒。

同样假设第666桶有毒，那么结果必然是（1号、3号、5号）猪1轮亡，2号猪3轮亡，4号猪经过四轮后存活。5进制转换10131 ------ 666 ，结果是666号桶有毒。

理解了这个编码就变得非常简单了

class Solution {
        public int poorPigs(int buckets, int minutesToDie, int minutesToTest) {
            int state = minutesToTest / minutesToDie + 1;
            return (int)Math.ceil(Math.log(buckets)/Math.log(state));
        }
    }

这里试验次数+1，才是state的状态。最后一种状态可以在前面结果全部取反时，直接得到。

方案是没问题的，至于为什么这样做是最优的。香农大佬早已经给出了答案，任何想逾越这个极限去解决问题的人最后都会被证明是徒劳的。

公式简单，但其背后关于进制的转换以及所蕴含的信息论知识是值得思考的。

 

参考：

https://www.zhihu.com/question/60227816/answer/1274071217

https://leetcode-cn.com/problems/poor-pigs/solution/xiao-song-man-bu-dai-ma-bu-zhong-yao-xue-poet/

https://leetcode-cn.com/problems/poor-pigs/