一、几种排序的比较:

二、排序的代码实现
1、冒泡排序
给定一组随机数字的数列,将它们按照从小到大的顺序重新排列好。就像冒泡一样,小的数不断地向上漂浮,直到没有为止。
排序基本思路:循环这个数列,将循环到的数字n1与下一个数字n2作出对比,如果n2>n1,那么将两个值换位,如此下去当第一次循环结束时,最小的数已经在最前面,重复这样的循环就会将这组数按从小到大的顺序排列好。
li = [11,432,5,4576,234,3,324,5,876,456,235432,56]
for m in range(len(li)-1):
for n in range(m+1, len(li)):
if li[m] > li[n]:
tmp = li[m]
li[m] = li[n]
li[n] = tmp
print li
测试排列5万个小于2000的随机数字,结果发现用时为:118秒
2、选择排序
与冒泡排序类似,循环整个数组,将数组中的值与第一个数值做对比,并将较小的值放在第一位。第一次循环就可以找出最小的一个值,以此类推下去,知道全部排列好。
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import random,time
def selection_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]:
tmp = array[i]
array[i] = array[j]
array[j] = tmp
if __name__ == '__main__':
# array = [871,100,160,755,614,621,403,671,256,915,174,906]
array = []
for i in range(50000):
array.append(random.randrange(100000))
time_start = time.time()
selection_sort(array)
time_end = time.time()
ret = time_end-time_start
print array
print(ret)
测试排列5万个小于2000的随机数字,结果发现用时为:115秒
选择排序的优化
当我们在循环中,判断出后面的值与第一个值的大小,那么先不做出交换,仅仅记录下这个较小值的下标。当第一次循环完时才把最小值放置在最前面,这样交换的次数更少了,速度就更快乐了。
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import random,time
def selection_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]:
tmp = array[i]
array[i] = array[j]
array[j] = tmp
if __name__ == '__main__':
# array = [871,100,160,755,614,621,403,671,256,915,174,906]
array = []
for i in range(50000):
array.append(random.randrange(2000))
time_start = time.time()
selection_sort(array)
time_end = time.time()
ret = time_end-time_start
# print array
print(ret)
测试排列5万个小于2000的随机数字,结果发现用时为:105秒
3、插入排序(Insertion Sort)
排序基本思路:插入排序简单的理解为 从一组数据的第二个值n开始循环,通过n与前面数值对比大小,将n插入到前面合适的位置。通过不断地向后循环对比大小,那么前面一部分的数据始终是已经排序好的数组。这样全部循环下来,就得到了一个从小到大排列OK的数组。
[77, 92, 67, 8, 6, 84, 55, 85, 43, 67]
[67, 77, 92, 8, 6, 84, 55, 85, 43, 67]
[8, 67, 77, 92, 6, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 92, 84, 55, 85, 43, 67]
[6, 8, 67, 77, 84, 92, 55, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 92, 85, 43, 67]
[6, 8, 55, 67, 77, 84, 85, 92, 43, 67]
[6, 8, 43, 55, 67, 77, 84, 85, 92, 67]
[6, 8, 43, 55, 67, 67, 77, 84, 85, 92]

# _*_coding:utf:8_*_
import random
import time
def sort_meth(source):
for i in range(1, len(source)):
currant_val = source[i] # 获取当前循环列表中的值
position = i # 获取当前循环的次数
while position > 0 and source[position-1] > currant_val: # 当左边的数大于大循环中的数时
source[position] = source[position-1] # 将小循环此刻的数赋值等于左边较大的值
position -= 1
source[position] = currant_val # 最终小循环结束时,就是大循环的数应该插入的位置
if __name__ == '__main__':
#array = [871,100,160,755,614,621,403,671,256,915,174,906]
array = []
for i in range(50000):
array.append(random.randrange(2000))
time_start = time.time()
sort_meth(array)
time_end = time.time()
ret = time_end-time_start
print(ret)
测试排列5万个小于2000的随机数字,结果发现用时为:115秒
4、快速排序(quick sort)
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动
注:在待排序的文件中,若存在多个关键字相同的记录,经过排序后这些具有相同关键字的记录之间的相对次序保持不变,该排序方法是稳定的;若具有相同关键字的记录之间的相对次序发生改变,则称这种排序方法是不稳定的。
要注意的是,排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中,只要有一个实例使得算法不满足稳定性要求,则该排序算法就是不稳定的。
排序演示
|
下标
|
0
|
1
|
2
|
3
|
4
|
5
|
|
数据
|
6
|
2
|
7
|
3
|
8
|
9
|
|
下标
|
0
|
1
|
2
|
3 |
4
|
5
|
|
数据
|
3
|
2
|
7
|
6
|
8
|
9
|
|
下标
|
0
|
1
|
2
|
3
|
4
|
5
|
|
数据
|
3
|
2
|
6
|
7
|
8
|
9
|
|
下标
|
0
|
1
|
2
|
3
|
4
|
5
|
|
数据
|
3
|
2
|
6
|
7
|
8
|
9
|
# _*_coding:utf-8_*_
import random
import time
def quick_sort(array, start, end):
if start >= end:
return
left = start
right = end
value = array[left]
while left < right:
while left < right and array[right] > value:
right -= 1
array[left] = array[right]
array[right] = value
while left < right and array[left] <= value:
left += 1
array[right] = array[left]
array[left] = value
quick_sort(array, start, left-1)
quick_sort(array, left+1, end)
if __name__ == '__main__':
# array = [871,100,160,755,614,621,403,671,256,915,174,906]
array = []
for i in range(50000):
array.append(random.randrange(2000))
time_start = time.time()
quick_sort(array, 0, len(array)-1)
time_end = time.time()
ret = time_end-time_start
print(ret)
测试排列5万个小于2000的随机数字,结果发现用时为:0.233秒,
当看到这个结果,其实我是惊呆了!
5、二叉树
树的特征和定义
树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样。树结构在客观世界中广泛存在,如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用,如在编译源程序时,可用树表示源程序的语法结构。又如在数据库系统中,树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。
树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树:
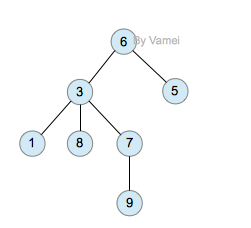
树有多个节点(node),用以储存元素。某些节点之间存在一定的关系,用连线表示,连线称为边(edge)。边的上端节点称为父节点,下端称为子节点。树像是一个不断分叉的树根。
每个节点可以有多个子节点(children),而该节点是相应子节点的父节点(parent)。比如说,3,5是6的子节点,6是3,5的父节点;1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点,称为根节点(root),如图中的6。没有子节点的节点称为叶节点(leaf),比如图中的1,8,9,5节点。从图中还可以看到,上面的树总共有4个层次,6位于第一层,9位于第四层。树中节点的最大层次被称为深度。也就是说,该树的深度(depth)为4。
如果我们从节点3开始向下看,而忽略其它部分。那么我们看到的是一个以节点3为根节点的树:
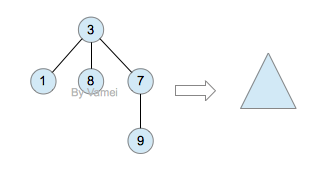
三角形代表一棵树
再进一步,如果我们定义孤立的一个节点也是一棵树的话,原来的树就可以表示为根节点和子树(subtree)的关系:
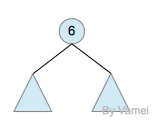
上述观察实际上给了我们一种严格的定义树的方法:
1. 树是元素的集合。
2. 该集合可以为空。这时树中没有元素,我们称树为空树 (empty tree)。
3. 如果该集合不为空,那么该集合有一个根节点,以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。
上面的第三点是以递归的方式来定义树,也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征,许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。
树的实现
树的示意图已经给出了树的一种内存实现方式: 每个节点储存元素和多个指向子节点的指针。然而,子节点数目是不确定的。一个父节点可能有大量的子节点,而另一个父节点可能只有一个子节点,而树的增删节点操作会让子节点的数目发生进一步的变化。这种不确定性就可能带来大量的内存相关操作,并且容易造成内存的浪费。
一种经典的实现方式如下:
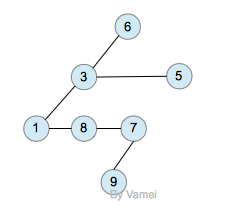
树的内存实现
拥有同一父节点的两个节点互为兄弟节点(sibling)。上图的实现方式中,每个节点包含有一个指针指向第一个子节点,并有另一个指针指向它的下一个兄弟节点。这样,我们就可以用统一的、确定的结构来表示每个节点。
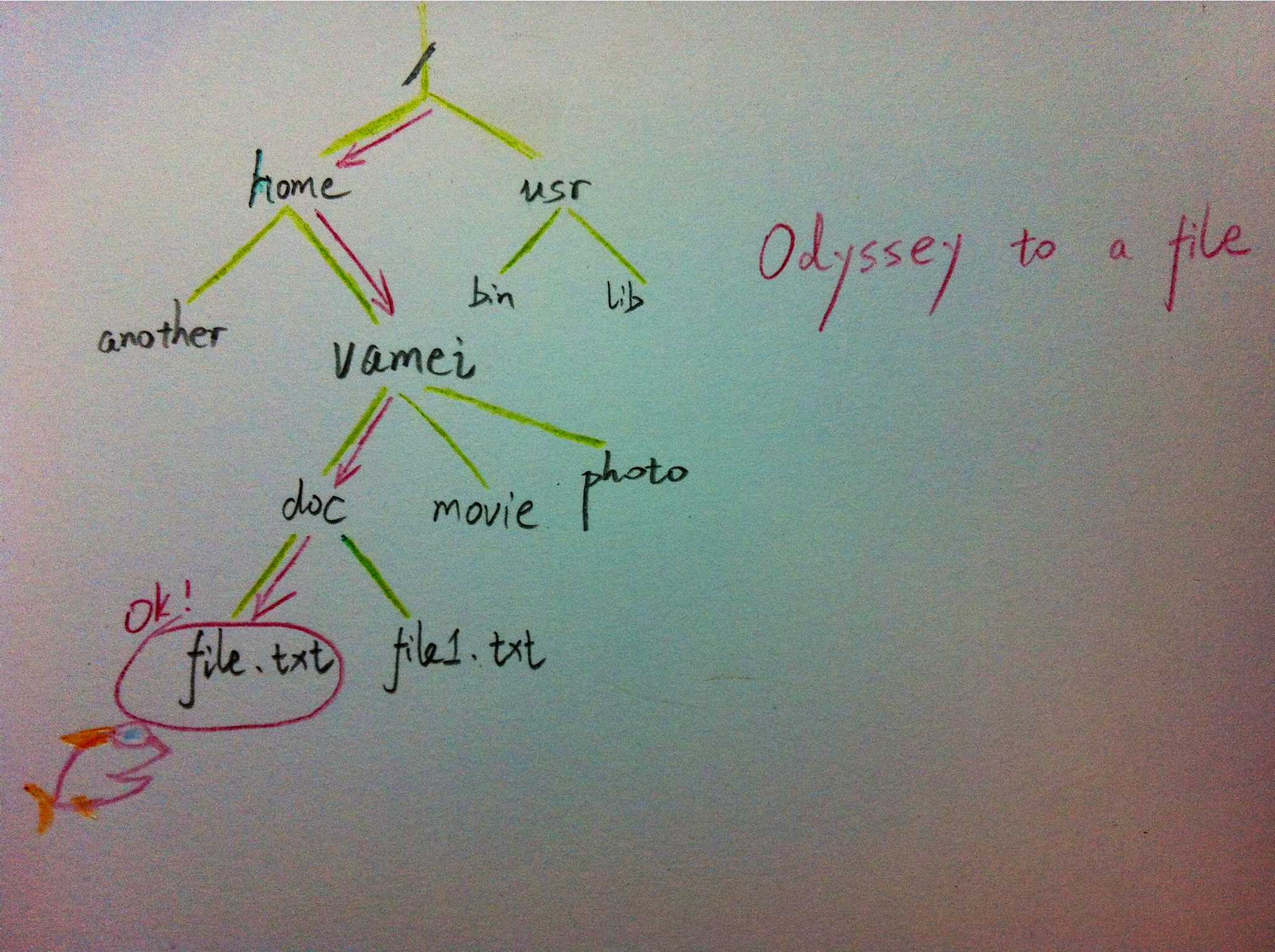
计算机的文件系统是树的结构,比如Linux文件管理背景知识中所介绍的。在UNIX的文件系统中,每个文件(文件夹同样是一种文件),都可以看做是一个节点。非文件夹的文件被储存在叶节点。文件夹中有指向父节点和子节点的指针(在UNIX中,文件夹还包含一个指向自身的指针,这与我们上面见到的树有所区别)。在git中,也有类似的树状结构,用以表达整个文件系统的版本变化 (参考版本管理三国志)。
二叉树
二叉树是由n(n≥0)个结点组成的有限集合、每个结点最多有两个子树的有序树。它或者是空集,或者是由一个根和称为左、右子树的两个不相交的二叉树组成。
特点:
(1)二叉树是有序树,即使只有一个子树,也必须区分左、右子树;
(2)二叉树的每个结点的度不能大于2,只能取0、1、2三者之一;
(3)二叉树中所有结点的形态有5种:空结点、无左右子树的结点、只有左子树的结点、只有右子树的结点和具有左右子树的结点。

二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点:
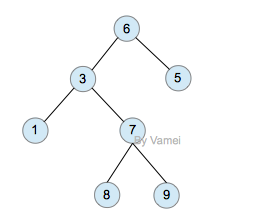
二叉树
由于二叉树的子节点数目确定,所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点,右子节点是右子树的根节点。
如果我们给二叉树加一个额外的条件,就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求:每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大。
(如果我们假设树中没有重复的元素,那么上述要求可以写成:每个节点比它左子树的任意节点大,而且比它右子树的任意节点小)
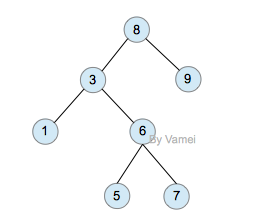
二叉搜索树,注意树中元素的大小
二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候,我们可以将x和根节点比较:
1. 如果x等于根节点,那么找到x,停止搜索 (终止条件)
2. 如果x小于根节点,那么搜索左子树
3. 如果x大于根节点,那么搜索右子树
二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n,最少为log(n)。
二叉树的遍历
遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历,中序遍历,后序遍历。
前序遍历:根节点->左子树->右子树
中序遍历:左子树->根节点->右子树
后序遍历:左子树->右子树->根节点
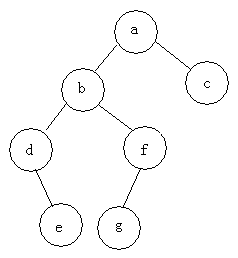
例如:求下面树的三种遍历
前序遍历:abdefgc
中序遍历:debgfac
后序遍历:edgfbca
二叉树的类型
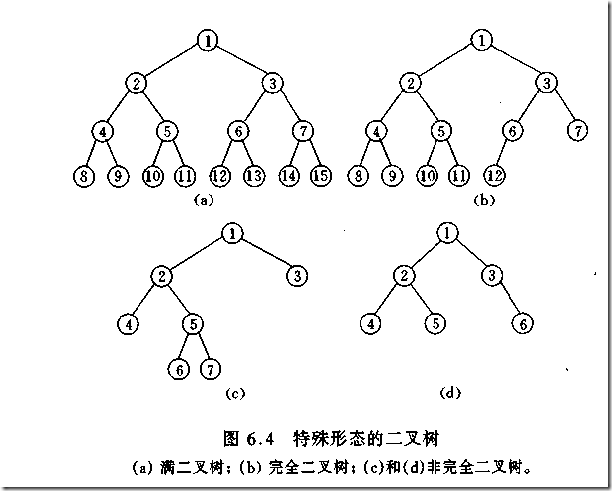
如何判断一棵树是完全二叉树?按照定义,
教材上的说法:一个深度为k,节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解,
就是一棵树,深度为k,并且没有空位。
首先对满二叉树按照广度优先遍历(从左到右)的顺序进行编号。
一颗深度为k二叉树,有n个节点,然后,也对这棵树进行编号,如果所有的编号都和满二叉树对应,那么这棵树是完全二叉树。
如何判断平衡二叉树?
二叉树遍历实现

class TreeNode(object): def __init__(self,data=0,left=0,right=0): self.data = data self.left = left self.right = right class BTree(object): def __init__(self,root=0): self.root = root def preOrder(self,treenode): if treenode is 0: return print(treenode.data) self.preOrder(treenode.left) self.preOrder(treenode.right) def inOrder(self,treenode): if treenode is 0: return self.inOrder(treenode.left) print(treenode.data) self.inOrder(treenode.right) def postOrder(self,treenode): if treenode is 0: return self.postOrder(treenode.left) self.postOrder(treenode.right) print(treenode.data) if __name__ == '__main__': n1 = TreeNode(data=1) n2 = TreeNode(2,n1,0) n3 = TreeNode(3) n4 = TreeNode(4) n5 = TreeNode(5,n3,n4) n6 = TreeNode(6,n2,n5) n7 = TreeNode(7,n6,0) n8 = TreeNode(8) root = TreeNode('root',n7,n8) bt = BTree(root) print("preOrder".center(50,'-')) print(bt.preOrder(bt.root)) print("inOrder".center(50,'-')) print (bt.inOrder(bt.root)) print("postOrder".center(50,'-')) print (bt.postOrder(bt.root))