介绍一个EM算法的应用例子:高斯混合模型参数估计。
高斯混合模型
高斯混合模型(Gaussian Mixture Model, GMM)是由多个高斯分布组成的模型,其密度函数为多个高斯密度函数的加权组合。
这里考虑一维的情况。假设样本 x是从 K 个高斯分布中生成的。每个高斯分布为
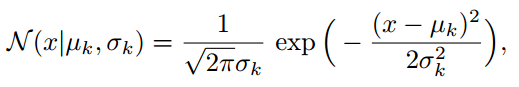
其中 µk 和 σk 分别为第 k 个高斯分布的均值和方差。
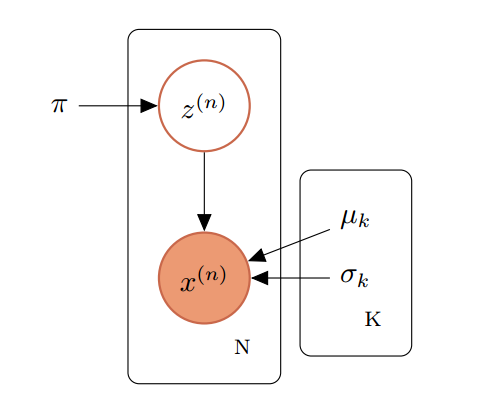
高斯混合模型 的图表示
高斯混合模型的概率密度函数为
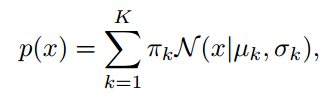

高斯混合模型的生成过程可以分为两步:
- 1. 首先按 π1, π2, · · · , πK 的分布,随机选取一个高斯分布(抽取的样本满足权重系数的分布);
- 2. 假设选中第 k 个高斯分布,再从高斯分布 N (x|µk, σk)中选取一个样本 x。
参数估计
给定 N 个由高斯混合模型生成的训练样本 x(1), x(2), · · · , x(N),希望能学习其中的参数πk, µk, σk, 1 ≤ k ≤ K。由于我们无法观测样本x(n) 是从哪个高斯分布生成的,因此无法直接用最大似然来进行参数估计(含有隐变量)。我们引入一个隐变量z(n) ∈ [1, K]来表示其来自于哪个高斯分布, z(n) 服从多项分布,其多项分布的参数为 π1, π2, · · · , πK,即

对每个样本 x(n),其对数边际分布为

根据 EM算法,参数估计可以分为两步进行迭代:



高斯混合模型的参数学习过程

给定一组数据,假设我们用两个高斯分布来估计这组数据的分布情况。
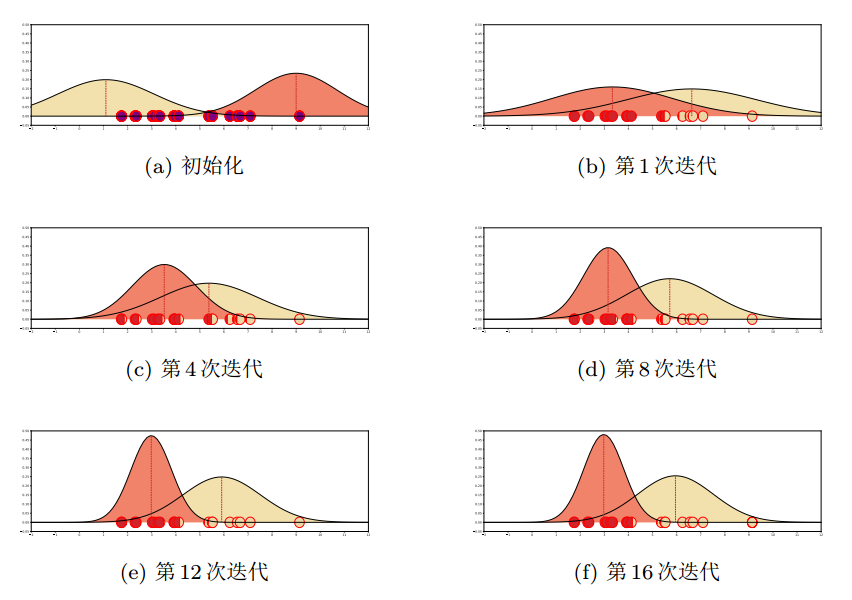
代码实现:待补充???