标准化
概念
- 定义:通过对原始数据进行变换把数据变换到均值为0,标准差为1范围內
- 公式
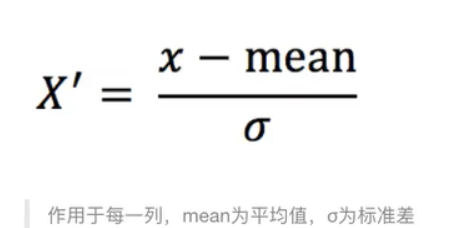
-
示例:


-
优缺点:使得某一个特征对最终结果不对造成更大的影响;对于异常点处理不好,容易影响最大值最小值,鲁棒性较差(稳定性),只适合精确小数据场景
代码
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from matplotlib import gridspec
import numpy as np
import matplotlib.pyplot as plt
#构建数100行、2列的数据集
cps = np.random.random_integers(0, 100, (100, 2))
#实例化一个转换器
ss = StandardScaler()
#调用fit_transform
std_cps = ss.fit_transform(cps)
#绘图
gs = gridspec.GridSpec(5,5)
fig = plt.figure()
ax1 = fig.add_subplot(gs[0:2, 1:4])
ax2 = fig.add_subplot(gs[3:5, 1:4])
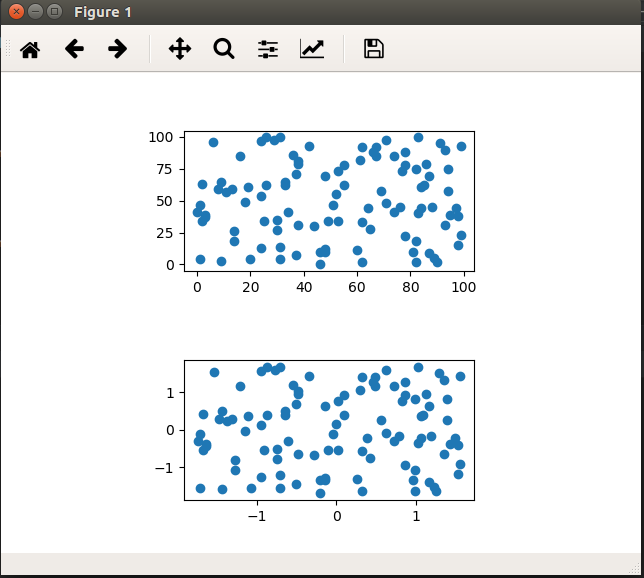
#展示原始数据散点图
ax1.scatter(cps[:, 0], cps[:, 1])
#展示标准化后的散点图,两者分布几乎一致
ax2.scatter(std_cps[:, 0], std_cps[:, 1])
plt.show()
运行截图
归一化
概念
-
定义:通过对原始数据进行变换把数据映射到(默认为[0,1])之间
-
公式:
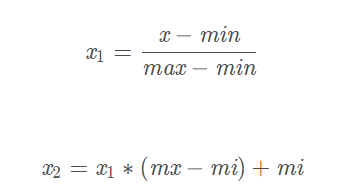
-
示例:
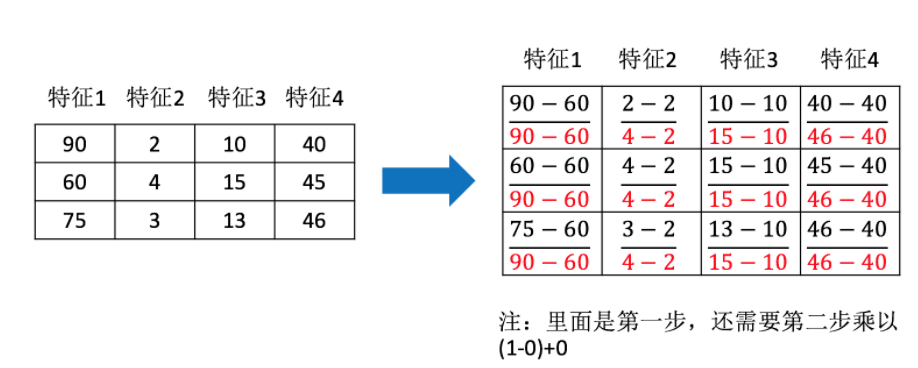
-
优缺点:由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小
代码
from sklearn.preprocessing import MinMaxScaler
import numpy as np
#构建10行、1列的数据集
data = np.random.uniform(0, 100, 10)[:, np.newaxis]
#实例化一个转换器
mm = MinMaxScaler()
#调用fit_transform,获取归一化后的数据
mm_data = mm.fit_transform(data)
#获取归一化后的数据转换为原始数据
origin_data = mm.inverse_transform(mm_data)
print('data is ',data)#原始数据
print('after Min Max ',mm_data)#归一化后数据(分布在(0,1)之间)
print('origin data is ',origin_data)#将归一化数据转换为原始数据
运行截图

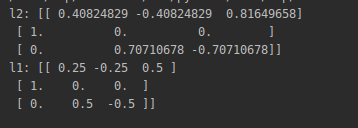
正则化
代码
X = [[1, -1, 2],
[2, 0, 0],
[0, 1, -1]]
# 使用L2正则化
from sklearn.preprocessing import normalize
l2 = normalize(X, norm='l2')
print('l2:', l2)
# 使用L1正则化
from sklearn.preprocessing import Normalizer
normalizerl1 = Normalizer(norm='l1')
l1 = normalizerl1.fit_transform(X)
print('l1:', l1)
运行截图